David Dumas and Michael Wolf

A key object of study in our work is a cubic form on the tangent bundle of the affine sphere, known as the Pick form. One way to think about the Pick form is that it measures the difference between notions of geodesic for two natural connections on the surface—the restriction of the flat connection of R3, and the Levi-Civita connection of a metric on the surface constructed from its Hessian.
For an affine sphere over a convex n-gon, we show that the Pick form vanishes at exactly (n-3) points—the Pick zeros. This set of Pick zeros is a projective invariant of the polygon.
We wondered whether anything about the arrangement of the Pick zeros could be understood directly in terms of projective geometry of the polygon, without referring to constructions in affine differential geometry.
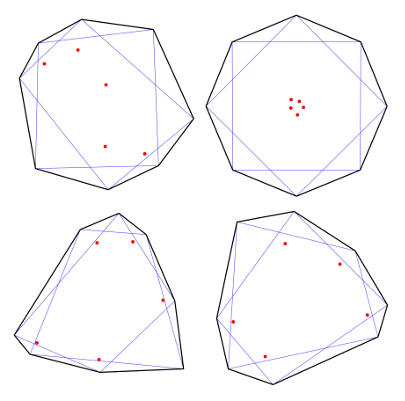
In a series of computer experiments (see software below) we noticed that the Pick zeros seem to "avoid" certain parts of the polygon. To make this precise, consider the triangles formed by triples of consecutive vertices of a convex n-gon. Cutting all of these away leaves a smaller n-gon, which we call the fence of P. In some cases the fence degenerates to a point, as in a regular polygon, or to a line segment. Our experiments suggest the following:
Conjecture: For any convex n-gon in RP2, the Pick zeros lie inside the fence.The image above shows a few examples: The five marked points (in red) in each octagon are the Pick zeros. The diagonals of each octagon which we cut along to get the fence are shown in blue, so the fence itself is the smaller octagon formed from the blue edges.
The animations are hosted on YouTube for convenient online viewing. Higher-quality MP4 video files are also available for download.

This family of octagons corresponds to polynomials with roots moving along five circles in the complex plane. Each circle contains the origin and one of the fifth roots of unity. The roots move around the circles at different rates, resuling in a family that visits various parts of the moduli space. The animation starts and ends with the regular octagon, corresponding to the polynomial z5.
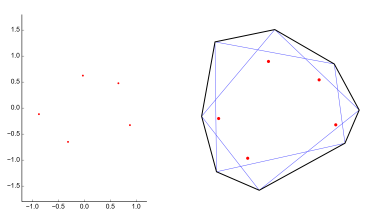
This variation on the previous animation shows side-by-side views of the zeros of the complex polynomial and the corresponding polygon with its Pick zeros.
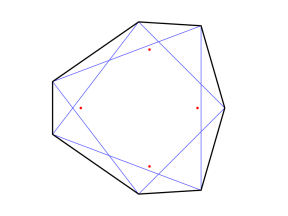
This family of heptagons corresponds to polynomials of the form (z4 - c) with the complex constant c starting at the origin, moving through positive real values, and then rotating along the unit circle. In the corresponding heptagons, the Pick zeros appear to approach and then march along the fence, turning corners as necessary.

This variation on the previous animation shows side-by-side views of the zeros of the complex polynomial and the corresponding polygon with its Pick zeros.