Formats of polynomial systems

A complex polynomial system 

is denoted by the dimension  followed by as many complex multivariate polynomials as the dimension. The dimension is a positive natural number.

A complex multivariate polynomial 

is denoted as a sequence of terms, separated by + and terminated by the semicolon ;. The brackets ( and ) must be used to isolate a sequence of terms as a factor in a complex multivariate polynomial.

A term 

can be either a coefficient or a coefficient, followed by * and a monomial. If in the latter case the coefficient equals one, then it may be omitted.

A coefficient 

may be denoted as an integer, a rational, a floating-point or a complex number.

A monomial 

is a sequence of powers of unknowns, separated by *. The power  operator is represented by ** or 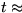$\hat{~}$.It must be followed by a positive natural number. If the power equals one, then it may be omitted.

An unknown 

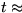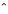can be denoted by at most five characters. The first character must be a letter and the other two characters must be different from +, -, *, $\hat{~}$, /, ;, ( and ). The letter i means $\sqrt{-1}$, whence it does not represent an unknown. The number of unknowns may not exceed the declared dimension.

Some examples of valid notations of complex multivariate polynomials:

  x**2*y + 1/2*z*y**2 - 2*z + y**3 + x - 1E9/-8.E-6* y + 3;
  x^2*y + z*y^2 - 2*z + y^3 + x - y + 3;
  (1.01 + 2.8*i)*x1**2*x2 + x3**2*x1 - 3*x1 + 2*x2*x3 - 3;
  (x1^2*x2 + x3^2*x1 - 3*x1 + 2*x2*x3 - 3)*x2**2*(x2-1+i);

Some notes concerning the internal representation:

• Graded lexicographical ordering is used for the monomials.
• The internal order of the unknowns is determined by the order in which they occur in the polynomial system. For example, if x2 is read before x1, then the powers of x2 will come first in the representation of the support sets and mixed subdivision.
• The continuation parameter is represented by t. Although t is not a reserved symbol, it is better not to use it to represent unknowns, to avoid confusion.

An input file to phc must begin with a polynomial system in the appropriate format. As example, consider the intersection of a circle with a parabola:

2
 x**2 + 4*y**2 - 4;
        2*y**2 - x;