Trees

A tree is a recursive data structure. We consider a binary tree to sort a sequence of numbers.

Binary Trees

Consider the sequence 4, 5, 2, 3, 8, 1, 7. The problem is to sort the sequence in increasing order. Insert the numbers in a tree, as shown in Fig. 35.

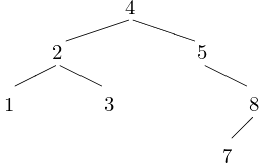
Fig. 35 A binary tree stores a sorted sequence of numbers.

The rules to insert the value \(x\) at the node \(N\) are the following:

• If \(N\) is empty, then put \(x\) in \(N\).
• If \(x < N\), insert \(x\) to the left of \(N\).
• If \(x \geq N\), insert \(x\) to the right of \(N\).

Consider the printing of the tree in a recursive manner. At any node, we print the left branch (if not empty) first, then we print the value at the node, and lastly, we print the right branch (if not empty). Walking through the tree in this fashion will print the numbers in increasing order.

Any node in a tree T of numbers is either empty or consists of

1. The left branch (or child) is a tree.
2. The data at the node is a number.
3. The right branch (or child) is a tree.

To represent a tree as shown in Fig. 36 we can use recursive triplets.

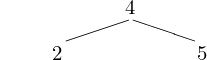
Fig. 36 An example of a binary tree.

We use tuples, sequences enclosed by ( and ):

>>> L = ((),2,())
>>> R = ((), 5, ())
>>> T = (L, 4, R)
>>> T
(((), 2, ()), 4, ((), 5, ()))

Using nested tuples to represent binary trees, we can provide code for the tree sort. The session below illustrates the development of the tree.

$ python treesort.py
give a number (-1 to stop) : 4
T = ((), 4, ())
give number (-1 to stop) : 5
T = ((), 4, ((), 5, ()))
give number (-1 to stop) : 2
T = (((), 2, ()), 4, ((), 5, ()))
give number (-1 to stop) : 3
T = (((), 2, ((), 3, ())), 4, ((), 5, ()))
give number (-1 to stop) : 8
T = (((), 2, ((), 3, ())), 4, ((), 5, ((), 8, ())))
give number (-1 to stop) : -1
sorted numbers = [2, 3, 4, 5, 8]

The function below implements the rules (formulated earlier) to insert a number to a node in a tree.

def add(tree, nbr):
    """
    Adds a number nbr to the triple of triples.
    All numbers less than tree[1] are in tree[0].
    All numbers greater than or equal to tree[1]
    are in tree[2].  Returns the new tree.
    """
    if len(tree) == 0:
        return ((), nbr, ())
    elif nbr < tree[1]:
        return (add(tree[0], nbr), tree[1], tree[2])
    else:
        return (tree[0], tree[1], add(tree[2], nbr))

Consider for example the tree T

(((), 2, ((), 3, ())), 4, ((), 5, ((), 8, ())))

and we see that T already orders the numbers increasingly. The list of nummbers correspodning to T is

L = [2, 3, 4, 5, 8].

To flatten the tree T into the list L, we traverse T as follows:

• If the node is empty, return [].

• For a node that is not empty:

  1. let L be the flattened left branch,
  2. append to L the data at the node,
  3. append to L the flattened right branch,

  and finally return the list L.

Suppose we do not wish to store duplicate elements. To see whether a number n already belongs to a tree T we apply the following recursive algorithm:

• If T is empty, we return False (first base case).
• If the data at the node is n, return True (second base case).
• If n is less then the data at T, return the result of search in left branch otherwise return result of search in right branch.

The algorithm is implemented in the function below.

def is_in(tree, nbr):
    """
    Returns True if nbr belongs to the tree,
    returns False otherwise.
    """
    if len(tree) == 0:
        return False
    elif tree[1] == nbr:
        return True
    elif nbr < tree[1]:
        return is_in(tree[0], nbr)
    else:
        return is_in(tree[2], nbr)

The function to flatten a tree into a list is defined below.

def flatten(tree):
    """
    tree is a recursive triple of triplets.
    Returns a list of all numbers in tree
    going first along the left of tree, before
    the data at the node and the right of tree.
    """
    if len(tree) == 0:
        return []
    else:
        result = flatten(tree[0])
        result.append(tree[1])
        result = result + flatten(tree[2])
        return result

At last, the main function follows.

def main():
    """
    Prompts the user for numbers and sorts
    using a tree: a triple of triplets.
    """
    tree = ()
    while True:
        nbr = int(input('give a number (-1 to stop) : '))
        if nbr < 0:
            break
        if is_in(tree, nbr):
            print(nbr, 'is already in the tree')
        else:
            tree = add(tree, nbr)
        print('T =', tree)
    print('sorted numbers =', flatten(tree))

Classification Trees

To build trees with a variable number of children at each node we can use lists instead of tuples. A more flexible indexing mechanism is provided by dictionaries. For example, a mileage table to store distances from Chicago to Miami, Los Angeles and New York:

>>> mt = { 'Miami':1237 , 'LA':2047 , 'NY':807 }
>>> mt['LA']
2047
>>> list(mt.keys())
['Miami', 'NY', 'LA']
>>> list(mt.values())
[1237, 807, 2047]

A dictionary is a set of key:value pairs.

Suppose we want to classify animals with simple questions with yes or no answers. An example is shown in Fig. 37.

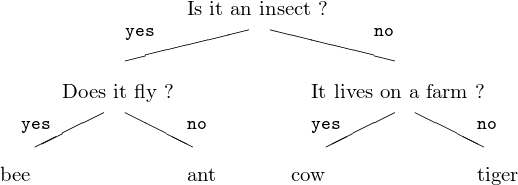
Fig. 37 Classifying animals with yes or no questions.

The leaves of the tree are just strings. The internal nodes have questions as strings, and yes and no branches leading to more questions or to the names of the animals.

An example run with the script to build a classification tree follows.

$ python3 treezoo.py
What animal ? tiger
d = ['tiger']
continue ? (y/n) y
Is it "tiger" ? (y/n) n
What animal ? ant
Give question to distinguish "ant" from "tiger":
Is it an insect ?

The resulting dictionary is then

d = {‘q’: ‘Is it an insect ?’, ‘y’: [‘ant’], ‘n’: [‘tiger’]}

The classification tree is defined as follows:

• Leaves in the tree are lists of one string.
• An internal node contains three keys: for the question, the yes and the no answer.

The script treezoo.py continues after the construction with the navigation.

ended construction, start navigation...
Is it an insect ? (y/n) y
Does it fly ? (y/n) y
arrived at "bee"

The answer of the user y or n is the key to the branches of the tree.

The rules in the navigation algorithm are:

• We are in the base case if the length of the dictionary is one.
• In the general case, follow the answer of the user.

The navigation algorithm is implemented by the navigate() function.

def navigate(dic):
    """
    Navigates through the dictionary dic
    based on the user responses.
    """
    if len(dic) == 1:
        print('arrived at \"' + dic[0] + '\"')
    elif len(dic) == 3:
        ans = input(dic['q'] + ' (y/n) ')
        navigate(dic[ans])

Consider the addition of elements to the tree. We have two base cases:

• For an empty tree, we ask for the animal name.
• At a leaf, we ask if it is the animal
  • if yes, then we are done, otherwise
  • if no, we ask the name of the new animal and a question to distinguish it from the others.

In the general case, we ask the question at the node and make a recursive call, adding to the branch y or n. The code is listed in the function below.

def add(dic):
    """
    Adds a new element to the dictionary dic,
    via interactive questions to the user.
    """
    if len(dic) == 0:
        ans = input('What animal ? ')
        return [ans]
    elif len(dic) == 1:
        qst = 'Is it \"' + dic[0] + '\" ? (y/n) '
        ans = input(qst)
        if ans == 'y':
            print('okay, got it')
            return dic
        else:
            ans = input('What animal ? ')
            ask = 'Give question to distinguish \"' + \
                 ans + '\" from \"' + dic[0] + '\":\n'
            qst = input(ask)
            return {'q':qst, 'y':[ans], 'n':[dic[0]]}
    else:
        ans = input(dic['q'] + ' (y/n) ')
        if ans == 'y':
            return {'q':dic['q'], 'y':add(dic['y']), 'n':dic['n']}
        else:
            return {'q':dic['q'], 'y':dic['y'], 'n':add(dic['n'])}

The main function follows.

def main():
    """
    Builds interactively a tree to classify animals.
    """
    zoo = {}
    while True:
        zoo = add(zoo)
        print('zoo =', zoo)
        ans = input("continue ? (y/n) ")
        if ans != 'y':
            break
    print('ended construction, start navigation...')
    while True:
        navigate(zoo)
        ans = input("continue ? (y/n) ")
        if ans != 'y':
            break

Exercises

1. Use the code add, flatten, and is_in as methods in a class to represent trees to sort numbers.
2. Modify the representation of the tree to sort numbers, using a dictionary instead of a triplet. As keys use the strings 'data', 'smaller', and 'larger'. The leaves of the tree have only one element: 'data':number.
3. For the tree of dictionaries to classify animals, write a function which takes on input the tree and returns the list of all animal names in the tree.
4. Use dbm to store the tree of dictionaries to classify animals. Note that dbm requires all keys and values to be of type string.