Divide and Conquer

We can search fast through huge sort data via the divide and conquer search method.

Guessing a Secret

Consider the following little game:

• The computer picks a random integer in [0, 1000].
• It is up to the user to guess the number.

Suppose making a guess costs $1 and you get $100 for the right guess. Would you play this game?

Suppose now the computer would tell you after each incorrect guess: too low or too high. With same cost and price, would you now play this game?

An example of a session of the game with the too low and too high feedback is shown below.

$ python findsecret.py
Guess number in [0, 1000] : 500
Your guess is too low.
Guess number in [0, 1000] : 750
Your guess is too high.
Guess number in [0, 1000] : 625
Your guess is too high.
Guess number in [0, 1000] : 562
Your guess is too high.
Guess number in [0, 1000] : 531
Your guess is too high.
Guess number in [0, 1000] : 516
Your guess is too high.
Guess number in [0, 1000] : 508
Your guess is too high.
Guess number in [0, 1000] : 504
Your guess is too low.
Guess number in [0, 1000] : 506
found 506 after 9 guesses

The search space is [0, 1000] at the start, in Fig. 38.

Fig. 38 Halving the search space in each step.

As shown in Fig. 38, in each step the search space is cut in half. After 10 steps, we are down to the last digit. In every step we recover one bit of the secret.

Binary Search

Let us generate a list of 10 random two digit numbers. Consider the session below.

>>> from random import randint
>>> L = [randint(10, 99) for _ in range(10)]
>>> L
[32, 61, 50, 81, 30, 14, 53, 92, 22, 23]
>>> 10 in L
False
>>> 81 in L
True
>>> L.index(81)
3
>>> L[3]
81

The instruction L.index(n) will throw a ValueError if n not in L.

The formulation of the input/output of the search problem is below:

\[\begin{split}\begin{array}{rcl} Input & : & \mbox{\tt L} \mbox{ a list of numbers and some number } \mbox {\tt x}. \\ Output & : & \mbox{index } \mbox{\tt k == -1}, \mbox{if } \mbox{\tt not x in L} \mbox{ otherwise } \mbox{\tt L[k] == x}. \end{array}\end{split}\]

The algorithm for a linear search executes the following steps:

1. Enumerate in L all its elements in L[k].
2. If L[k] == x then return k.
3. Return -1 at the end of the loop.

Our cost analysis first considers the best case. In the best case, we find x immediately if x occurs at the start of L. In the worst case, we have to traverse the entire list if x is at the end of L. On average, we execute \(c \times n\) steps, where \(n =~\) len(L), for some constant \(c \approx 0.5\). We say its cost is \(O(n)\).

Code to search linearly in a sorted list is below. To sort a list L, do L.sort().

def linear_search(numbers, nbr):
    """
    Returns -1 if nbr belongs to numbers,
    else returns k for which numbers[k] == nbr.
    Items in the list numbers must be sorted
    in increasing order.
    """
    for i in range(len(numbers)):
        if numbers[i] == nbr:
            return i
        elif numbers[i] > nbr:
            return -1
    return -1

The builtin in and index for lists do not exploit order.

The problem statement to search in a sorted list is below.

\[\begin{split}\begin{array}{rcl} Input & : & \mbox{\tt L} \mbox{ is a list of numbers, ordered increasingly;} \mbox{\tt x} \mbox{ is some number.} \\ Output & : & \mbox{\tt True} \mbox{ if } \mbox{\tt x in L}, \mbox{\tt False} \mbox{ otherwise.} \end{array}\end{split}\]

The rules to apply divide and conquer are

• The base cases are len(L) == 0 and len(L) == 1.
• Let m = len(L)//2. If L[m] == x, then return True.
• If x < L[m], then search in the first half of L, that is L[:m].
• If x > L[m], then search in the second half of L, that is L[m+1:].

Code for a binary search is in the function below.

def binary_search(numbers, nbr):
    """
    Returns True if nbr is in the sorted numbers.
    Otherwise False is returned.
    """
    if len(numbers) == 0:
        return False
    elif len(numbers) == 1:
        return numbers[0] == nbr
    else:
        middle = len(numbers)//2
        if numbers[middle] == nbr:
            return True
        elif numbers[middle] > nbr:
            return binary_search(numbers[:middle], nbr)
        else:
            return binary_search(numbers[middle+1:], nbr)

We trace the search by * accumulating the depth of the recursion, * printing as many spaces as the depth, * printing the remaining list to search in.

To test the search, we generate a list of random 2-digit numbers.

Give lower bound : 10
Give upper bound : 99
How many numbers ? 10
L = [10, 14, 14, 19, 20, 38, 53, 60, 66, 72]
Give number to search for : 21
find 21 in L = [10, 14, 14, 19, 20, 38, 53, 60, 66, 72]
 find 21 in L = [10, 14, 14, 19, 20]
  find 21 in L = [19, 20]
   find 21 in L = []
21 does not occur in L

The builtin index does not exploit order either. Let us define an index search for sorted lists.

def binary_index(numbers, nbr):
    """
    Applies binary search to find the
    position k of nbr in the sorted numbers.
    Returns -1 if not nbr in numbers, or else
    returns k for which numbers[k] == nbr.
    """

We apply the same divide and conquer as in binary_search(), with additional attention to the index calculation.

Code to define the binary_index(numbers, nbr) function follows.

# search for the index of nbr in a sorted list numbers
    if len(numbers) == 0:
        return -1
    elif len(numbers) == 1:
        return (0 if numbers[0] == nbr else -1)
    else:
        middle = len(numbers)//2
        if numbers[middle] == nbr:
            return middle
        elif numbers[middle] > nbr:
            return binary_index(numbers[:middle], nbr)
        else:
            k = binary_index(numbers[middle+1:], nbr)
            if k == -1:
                return -1
            return k + middle + 1

Bisection Search

A related problem to binary search is bisection search, used to invert a function. Consider a cumulative distribution function, for example, as shown in Fig. 39.

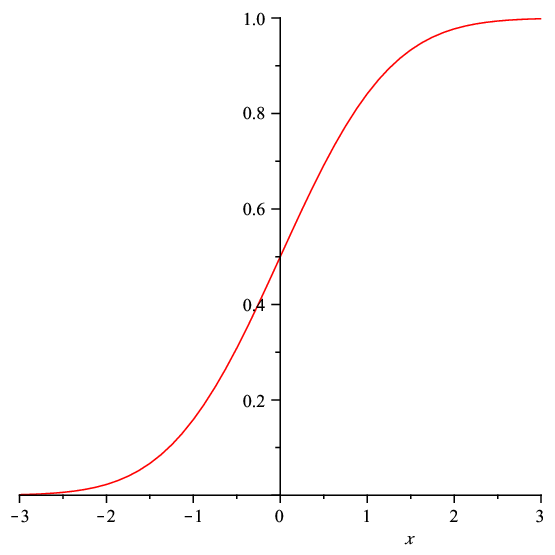
Fig. 39 Inverting a function: given $y = f(x)$, find $x$.

The problem statement of inverting a sampled function is below.

\[\begin{split}\begin{array}{rcl} Input & \mbox{1.} & \mbox{a sampled array } A \mbox{ of function values,} \\ & \mbox{2.} & \mbox{a particular function value } y = f(x). \\ Output & k: & A[k] \leq y \leq A[k+1]. \end{array}\end{split}\]

We work with arrays of numbers sorted in increasing order. Consider the interactive Python session below.

>>> from random import uniform as u
>>> L = [u(-1, 1) for _ in range(10)]
>>> L.sort()
>>> from array import array
>>> A = array('d', L)

A linear search is provided in the function below.

def linear_search(arr, nbr):
    """
    Returns the index k in the array arr
    such that arr[k] <= nbr <= arr[k+1].
    A must be sorted in increasing order.
    """
    for i in range(len(arr)):
        if nbr <= arr[i]:
            return i-1
    return len(arr)

The bisection search in an array uses a function with the following prototype.

def bisect_search(arr, nbr):
    """
    Returns the index k in the array arr such that
    arr[k] <= nbr <= arr[k+1] applying binary search.
    """

We have two base cases:

1. If len(arr) == 0, then return -1.
2. If len(arr) == 1, then return 0 if arr[0] <= nbr, otherwise return -1.

In the general case, define m = len(arr)//2.

1. If nbr < arr[m], then search in arr[:m].
2. If nbr > arr[m], then search in arr[m+1:]. Add m+1 to the index returned by 2nd search.

The code for the recursive function is below.

def bisect_search(arr, nbr):
    """
    Returns the index k in the array arr such that
    arr[k] <= nbr <= arr[k+1] applying binary search.
    """
    if len(arr) == 0:
        return -1
    elif len(arr) == 1:
        if arr[0] <= nbr:
            return 0
        else:
            return -1
    else:
        middle = len(arr)//2
        if nbr < arr[middle]:
            return bisect_search(arr[:middle], nbr)
        else:
            k = bisect_search(arr[middle+1:], nbr)
            return k + middle +1

An application of the bisection search is the root finding problem.

Let f be a continuous function over \([a,b]\), and \(f(a) f(b) < 0\), then \(f(r) = 0\), for some \(r \in [a,b]\).

The key steps in the bisection method are the following.

1. Let \(m = \frac{a+b}{2}\).
2. If \(f(a) f(m) < 0\), then replace \([a,b]\) by \([a,m]\), otherwise replace \([a,b]\) by \([m,b]\).

Every step gains one bit in an approximate root r of f. The function bisect() does one step of the bisection method:

def bisect(fun, left, right):
    """
    If (left, right) contains a root of fun,
    then on return is a smaller (left, right)
    containing a root of fun.
    """
    midpoint = (left + right)/2
    if fun(left)*fun(midpoint) < 0:
        return (left, midpoint)
    else:
        return (midpoint, right)

The accuracy of the root is right - left. Let tol be the tolerance on the error on the root. If right - left < tol, return (left, right) else call bisect again. This recursive bisection method is defined below.

def bisectroot(fun, left, right, tol):
    """
    Continues bisecting till the right - left
    is less than tol.
    """
    if right-left < tol:
        return (left, right)
    else:
        (left, right) = bisect(fun, left, right)
        return bisectroot(fun, left, right, tol)

As an example, consider the approximation of \(\sqrt{2}\).

$ python bisection.py
Give a function in x : x**2 - 2
give left bound A : 1
give right bound B : 2
give the tolerance : 1.0e-12
A =  1.4142135623724243
B =  1.4142135623733338
$

Exercises

1. Write an iterative version of binary_search.
2. Write an iterative version of bisectroot.
3. The minimum of a list of unsorted numbers is the minimum of the minimum of the first half and the minimum of the second half of the list. Write a function to compute the minimum this way.
4. Given is a list of lexicographically sorted names. Use divide and conquer to find the name that occurs most frequently in the list.
5. Develop bisection search to compute the binary representation of a number x, starting at the most significant bit. Use math.log(x,2) to compute the total number of bits needed to represent x.