From Recursion To Iteration

Quicksort Revisited

Recall the idea of Quicksort on a list:

1. Choose \(x\) and partition list in two: left list: \(\leq x\) and right list: \(> x\).
2. Sort the left and right lists.

An implementation with the buildin lists of Python is recursively functional. This implementation is convenient, but requires multiple copies of the same data. Arrays are a more efficient data structure. To sort in place, we turn the recursion into an iteration.

To test our code, we generate an array of random integers.

from array import array as Array

def main():
    """
    Generates a random array of integers
    and applies quicksort.
    """
    low = int(input('Give lower bound : '))
    upp = int(input('Give upper bound : '))
    nbr = int(input('How many numbers ? '))
    ans = input('Extra output ? (y/n) ')
    from random import randint
    nums = [randint(low, upp) for _ in range(nbr)]
    data = Array('i', nums)
    print('A =', data)
    recursive_quicksort(data, 0, nbr, ans == 'y')
    print('A =', data)

Take x in the middle of the array. Partial pseudo code to swap elements is below.

for all i < j:
    if A[i] > x and A[j] < i: (A[i], A[j]) = (A[j], A[i])

Consider for example: A = [31 93 49 37 56 95 74 59] At the middle: x = 56 == A[4]. We start with i = 0 and j = 8 and then do the following.

• Increase i while A[i] < x. This ends at i=1.
• Decrease j while A[j] > x. This ends at j=4.

Swap A[1] and A[4], and then continue scanning A for swaps.

A = [31 93 49 37 56 95 74 59]
i = 4, j = 3, x = 56
A[0:4] = [31 56 49 37] <= 56
A[4:8] = [93 95 74 59] >= 56

The function partition() defines the partitioning of an array.

def partition(arr, first, last):
    """
    Partitions arr[first:last] using as pivot
    the middle item x.  On return is (i, j, x):
    i > j, all items in arr[i:last] are >= x,
    all items in arr[first:j+1] are <= x.
    """
    pivot = arr[(first+last)//2]
    i = first
    j = last-1
    while i <= j:
        while arr[i] < pivot:
            i = i+1
        while arr[j] > pivot:
            j = j-1
        if i < j:
            (arr[i], arr[j]) = (arr[j], arr[i])
        if i <= j:
            (i, j) = (i+1, j-1)
    return (i, j, pivot)

To verify the correctness we check postconditions. Consider the same example from above.

i = 4, j = 3, x = 56
A[0:4] = [31 56 49 37] <= 56
A[4:8] = [93 95 74 59] >= 56

This check is performed in general by the following function.

def check_partition(arr, first, last, i, j, pivot):
    """
    Prints the result of the partition
    for a visible check on the postconditions.
    """
    print('i = %d, j = %d, x = %d' % (i, j, pivot))
    print('arr[%d:%d] =' % (first, j+1), \
        arr[first:j+1], '<=', pivot)
    print('arr[%d:%d] =' % (i, last), \
        arr[i:last], '>=', pivot)

The partition() function is applied at the start of a recursive quick sort function.

def recursive_quicksort(data, first, last, verbose=True):
    """
    Sorts the array data in increasing order.
    If verbose, then extra output is written.
    """
    (i, j, pivot) = partition(data, first, last)
    if verbose:
        check_partition(data, first, last, i, j, pivot)
    if j > first:
        recursive_quicksort(data, first, j+1, verbose)
    if i < last-1:
        recursive_quicksort(data, i, last, verbose)

Notice that data[first:j+1] is sorted first.

Converting Recursion into Iteration

Recursion is executed via a stack. For quicksort, we store first and last index of the array to sort. With every call we push (first, last) on the stack. As long as the stack of indices is not empty:

1. Pop the indices (first, last) from the stack.
2. We partition the array A[first:last].
3. Push (i, last) and then (first, j+1).

The iterative version of the quicksort runs as follows. Observe the evoluation of the stack S of indices.

A = [31 93 49 37 56 95 74 59]
S = [(0, 8)]
i = 4, j = 3, x = 56
A[0:4] = [31 56 49 37] <= 56
A[4:8] = [93 95 74 59] >= 56
S = [(0, 4), (4, 8)]
i = 3, j = 1, x = 49
A[0:2] = [31 37] <= 49
A[3:4] = [56] >= 49
S = [(0, 2), (4, 8)]
i = 2, j = 0, x = 37
A[0:1] = [31] <= 37
A[2:2] = [] >= 37
S = [(4, 8)]
...

Code an iterative quicksort is given in the function below.

def iterative_quicksort(nbrs, verbose=True):
    """
    The iterative version of quicksort
    uses a stack of indices in nbrs.
    """
    stk = []
    stk.insert(0, (0, len(nbrs)))
    while stk != []:
        if verbose:
            print('S =', stk)
        (first, last) = stk.pop(0)
        (i, j, pivot) = partition(nbrs, first, last)
        if verbose:
            check_partition(nbrs, first, last, i, j, pivot)
        if i < last-1:
            stk.insert(0, (i, last))
        if j > first:
            stk.insert(0, (first, j+1))

Inverting Control in a Loop

Consider the development of a GUI for the towers of Hanoi puzzle. The problem is to move a pile of disks. In moving a pile from peg A to B, no larger disk may be placed on top of a smaller disk. To obey this rule we may use peg C as an intermediary location to place a disk.

The start configuration is shown in Fig. 40.

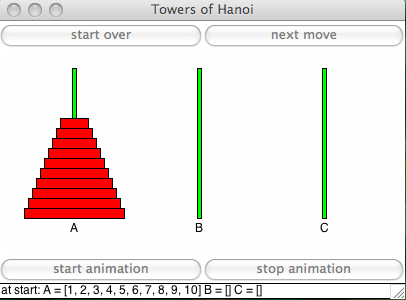
Fig. 40 The start configuration of the GUI.

At the middle, we may have a configuration as shown in Fig. 41.

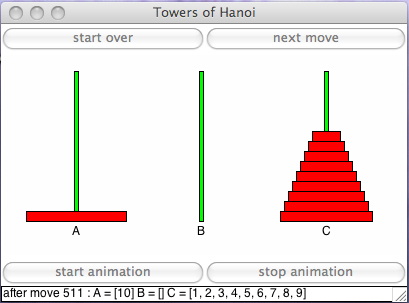
Fig. 41 A configuration in the middle of moving the pile of disks.

The last move is shown in Fig. 42.

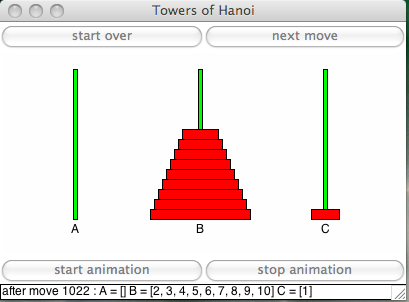
Fig. 42 The last move in solving the towers of Hanoi puzzle.

Recall that a GUI is just an interface to a program. Therefore, we will keep the solution to the puzzle in a separate script. In the development of the GUI, we are primarily concerned with the display of the solution to the puzzle, not with the solution itself.

What is the solution? We need a get_next_move() function. Such a function inverts the control in a loop from the producer to the consumer of the data. Consider the following pseudo code:

def f(n):
    if n == 0:       # base case
       write result
    else:
       recursive call(s)

The recursive function f() controls the calls to write result. If we had a get_next(), then we could write our code as

while True:
    result = get_next();
    if no result: break
    write result

In the original recursive design, the function f() controls the pace of the writing. If we have a get_next() function, then the pace of the writing controls the computation. In other words, we will compute only when a result is needed for writing.

To revert the control of a recursive function, we need a stack. The get_next() function

1. stores all current values of variables and parameters before returning to the caller, and
2. when called again, restores all values.

For the towers of Hanoi we will first convert to an iterative solution, and then adjust to an inverted function. Our data structures are tuples of strings and lists:

::

A = (‘A’,range(1,n+1)) B = (‘B’,[]) C = (‘C’,[])

Recall the recursive solution.

def hanoi(nbr, apl, bpl, cpl, k, move):
    """
    Moves nbr disks from apl to bpl, cpl is auxiliary.
    The recursion depth is counted by k,
    move counts the number of moves.
    Writes the state of the piles after each move.
    Returns the number of moves.
    """
    if nbr == 1:
        # move disk from A to B
        bpl[1].insert(0, apl[1].pop(0))
        write(k, move+1, nbr, apl, bpl, cpl)
        return move+1
    else:
        # move nbr-1 disks from A to C, B is auxiliary
        move = hanoi(nbr-1, apl, cpl, bpl, k+1, move)
        # move nbr-th disk from A to B
        bpl[1].insert(0, apl[1].pop(0))
        write(k, move+1, nbr, apl, bpl, cpl)
        # move nbr-1 disks from C to B, A is auxiliary
        move = hanoi(nbr-1, cpl, bpl, apl, k+1, move+1)
        return move

In an iterative solution for the towers of Hanoi, we use a stack of arguments of function calls:

stk = [(n, 'A', 'B', 'C', k)] # symbols on the stack
while len(stk) > 0:
    top = stk.pop(0)

The recursive code in pseudo code is

if n == 1:
    move disk from A to B
else:
    move n-1 disks from A to C, B is auxiliary
    move n-th disk from A to B
    move n-1 disks from C to B, A is auxiliary

Not only arguments of function calls go on the stack! Observe that B[1].insert(0,A[1].pop(0)) is performed in both the base case and the general case. In all cases, we move a disk from A to B, but only in the base case can we execute directly, in the general case we must store the move. A move is stores as a string on the stack:

top = stk.pop(0)
if isinstance(top, str):
    eval(top)

The move is stored as B[1].insert(0,A[1].pop(0)) and is ready for execution, triggered by eval()

Now we are ready to formulate the interative version of solving the puzzle of the towers of Hanoi.

def iterative_hanoi(nbr, A, B, C, k):
    """
    The iterative version uses a stack of function calls.
    On the stack are symbols for the piles,
    not the actual piles!
    """
    stk = [(nbr, 'A', 'B', 'C', k)]
    cnt = 0
    while len(stk) > 0:
        top = stk.pop(0)
        if isinstance(top, str):
            eval(top)
            if top[0] != 'w':
                cnt = cnt + 1  # a move, not a write
        else:
            (nbr, sa, sb, sc, k) = top
            move = sb + '[1].insert(0,' + sa + '[1].pop(0))'
            if nbr == 1:
                # move disk from A to B
                eval(move)
                cnt = cnt + 1
                write(k, cnt, nbr, A, B, C)
            else: # observe that we swap the order of moves!
                # move nbr-1 disks from C to B, A is auxiliary
                stk.insert(0, (nbr-1, sc, sb, sa, k+1))
                # move nbr-th disk from A to B
                stk.insert(0, ("write(%d,cnt,%d,A,B,C)" % (k, nbr)))
                stk.insert(0, move)
                # move nbr-1 disks from A to C, B is auxiliary
                stk.insert(0, (nbr-1, sa, sc, sb, k+1))

The inverted version of the towers of Hanoi uses the function with prototype:

def get_next_move(stk, A, B, C):
    """
    Computes the next move, changes the stack stk,
    and returns the next move to the calling routine.
    """

The inverted version of the towers of Hanoi is

def inverted_hanoi(nbr, apl, bpl, cpl, k):
    """
    This inverted version of the towers of Hanoi gives
    the control to the writing of the piles.
    """
    stk = [(nbr, 'A', 'B', 'C', k)]
    cnt = 0
    while True:
        move = get_next_move(stk, apl, bpl, cpl)
        if move == '':
            break
        cnt = cnt + 1
        pre = 'after move %d :' % cnt
        write_piles(pre, apl, bpl, cpl)

The complete get_next_move() function is below.

def get_next_move(stk, A, B, C):
    """
    Computes the next move, changes the stack stk,
    and returns the next move to the calling routine.
    """
    while len(stk) > 0:
        top = stk.pop(0)
        if isinstance(top, str):
            eval(top)
            return top
        else:
            (nbr, sap, sbp, scp, k) = top
            move = sbp + '[1].insert(0,' + sap + '[1].pop(0))'
            if nbr == 1:
                eval(move) # move disk from A to B
                return move
            else: # observe that we swap the order of moves!
                # move nbr-1 disks from C to B, A is auxiliary
                stk.insert(0, (nbr-1, scp, sbp, sap, k+1))
                # move nbr-th disk from A to B
                stk.insert(0, move)
                # move nbr-1 disks from A to C, B is auxiliary
                stk.insert(0, (nbr-1, sap, scp, sbp, k+1))
        return ''

The GUI contains nothing new, see the course web site for its code.

Exercises

1. Give Python code to enumerate all permutations of an array without making a copy of the array.
2. Two natural numbers \(m\) and \(n\) are input to the Ackermann function \(A\). For \(m=0\): \(A(0,n) = n+1\), for \(m > 0\): \(A(m,0) = A(m-1,1)\), and for \(m > 0\), \(n > 0\): \(A(m,n) = A(m-1,A(m,n-1))\).
   1. Give a recursive Python function for \(A\).
   2. Turn the recursive function into an iterative one.
3. Write an iterative version of the GUI to draw Hilbert’s space filling curves.