Lecture 40: Computational Group Theory with GAP¶
GAP stands for Groups, Algorithms and Programming.
We can run GAP explicitly in Sage via gap
or open a terminal session with GAP.
There are many groups one can explore with GAP. We start with the permutation groups. As an application, we can apply GAP commands to analyze Rubik’s cube.
Permutation Groups¶
We can define permutation groups via transpositions. For example, to swap 1 with 2, we can define a transposition as follows.
a = gap("(1, 2)")
print(a, 'has type', type(a))
We can convert a GapElement into a Sage element,
but we get just a tuple back, which is not what we may want.
print(a.sage())
print(type(a.sage()))
We see that the
sage.interfaces.gap.GapElement
turns into the type tuple for which no group operations
are defined.
We read (1, 2) as 1 is mapped to 2 and 2 is mapped to 1.
A transposition is its own inverse.
gap('Inverse(%s)' % a)
The way to assign GAP variables in a Sage worksheet is via the set method.
Then we can retrieve the values of the GAP variables with get.
gap.set('a', '(1,2)')
gap.get('a')
Let us check that a is its own inverse:
gap.get('a*a')
and indeed, we see (), which is the identity permutation.
Let us make another transposition, b, and multiply b with a.
gap.set('b', '(1, 3)')
gap.set('c', 'a*b')
gap.get('c')
What is printed for c is (1,2,3).
The cycle notation for c means that 1 is mapped to 2,
2 is mapped to 3, and 3 is mapped to 1.
To verify this notation, consider (x, y, z) and the
application of a: (y, x, z), followed by b: (z, x, y),
so we see that x moved from first to second position,
y from second to third, and z from third to first.
Note that if we first apply (1, 3) to (x, y, z),
we get (z, y , x), followed by (1, 2), then we end up
with (y, z, x), so a*b is not equal to b*a.
We can have GAP generate the group generated by a and b.
gap.set('g', 'Group(a,b)')
gap('g')
Then we see that g corresponds to Group( [ (1,2), (1,3) ] ).
We can list all elements in a group with an enumerator.
print gap('Size(g)')
gap.set('e', 'Enumerator(g)')
e
We see there are six elements in the group. Now we can use the enumerator to list all elements of the group.
gap.set('G', 'List([1..Size(g)], i -> e[i])')
gap.get('G')
The elements in the group are listed as
[ (), (1,2,3), (1,3,2), (2,3), (1,2), (1,3) ].
The multiplication table stores the results of all multiplications for each pair of elements in the group. We see exactly one 1 on every row and every column, so each element in the group has an inverse.
T = gap('MultiplicationTable(G)')
for t in T: print(t)
And the multiplication table is
[ 1, 2, 3, 4, 5, 6 ]
[ 2, 3, 1, 6, 4, 5 ]
[ 3, 1, 2, 5, 6, 4 ]
[ 4, 5, 6, 1, 2, 3 ]
[ 5, 6, 4, 3, 1, 2 ]
[ 6, 4, 5, 2, 3, 1 ]
Decomposition of Permutations¶
Any permutation can be written in terms of the generators of the group.
Let us verify this statement. We consider a random element of the full
symmetric permutation group of 10 elements. We call this group S10.
gap.set('S10', 'SymmetricGroup(10)')
gap.get('S10')
and we see SymmetricGroup( [ 1 .. 10 ] ),
a group of size 10!. We generate a random element of this group:
gap.set('r', 'Random(S10)')
gap.get('r')
and our random element r is ( 1, 3, 7)( 2,10, 6, 5, 4)( 8, 9).
Can we write r in terms of the generators of S10?
Let us see what the generators of S10 are.
gap.get('GeneratorsOfGroup(S10)')
and we see there are only two generators,
as the list shown is [ ( 1, 2, 3, 4, 5, 6, 7, 8, 9,10), (1,2) ].
We assign the list to S10gens and then select from the list
the two generators (lists in GAP start at position 1),
assigning the generators to x and y.
gap.set('S10gens', 'GeneratorsOfGroup(S10)')
gap.set('x', 'S10gens[1]')
gap.set('y', 'S10gens[2]')
Then we define the group generated by x and y as follows;
gap.set('G', 'FreeGroup("x", "y")')
gap.get('G')
nand we see Group( [ x, y ]). We declared G as a FreeGroup
because there are no relations between the generators x and y.
Our problem is now to write r in terms of x and y.
To accomplish this, we define a group homomorphism between G
and S10.
gap.set('hom', \
'GroupHomomorphismByImages( G, S10, GeneratorsOfGroup(G), GeneratorsOfGroup(S10))' )
print gap.get('hom')
The print statement confirms that the operation succeeded.
Then we can ask GAP to compute the representation of r in terms
of the generators of G.
gap.set('p', 'PreImagesRepresentative(hom, r)')
gap.get('p')
and we obtain
y^-1*x^-1*y*x*y*x^-2*y^-1*x^6*(x*y)^4*x^5*(y*x^-1)^2*y*x^2*(y*x^-1)^2*x^-3
as the way r is defined in terms of x and y.
But how can we verify that p is really equal to
( 1, 3, 7)( 2,10, 6, 5, 4)( 8, 9)?
We encountered this problem in symbolic computation before,
how do we compute that two expressions represent the same object?
Consider the following instructions:
xrep = gap.get('x')
print(xrep, 'has type', type(xrep))
and what is printed is
( 1, 2, 3, 4, 5, 6, 7, 8, 9,10) <type 'str'>
confirming that xrep is a string.
To solve our verification problem, we will replace in p
all instances of x and y by their string representations,
using the replace() method on Python strings.
yrep = gap.get('y')
prep = gap.get('p')
rpx = prep.replace('x',xrep)
rpxy = rpx.replace('y',yrep)
Now we have one long complicated string in rpxy.
We can ask GAP to evaluate the expression defined in rpxy.
gap(rpxy)
and what is printed is ( 1, 3, 7)( 2,10, 6, 5, 4)( 8, 9),
the random element r we started with.
This confirms the writing of r as p, an expression
in the generators x and y.
Rubik’s Cube¶
A three dimensional combination cube was invented in 1974 by Ernoe Rubik. As each face rotates independently, the colors of the side mix up. Rubik’s cube is shown in Fig. 94.

Fig. 94 Rubik’s cube.¶
One of the examples of applications of GAP is described at <http://www.gap-system.org/Doc/Examples/rubik.html> by Martin Schoenert. To define the group actions on the cube, we need to number the tiles as shown in Fig. 95.
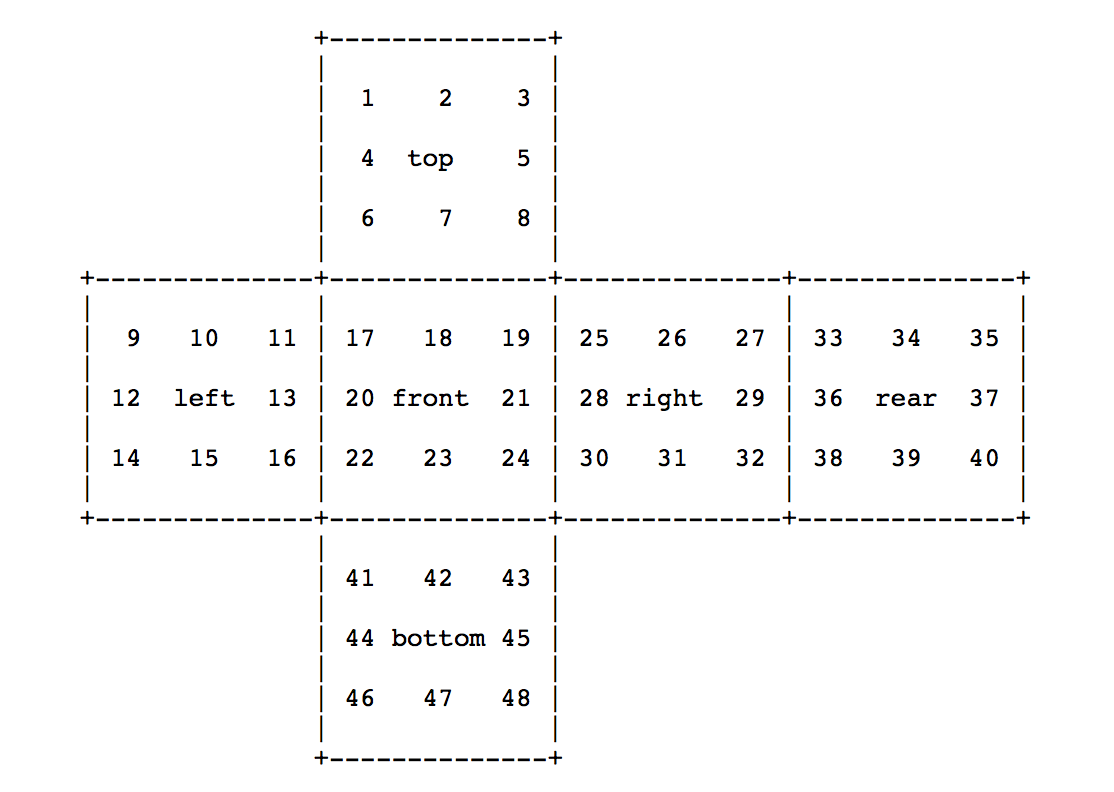
Fig. 95 The numbers on Rubik’s cube to define the group actions.¶
The state of the cube is described by a permutation on 48 numbers.
Turning the front face is described by the permutation
(17,19,24,22)(18,21,23,20)( 6,25,43,16)( 7,28,42,13)( 8,30,41,11)
which consist of 5 cycles, with meaning
(17,19,24,22) : 17 -> 19 -> 24 -> 22 -> 17,
(18,21,23,20) : 18 -> 21 -> 23 -> 23 -> 20,
( 6,25,43,16) : 6 -> 25 -> 43 -> 16 -> 6,
( 7,28,42,13) : 7 -> 28 -> 42 -> 13 -> 7,
( 8,30,41,11) : 8 -> 30 -> 41 -> 11 -> 8.
Turning top, left, right, rear, and bottom are respectively defined by
( 1, 3, 8, 6)( 2, 5, 7, 4)( 9,33,25,17)(10,34,26,18)(11,35,27,19),
( 9,11,16,14)(10,13,15,12)( 1,17,41,40)( 4,20,44,37)( 6,22,46,35),
(25,27,32,30)(26,29,31,28)( 3,38,43,19)( 5,36,45,21)( 8,33,48,24),
(33,35,40,38)(34,37,39,36)( 3, 9,46,32)( 2,12,47,29)( 1,14,48,27), and
(41,43,48,46)(42,45,47,44)(14,22,30,38)(15,23,31,39)(16,24,32,40).
To analyze Rubik’s cube we define a group with six elements. To rotate the front of the cube we apply the front action.
gap.set('front', '(17,19,24,22)(18,21,23,20)( 6,25,43,16)( 7,28,42,13)( 8,30,41,11)')
gap.get('front')
Similarly, we define the top, left, right, rear, and bottom. We then define the group as generated by these six elements.
gap.set('top', '( 1, 3, 8, 6)( 2, 5, 7, 4)( 9,33,25,17)(10,34,26,18)(11,35,27,19)')
gap.set('left', '( 9,11,16,14)(10,13,15,12)( 1,17,41,40)( 4,20,44,37)( 6,22,46,35)')
gap.set('right', '(25,27,32,30)(26,29,31,28)( 3,38,43,19)( 5,36,45,21)( 8,33,48,24)')
gap.set('rear', '(33,35,40,38)(34,37,39,36)( 3, 9,46,32)( 2,12,47,29)( 1,14,48,27)')
gap.set('bottom', '(41,43,48,46)(42,45,47,44)(14,22,30,38)(15,23,31,39)(16,24,32,40)')
gap.set('cube', 'Group( front, top, left, right, rear, bottom)')
gap.get('cube')
We would like to know the size of the group.
size = gap('Size(cube)')
print(size)
print(size.sage().factor())
The size of the group is 43252003274489856000.
Notice that we first have to convert the number to a Sage object
before we can apply factor to see 2^27 * 3^14 * 5^3 * 7^2 * 11.
As in the previous section, we will now decompose a random element r.
The random element represents some arbitrary state of the cube.
The decomposition of r tells how to obtain r from the
six generators of the cube. With this decomposition we can restore
the cube from the state r to its original state.
gap.set('r', 'Random(cube)')
gap.set('G', 'FreeGroup( "front", "top", "left", "right", "rear", "bottom")')
Now we define the group homomorphism:
gap.set('hom', 'GroupHomomorphismByImages( G, cube, GeneratorsOfGroup(G), GeneratorsOfGroup(cube))' )
and then finally, we obtain the decomposition:
gap.set('p', 'PreImagesRepresentative(hom, r)')
gap.get('p')
Assignments¶
The dihedral group of order \(2n\) consists of the isometries of a regular \(n\)-gon: (1) the \(n\) rotations through angles \(2 \pi k/n\) for \(k\) from 0 to \(n-1\); and (2) the \(n\) reflections about lines through the center and either through a vertex or bisecting an edge. Use the GAP command
DihedralGroupto generate the dihedral group of size 10. List all elements of this group.Make an interact to visualize the moves in the Rubik’s cube. There are six sliders, one for turning each side of the cube. After each move of the slider, the current state of the cube is printed as a permutation of 48 numbers.
As a continuation of the previous exercise, instead of printing the state of the cube as one vector of numbers, design a drawing of the six sides of the cube with numbered tiles and different colors for each side.
Study <http://www.gap-system.org/Doc/Examples/rubik.html> to understand how to decompose any element in the group in terms of its generators. Illustrate your understanding with a meaningful computation in a Sage worksheet.
After successfully completing the previous three exercises, augment the interact that allows the user to arbitrarily slide the sides of the cube with a solver. The solver applies GAP to turn the current state of the cube into its solved state.
Deploy the interact of the previous exercise on your personal web page at <http://people.uic.edu>.