Using MPI

We illustrate the collective communication commands to scatter data and gather results. Point-to-point communication happens via a send and a recv (receive) command.

Scatter and Gather

Consider the addition of 100 numbers on a distributed memory 4-processor computer. For simplicity of coding, we sum the first one hundred positive integers and compute

\[S = \sum_{i=1}^{100} i.\]

A parallel algorithm to sum 100 numbers proceeds in four stages:

1. distribute 100 numbers evenly among the 4 processors;

2. Every processor sums 25 numbers;

3. Collect the 4 sums to the manager node; and

4. Add the 4 sums and print the result.

Scattering an array of 100 number over 4 processors and gathering the partial sums at the 4 processors to the root is displayed in Fig. 19.

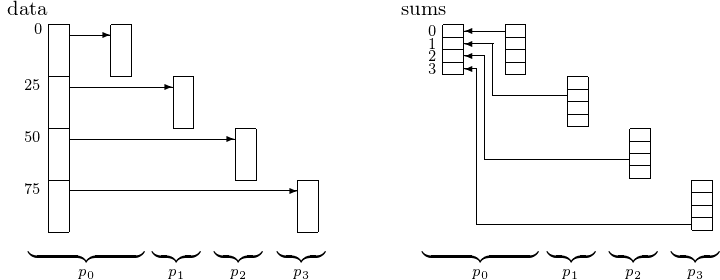
Fig. 19 Scattering data and gathering results.

The scatter and gather are of the collective communication type, as every process in the universe participates in this operation. The MPI commands to scatter and gather are respectively MPI_Scatter and MPI_Gather.

The specifications of the MPI command to scatter data from one member to all members of a group are described in Table 3. The specifications of the MPI command to gather data from all members to one member in a group are listed Table 4.

Table 3 Arguments of the MPI_Scatter command.

MPI_SCATTER(sendbuf,sendcount,sendtype,recvbuf,recvcount,recvtype,root,comm)
sendbuf	address of send buffer
sendcount	number of elements sent to each process
sendtype	data type of send buffer elements
recvbuf	address of receive buffer
recvcount	number of elements in receive buffer
recvtype	data type of receive buffer elements
root	rank of sending process
comm	communicator

Table 4 Arguments of the MPI_Gather command.

MPI_GATHER(sendbuf,sendcount,sendtype,recvbuf,recvcount,recvtype,root,comm)
sendbuf	starting address of send buffer
sendcount	number of elements in send buffer
sendtype	data buffer of send buffer elements
recvbuf	address of receive buffer
recvcount	number of elements for any single receive
recvtype	data type of receive buffer elements
root	rank of receiving process
comm	communicator

The code for parallel summation, in the program parallel_sum.c, illustrates the scatter and the gather.

#include <stdio.h>
#include <stdlib.h>
#include <mpi.h>

#define v 1 /* verbose flag, output if 1, no output if 0 */

int main ( int argc, char *argv[] )
{
   int myid,j,*data,tosum[25],sums[4];

   MPI_Init(&argc,&argv);
   MPI_Comm_rank(MPI_COMM_WORLD,&myid);

   if(myid==0) /* manager allocates and initializes the data */
   {
      data = (int*)calloc(100,sizeof(int));
      for (j=0; j<100; j++) data[j] = j+1;
      if(v>0)
      {
         printf("The data to sum : ");
         for (j=0; j<100; j++) printf(" %d",data[j]); printf("\n");
      }
   }

   MPI_Scatter(data,25,MPI_INT,tosum,25,MPI_INT,0,MPI_COMM_WORLD);

   if(v>0) /* after the scatter, every node has 25 numbers to sum */
   {
      printf("Node %d has numbers to sum :",myid);
      for(j=0; j<25; j++) printf(" %d", tosum[j]);
      printf("\n");
   }
   sums[myid] = 0;
   for(j=0; j<25; j++) sums[myid] += tosum[j];
   if(v>0) printf("Node %d computes the sum %d\n",myid,sums[myid]);

   MPI_Gather(&sums[myid],1,MPI_INT,sums,1,MPI_INT,0,MPI_COMM_WORLD);

   if(myid==0) /* after the gather, sums contains the four sums */
   {
      printf("The four sums : ");
      printf("%d",sums[0]);
      for(j=1; j<4; j++) printf(" + %d", sums[j]);
      for(j=1; j<4; j++) sums[0] += sums[j];
      printf(" = %d, which should be 5050.\n",sums[0]);
   }
   MPI_Finalize();
   return 0;
}

Send and Recv

To illustrate point-to-point communication, we consider the problem of squaring numbers in an array. An example of an input sequence is \(2, 4, 8, 16, \ldots\) with corresponding output sequence \(4, 16, 64, 256, \ldots\). Instead of squaring, we could apply a difficult function \(y = f(x)\) to an array of values for \(x\). A session with the parallel code with 4 processes runs as

$ mpirun -np 4 /tmp/parallel_square
The data to square :  2 4 8 16
Node 1 will square 4
Node 2 will square 8
Node 3 will square 16
The squared numbers :  4 16 64 256
$

Applying a parallel squaring algorithm to square \(p\) numbers runs in three stages:

1. The manager sends \(p-1\) numbers \(x_1, x_2, \ldots,x_{p-1}\) to workers. Every worker receives: the \(i\)-th worker receives \(x_i\) in \(f\). The manager copies \(x_0\) to \(f\): \(f = x_0\).

2. Every node (manager and all workers) squares \(f\).

3. Every worker sends \(f\) to the manager. The manager receives \(x_i\) from \(i\)-th worker, \(i=1,2,\ldots,p-1\). The manager copies \(f\) to \(x_0\): \(x_0 = f\), and prints.

To perform point-to-point communication with MPI are MPI_Send and MPI_Recv. The syntax for the blocking send operation is in Table 5. Table 6 explains the blocking receive operation.

Table 5 The MPI_SEND command.

MPI_SEND(buf,count,datatype,dest,tag,comm)
buf	initial address of the send buffer
count	number of elements in send buffer
datatype	data type of each send buffer element
dest	rank of destination
tag	message tag
comm	communication

Table 6 The MPI_RECV command.

MPI_RECV(buf,count,datatype,source,tag,comm,status)
buf	initial address of the receive buffer
count	number of elements in receive buffer
datatype	data type of each receive buffer element
source	rank of source
tag	message tag
comm	communication
status	status object

Code for a parallel square is below. Every MPI_Send is matched by a MPI_Recv. Observe that there are two loops in the code. One loop is explicitly executed by the root. The other, implicit loop, is executed by the mpiexec -n p command.

#include <stdio.h>
#include <stdlib.h>
#include <mpi.h>

#define v 1 /* verbose flag, output if 1, no output if 0 */
#define tag 100 /* tag for sending a number */

int main ( int argc, char *argv[] )
{
   int p,myid,i,f,*x;
   MPI_Status status;
   MPI_Init(&argc,&argv);
   MPI_Comm_size(MPI_COMM_WORLD,&p);
   MPI_Comm_rank(MPI_COMM_WORLD,&myid);
   if(myid == 0) /* the manager allocates and initializes x */
   {
      x = (int*)calloc(p,sizeof(int));
      x[0] = 2;
      for (i=1; i<p; i++) x[i] = 2*x[i-1];
      if(v>0)
      {
         printf("The data to square : ");
         for (i=0; i<p; i++) printf(" %d",x[i]); printf("\n");
      }
   }
   if(myid == 0) /* the manager copies x[0] to f */
   {             /* and sends the i-th element to the i-th processor */
      f = x[0];
      for(i=1; i<p; i++) MPI_Send(&x[i],1,MPI_INT,i,tag,MPI_COMM_WORLD);
   }
   else /* every worker receives its f from root */
   {
      MPI_Recv(&f,1,MPI_INT,0,tag,MPI_COMM_WORLD,&status);
      if(v>0) printf("Node %d will square %d\n",myid,f);
   }
   f *= f;       /* every node does the squaring */
   if(myid == 0) /* the manager receives f in x[i] from processor i */
      for(i=1; i<p; i++)
         MPI_Recv(&x[i],1,MPI_INT,i,tag,MPI_COMM_WORLD,&status);
   else     /* every worker sends f to the manager */
      MPI_Send(&f,1,MPI_INT,0,tag,MPI_COMM_WORLD);
   if(myid == 0) /* the manager prints results */
   {
      x[0] = f;
      printf("The squared numbers : ");
      for(i=0; i<p; i++) printf(" %d",x[i]); printf("\n");
   }
   MPI_Finalize();
   return 0;
}

Reducing the Communication Cost

The wall time refers to the time elapsed on the clock that hangs on the wall, that is: the real time, which measures everything, not just the time the processors were busy. To measure the communication cost, we run our parallel program without any computations. MPI_Wtime() returns a double containing the elapsed time in seconds since some arbitrary time in the past. An example of its use is below.

double startwtime,endwtime,totalwtime;
startwtime = MPI_Wtime();
/* code to be timed */
endwtime = MPI_Wtime();
totalwtime = endwtime - startwtime;

A lot of time in a parallel program can be spent on communication. Broadcasting over 8 processors sequentially takes 8 stages. In a fan out broadcast, the 8 stages are reduced to 3. Fig. 20 illustrates the sequential and fan out broadcast.

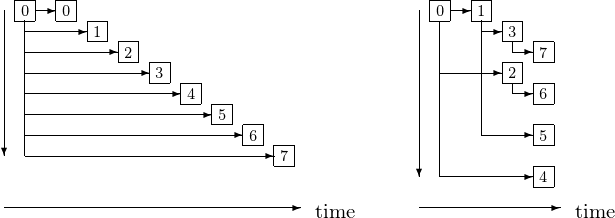
Fig. 20 Sequential (left) versus fan out (right) broadcast.

The story of Fig. 20 can be told as follows. Consider the distribution of a pile of 8 pages among 8 people. We can do this in three stages:

1. Person 0 splits the pile keeps 4 pages, hands 4 pages to person 1.

2. Person 0 splits the pile keeps 2 pages, hands 2 pages to person 2.

   Person 1 splits the pile keeps 2 pages, hands 2 pages to person 3.

3. Person 0 splits the pile keeps 1 page, hands 1 pages to person 4.

   Person 1 splits the pile keeps 1 page, hands 1 pages to person 5.

   Person 2 splits the pile keeps 1 page, hands 1 pages to person 6.

   Person 3 splits the pile keeps 1 page, hands 1 pages to person 7.

Already from this simple example, we observe the pattern needed to formalize the algorithm. At stage \(k\), processor \(i\) communicates with the processor with identification number \(i + 2^k\).

The algorithm for fan out broadcast has a short description, shown below.

Algorithm: at step k, 2**(k-1) processors have data, and execute:

for j from 0 to 2**(k-1) do
    processor j sends to processor j + 2**(k-1);
    processor j+2**(k-1) receives from processor j.

The cost to broadcast of one item is \(O(p)\) for a sequential broadcast, is \(O(\log_2(p))\) for a fan out broadcast. The cost to scatter \(n\) items is \(O(p \times n/p)\) for a sequential broadcast, is \(O(\log_2(p) \times n/p)\) for a fan out broadcast.

Point-to-Point Communication with MPI for Python

In MPI for Python we call the methods send and recv for point-to-point communication. Process 0 sends DATA to process 1:

MPI.COMM_WORLD.send(DATA, dest=1, tag=2)

Every send must have a matching recv. For the script to continue, process 1 must do

DATA = MPI.COMM_WORLD.recv(source=0, tag=2)

mpi4py uses pickle on Python objects. The user can declare the MPI types explicitly.

What appears on screen running the Python script is below.

$ mpiexec -n 2 python mpi4py_point2point.py
0 sends {'a': 7, 'b': 3.14} to 1
1 received {'a': 7, 'b': 3.14} from 0

The script mpi4pi_point2point.py is below.

from mpi4py import MPI

COMM = MPI.COMM_WORLD
RANK = COMM.Get_rank()

if(RANK == 0):
    DATA = {'a': 7, 'b': 3.14}
    COMM.send(DATA, dest=1, tag=11)
    print RANK, 'sends', DATA, 'to 1'
elif(RANK == 1):
    DATA = COMM.recv(source=0, tag=11)
    print RANK, 'received', DATA, 'from 0'

With mpi4py we can either rely on Python’s dynamic typing or declare types explicitly when processing numpy arrays. To sum an array of numbers, we distribute the numbers among the processes that compute the sum of a slice. The sums of the slices are sent to process 0 which computes the total sum. The code for the script is mpi4py_parallel_sum.py and what appears on screen when the script runs is below.

$ mpiexec -n 10 python mpi4py_parallel_sum.py
0 has data [0 1 2 3 4 5 6 7 8 9] sum = 45
2 has data [20 21 22 23 24 25 26 27 28 29] sum = 245
3 has data [30 31 32 33 34 35 36 37 38 39] sum = 345
4 has data [40 41 42 43 44 45 46 47 48 49] sum = 445
5 has data [50 51 52 53 54 55 56 57 58 59] sum = 545
1 has data [10 11 12 13 14 15 16 17 18 19] sum = 145
8 has data [80 81 82 83 84 85 86 87 88 89] sum = 845
9 has data [90 91 92 93 94 95 96 97 98 99] sum = 945
7 has data [70 71 72 73 74 75 76 77 78 79] sum = 745
6 has data [60 61 62 63 64 65 66 67 68 69] sum = 645
total sum = 4950

The code for the script mpi4py_parallel_sum.py follows.

from mpi4py import MPI
import numpy as np

COMM = MPI.COMM_WORLD
RANK = COMM.Get_rank()
SIZE = COMM.Get_size()
N = 10

if(RANK == 0):
    DATA = np.arange(N*SIZE, dtype='i')
    for i in range(1, SIZE):
        SLICE = DATA[i*N:(i+1)*N]
        COMM.Send([SLICE, MPI.INT], dest=i)
    MYDATA = DATA[0:N]
else:
    MYDATA = np.empty(N, dtype='i')
    COMM.Recv([MYDATA, MPI.INT], source=0)

S = sum(MYDATA)
print RANK, 'has data', MYDATA, 'sum =', S

SUMS = np.zeros(SIZE, dtype='i')
if(RANK > 0):
    COMM.send(S, dest=0)
else:
    SUMS[0] = S
    for i in range(1, SIZE):
        SUMS[i] = COMM.recv(source=i)
    print 'total sum =', sum(SUMS)

Recall that Python is case sensitive and the distinction between Send and send, and between Recv and recv is important. In particular, COMM.send and COMM.recv have no type declarations, whereas COMM.Send and COMM.Recv have type declarations.

Point-to-Point Communication with the MPI wrappers in Julia

The code below illustrates the sending and receiving of a dictionary between two nodes, using the MPI wrappers for Julia.

using MPI
MPI.Init()

comm = MPI.COMM_WORLD
myid = MPI.Comm_rank(comm)

if myid == 0
    data = Dict('a' => 7, 'b' => 3.14)
    println("$myid sends $data to 1")
    MPI.send(data, comm; dest=1, tag=11)
elseif myid == 1
    data = MPI.recv(comm; source=0, tag=11)
    println("$myid received $data from 0")
end

Running in a Terminal Windows, at the command prompt:

$ mpiexecjl -n 2 julia mpi_point2point.jl
0 sends Dict{Char, Real}('a' => 7, 'b' => 3.14) to 1
1 received Dict{Char, Real}('a' => 7, 'b' => 3.14) from 0

Bibliography

1. S. Byrne, L.C. Wilcox, and V. Churavy: MPI.jl: Julia bindings for the Message Passing Interface. In JuliaCon Proceedings, 1(1), 68, 2021.

2. L. Dalcin, R. Paz, and M. Storti. MPI for Python. Journal of Parallel and Distributed Computing, 65:1108–1115, 2005.

3. M. Snir, S. Otto, S. Huss-Lederman, D. Walker, and J. Dongarra. MPI - The Complete Reference Volume 1, The MPI Core. Massachusetts Institute of Technology, second edition, 1998.

Exercises

1. Adjust the parallel summation to work for \(p\) processors where the dimension \(n\) of the array is a multiple of \(p\).

2. Use C or Julia to rewrite the program to sum 100 numbers using MPI_Send and MPI_Recv instead of MPI_Scatter and MPI_Gather. In Python, use the collective instead of point-to-point communication.

3. Use C, Python, or Julia to rewrite the program to square \(p\) numbers using MPI_Scatter and MPI_Gather.

4. Show that a hypercube network topology has enough direct connections between processors for a fan out broadcast.