Introduction to Tensor Cores

Training deep neural networks is computationally expensive. Tensor cores accelerate convolutions and matrix operations, for use to accelerate high performance computing, data center, and machine learning applications.

While targeted to General Matrix Multiply (GEMM), convolution operations can be reduced to GEMM. The tensor core peak performance in double precision increased from 19.5 on Ampere A100 to 134 TFLOPS on Hopper H100.

High Throughput Computing

The Volta V100 gives a 12-fold increase in throughput, compared to the Pascal P100.

definition of throughput

Throughput measures how much information a system can process in a given amount of time.

High Performance Computing (HPC) measures FLOPS. High Throughput Computing (HTC) measures the number of jobs that can be completed over a long period. While related, HPC is concerned with speed, HTC is also concerned with robustness and reliability.

Volta, Ampere, Hopper Architectures

Each Streaming Multiprocessor (SM) on Volta, shown in Fig. 116 has 8 Tensor cores. With 80 SMs, there are 640 tensor cores in total, yielding 125 tensor TFLOPS of mixed precision.

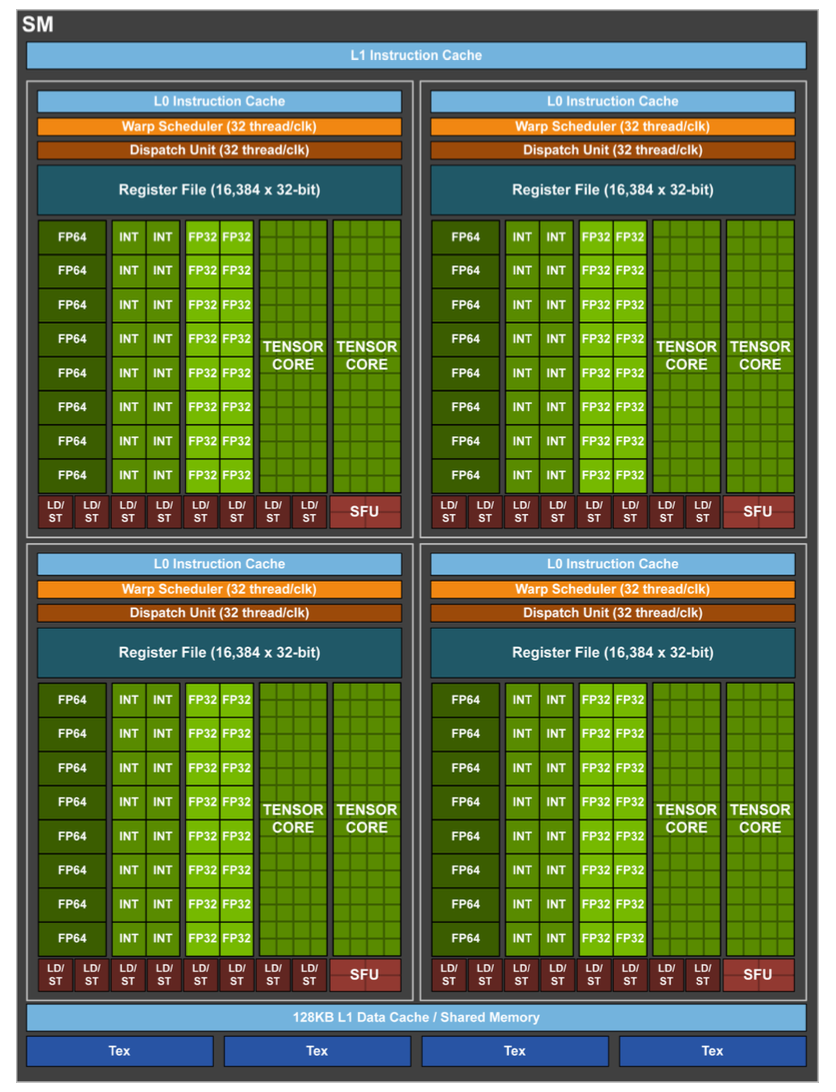
Fig. 116 The Volta Streaming Multiprocessor, picture from the NVIDIA Volta Architecture white paper.

The comparison between Volta V100 and Ampere A100 is illustrated in Fig. 117 and Fig. 118 compare the Ampere A100 with the Hopper H100.

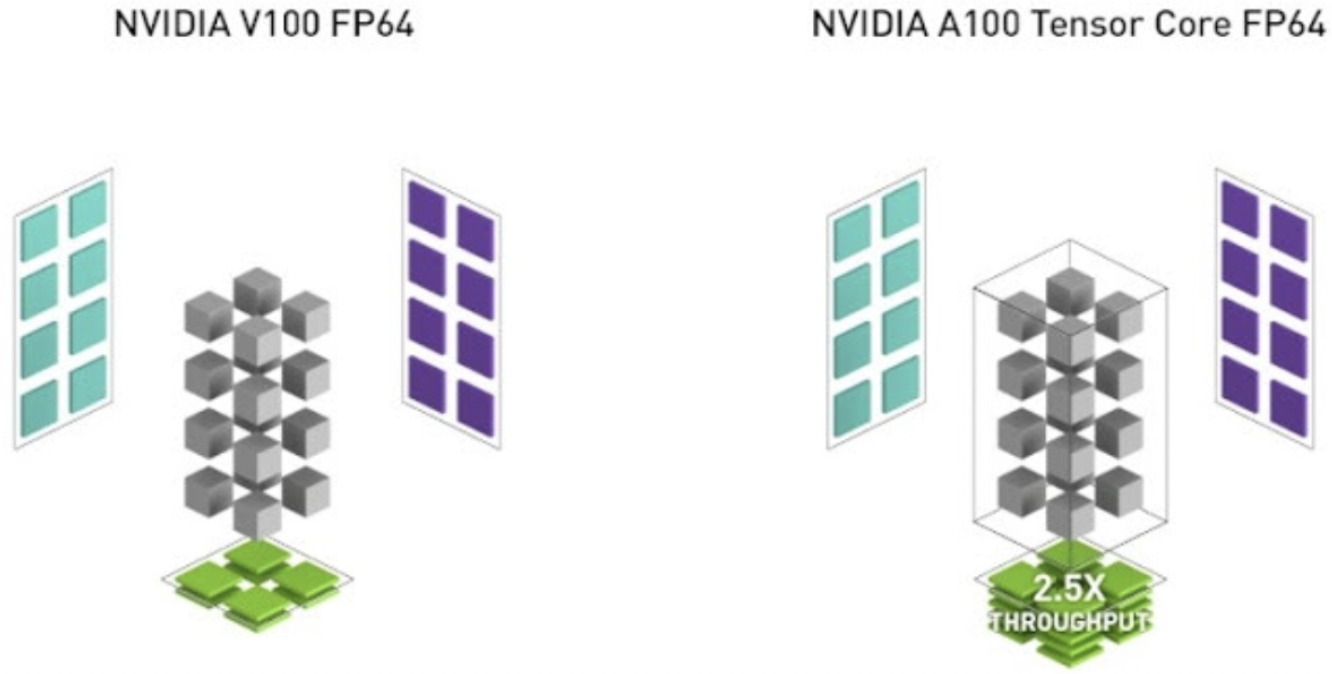
Fig. 117 The V100 versus the A100, picture from the NVIDIA Ampere Architecture white paper.

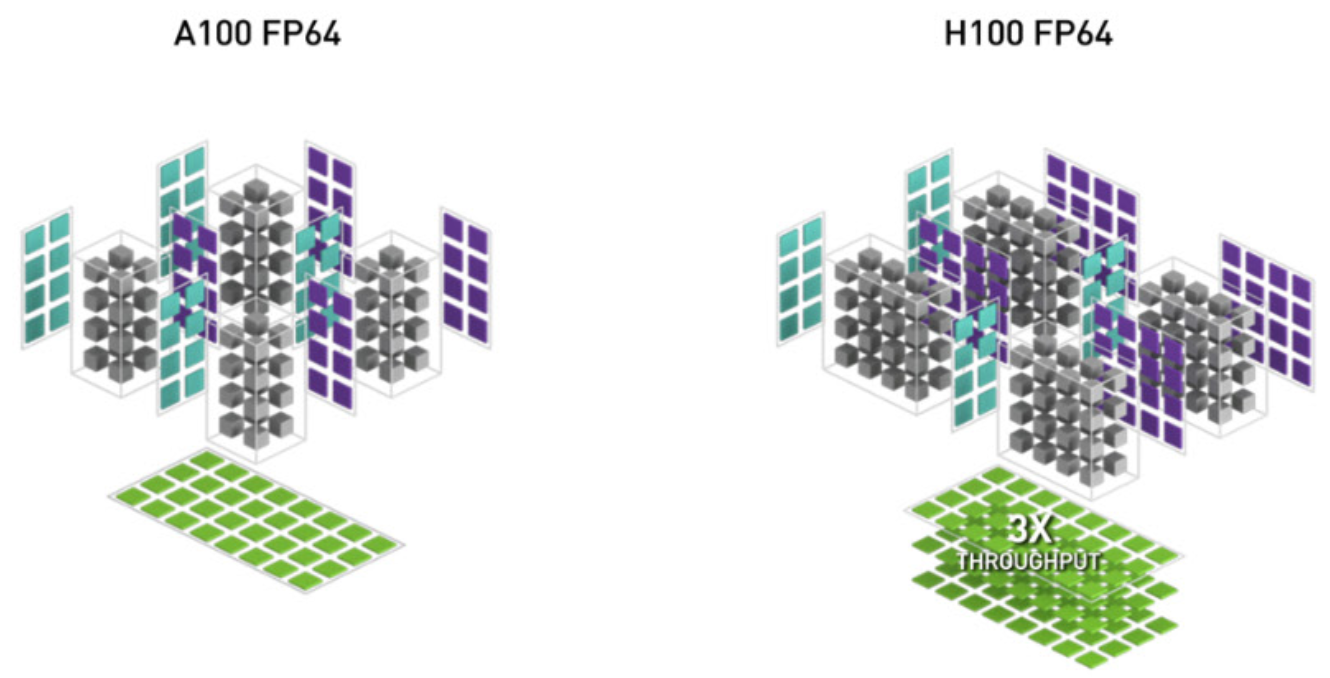
Fig. 118 The A100 versus the H100, picture from the NVIDIA Hopper Architecture white paper.

Tensor cores execute mixed precision matrix operations, illustrated in Fig. 119.

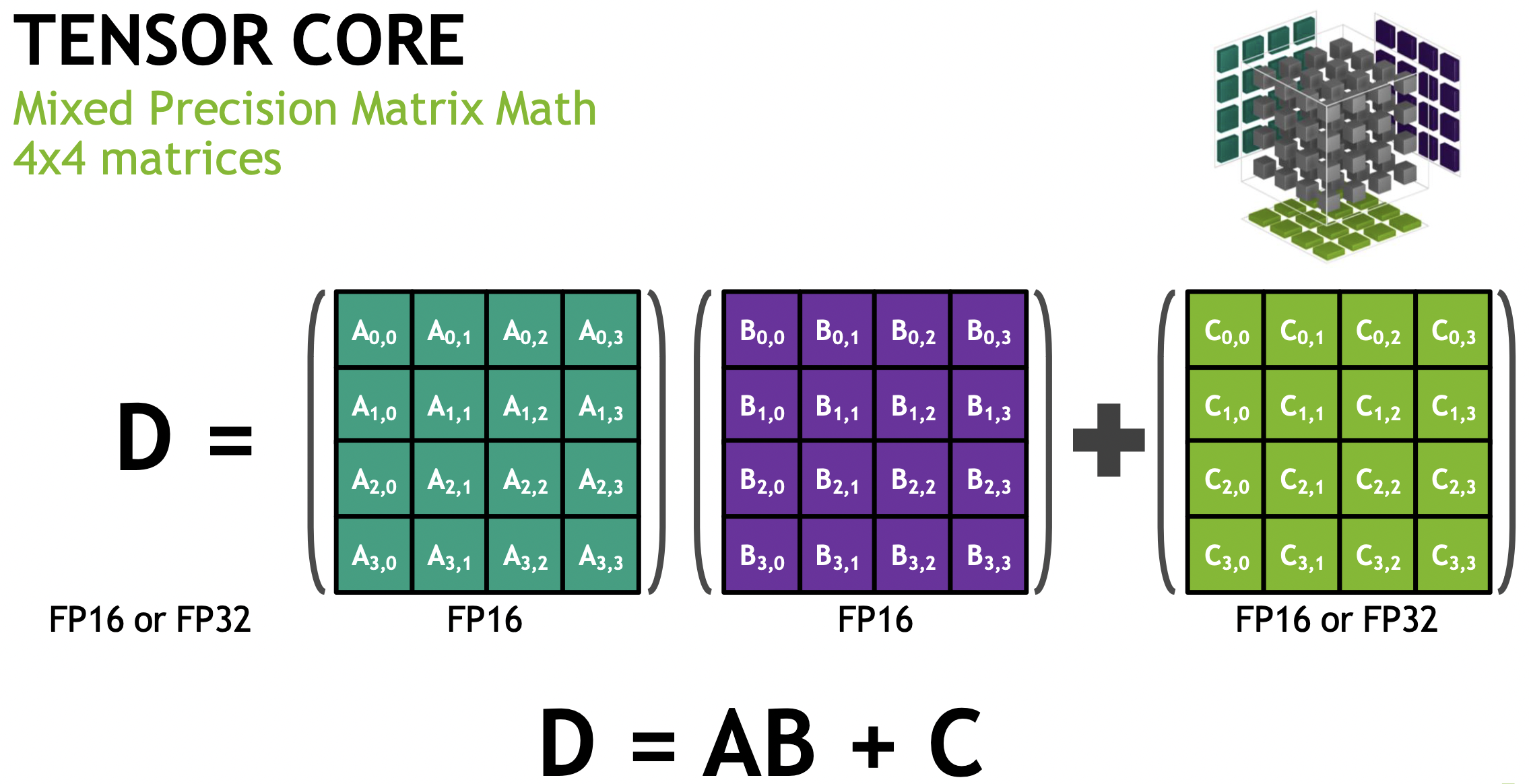
Fig. 119 Mixed Precision Matrix Math, picture taken from presentation at SC 2019 by Vishal Mehta on getting started with tensor cores in HPC.

Reading Release 12.1 of the CUDA C++ Programming Guide, section 10.2.4, 28 February 2023, about Warp Matrix Functions:

• For compute capability 7.0 or higher.

• Double precision is supported for compute capability at least 8.0.

• All threads in a warp must execute the same code. Code execution is likely to hang otherwise.

• A fragment is a templated type with template parameters describing which matrix the fragment holds (\(A\), \(B\) or accumulator), the shape of the overall WMMA operation, the data type and, for \(A\) and \(B\) matrices, whether the data is row or column major.

On a Volta computer, in the folder /usr/local/cuda/samples/0_Simple/cudaTensorCoreGemm the output of running an example is below:

$ ./cudaTensorCoreGemm
Initializing...
GPU Device 0: "Quadro GV100" with compute capability 7.0

M: 4096 (16 x 256)
N: 4096 (16 x 256)
K: 4096 (16 x 256)
Preparing data for GPU...
Required shared memory size: 64 Kb
Computing... using high performance kernel compute_gemm
Time: 2.768896 ms
TFLOPS: 49.64
$

On ampere, in the folder cudaTensorCoreGemm of /usr/local/cuda/samples/Samples/3_CUDA_Features the same example is found and below is the output on a a run on the A100.

$ ./cudaTensorCoreGemm
Initializing...
GPU Device 0: "Ampere" with compute capability 8.0

M: 4096 (16 x 256)
N: 4096 (16 x 256)
K: 4096 (16 x 256)
Preparing data for GPU...
Required shared memory size: 64 Kb
Computing... using high performance kernel compute_gemm
Time: 1.756160 ms
TFLOPS: 78.26
$

Observe the increase in performance of the A100 over the V100. A short explanation of what was computed follows. The Warp Matrix Multipy and Accumulate (WMMA) computes

\[D = \alpha A B + \beta C\]

where

• matrix \(A\) is M-by-K row major,

• matrix \(B\) is K-by-N column major, and

• matrices \(C\) and \(D\) are M-by-N.

Each Cooperative Thread Array (CTA) consists of 8 warps and computes one 128-by-128 tile, using shared memory for the matrix \(C\).

Simple Matrix Multiplication

The explanations in this section are based on a 2017 NVIDIA Technical Blog, by Jeremy Appleyard and Scott Yokim, available from <https://developer.nvidia.com/blog> on Programming Tensor Cores in CUDA 9.

The demonstration code is available on github via <https://github.com/NVIDIA-developer-blog/code-samples> posted with a Makefile. It show the use of the WMMA (Warp Matrix Multiply Accumulate) API to perform a matrix multiplication.

• For performance, use the cudaTensorCoreGemm in the CUDA Toolkit.

• For highest performance, use cuBLAS.

There are four steps in the demonstration code:

1. Use headers and namespaces.

2. Declarations and initialization:

   A simple warp is responsible for a single 16-by-16 section of the output matrix. Tiling happens with a 2D grid:

   int warpM = (blockIdx.x*blockDim.x+threadIdx.x)/ warpSize;
   int warpN = (blockIdx.y*blockDim.y+threadIdx.y);
   

3. The inner loop performs the matrix multiplication.

4. Finishing up: store the accumulated data to memory.

A fragment is a templated type with parameters as follows:

1. which matrix the fragment holds, A, B, or accumulator;

2. the shape of the overall WMMA operation;

3. the data type;

4. for A and B matrices, whether the data is row or column major.

The parameters are specified at the declaration of the fragment. Accumulator fragments are filled with zeros at initialization. Declaration of the fragments is done in the code below:

wmma::fragment<wmma::matrix_a, WMMA_M, WMMA_N, WMMA_K, half, wmma::col_major> a_frag;
wmma::fragment<wmma::matrix_b, WMMA_M, WMMA_N, WMMA_K, half, wmma::col_major> b_frag;
wmma::fragment<wmma::accumulator, WMMA_M, WMMA_N, WMMA_K, float> acc_frag;
wmma::fragment<wmma::accumulator, WMMA_M, WMMA_N, WMMA_K, float> c_frag;

Initialization of the accumulator fragment happens as follows:

wmma::fill_fragment(acc_frag, 0.0f);

One tile of the output matrix is computed by one warp.

• The loop runs over the rows of A and columns of B, to produce an m-by-n output tile.

• Data is loaded from global memory into a fragment.

• If a tile is discontinous in memory, the stride must be provided to the load function.

• The Matrix Multiply Accumulate (MMA) accumulates in place, so both first and last arguments are the accumulator fragment previously initialized to zero.

The headers and declarations are in the code blocks below:

#include <mma.h>
using namespace nvcuda;

// Must be multiples of 16 for wmma code to work
#define MATRIX_M 16384
#define MATRIX_N 16384
#define MATRIX_K 16384

// The only dimensions currently supported by WMMA
const int WMMA_M = 16;
const int WMMA_N = 16;
const int WMMA_K = 16;

Below is the listing of the start of the kernel:

// Performs an MxNxK GEMM (C=alpha*A*B + beta*C) assuming:
//  1) Matrices are packed in memory.
//  2) M, N and K are multiples of 16.
//  3) Neither A nor B are transposed.
__global__ void wmma_example
  ( half *a, half *b, float *c,
    int M, int N, int K, float alpha, float beta)
{
    // Leading dimensions.
    int lda = M;
    int ldb = K;
    int ldc = M;

That there is only a single loop is because of the two dimensional organization of the threads. Code for the loop is below:

for (int i = 0; i < K; i += WMMA_K)
{
   int aRow = warpM * WMMA_M;
   int aCol = i;

   int bRow = i;
   int bCol = warpN * WMMA_N;

   // Bounds checking
   if (aRow < M && aCol < K && bRow < K && bCol < N)
   {
      // Load the inputs
      wmma::load_matrix_sync(a_frag, a+aRow+aCol*lda, lda);
      wmma::load_matrix_sync(b_frag, b+bRow+bCol*ldb, ldb);

      // Perform the matrix multiplication
      wmma::mma_sync(acc_frag, a_frag, b_frag, acc_frag);
   }
}

Observe the computation of the indices for the arguments of load_matrix_sync.

The code below loads the current value of c, scales it by beta and adds this to our result scaled by alpha.

int cRow = warpM * WMMA_M;
int cCol = warpN * WMMA_N;

if (cRow < M && cCol < N)
{
   wmma::load_matrix_sync(c_frag, c + cRow + cCol * ldc,
                          ldc, wmma::mem_col_major);

#pragma unroll
   for(int i=0; i < c_frag.num_elements; i++)
   {
      c_frag.x[i] = alpha * acc_frag.x[i] + beta * c_frag.x[i];
   }
   // Store the output
   wmma::store_matrix_sync(c + cRow + cCol * ldc, c_frag,
                           ldc, wmma::mem_col_major);
}

The output of runs on volta and ampere are listed next:

$ ./TCGemm

M = 16384, N = 16384, K = 16384.  alpha = 2.000000, beta = 2.000000

Running with wmma...
Running with cuBLAS...

Checking results...
Results verified: cublas and WMMA agree.

On the Volta V100, we obtain:

wmma took 631.051270ms
cublas took 99.577888ms

On the Ampere A100:

wmma took 501.762054ms
cublas took 38.711296ms

While A100 is (at least) twice as fast as V100, the performance of the simple matrix multiplication is disappointing, which emphasizes the point that running simple code on faster computer is often pointless.

Bibliography

1. NVIDIA. CUDA C++ Programming Guide.

2. Da Yan, Wei Wang, Xiaowen Chu: Demystifying Tensor Cores to Optimize Half-Precision Matrix Multiply. In the Proceedings of the 2020 IEEE International Parallel and Distributed Processing Symposium (IPDPS), pages 634–643.

3. Thomas Faingnaert, Tim Besard, and Bjorn De Sutter: Flexible Performant GEMM Kernels on GPUs. IEEE Transactions on Parallel and Distributed Systems 33:(9): 2230–2248, 2022.

4. Massimiliano Fasi, Nicholas J. Higham, Florent Lopez, Theo Mary, and Mantas Mikaitis: Matrix Multiplication in Multiword Arithmetic: Error Analysis and Application to GPU Tensor Cores. SIAM Journal on Scientific Computing 45(1): C1–C19, 2023.

Exercises

1. Let \({\bf x} = (x_0, x_1, x_2, x_3, x_4)\) and \({\bf y} = (y_0, y_1, y_2, y_3, y_4)\) be two vectors and consider its convolution \(x_0 y_4 + x_1 y_3 + x_2 y_2 + x_3 y_1 + x_4 y_0\).

   Demonstrate how to rewrite convolutions as matrix products.

2. Install the Julia package GemmKernels.jl.

   Read the paper by Faingnaert et al. and run an example of matrix multiplication with the package.