The Database of Applications

The polynomial systems in scientific and engineering models are a continuing source of open problems. Systems that come from academic questions are often conjectures providing computational evidence in a developing theory. In various engineering disciplines polynomial systems represent a modeling problem, e.g.: a mechanical device. The origin of a polynomial system matters when the original problem formulation does not admit well-conditioned solutions. As a general method to deal with badly scaled systems to compute equilibria of chemical reaction systems, coefficient and equation scaling was developed in [69], see also [71, Chapter 5] and [124].

The collection of test systems is organized as a database and available via the author's web pages, A good test example reveals properties of the solution method and has a meaningful application. Besides the algebraic formulation it contains the fields: title (meaningful description), references (problem source), root counts (Bézout bounds and mixed volume), and solution list.

Instead of producing a huge list with an overview, we pick some important case studies.

katsura-n

(magnetism problem [47]) The number of solutions equals the total degree D = 2ⁿ, so the homotopy based on D is optimal to solve this problem. Because the constant term is missing in all except one equation, the system is an interesting test problem for affine polyhedral methods.

camera1s

(computer vision [28]) The system models the displacement of a camera between two positions in a static environment [23]. The multi-homogeneous homotopy is optimal for this problem, requiring 20 solution paths to trace instead of D = 64.

gamentwo

(totally mixed Nash equilibria for n players with two strategies [67,68]) This is another instance where multi-homogeneous homotopies are optimal. The number of solutions grows like n! e^-1 as $n \rightarrow \infty$. The largest system that is currently completely solvable is for n = 8 requiring 14,833 paths to trace. Situations exist for which all solutions are meaningful.

cassou

(real algebraic geometry) This system illustrates the success story of polyhedral homotopies: the total degree equals 1,344, best known Bézout bound is 312 (see [63]), whereas the mixed volume gives 24. Still eight paths are diverging to infinity and polyhedral end games [43] are needed to separate those diverging paths from the from the other finite ill-conditioned roots.

cyclic-n

(Fourier transforms [8,9]) For n=7, polyhedral homotopies are optimal, with all 924 paths leading to finite solutions. For 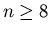$n \geq 8$, the mixed volume overestimates the number of roots and there are components of solutions. In [94] the degrees of the components were computed for n=8,9. There are 34940 cyclic 10-roots, generated by 1747 solutions.

pole28sys

(pole placement problem [12]) This system illustrates the efficiency of SAGBI homotopies for verifying a conjecture in real algebraic geometry [98]. With the input planes chosen to osculate a rational normal curve, an instance with all 1,430 solutions real and isolated was solved in [114]. The problem is relevant to control theory [90].

stewgou40

(mechanism design [18]) Whether the Stewart-Gough parallel platform in robotics could have all its 40 solutions real was a notorious open problem, until recently, as it was solved by numerical continuation methods [18]. The problem formulation in [18] is highly deficient: the mixed volume equals 1,536 whereas only 40 solution paths will converge.

We emphasize that we have optimal homotopies for three classes of polynomial systems, but not for all possible structures. Although one can solve a modelling problem by a black-box polynomial-system solver, knowing the origin of the problem leads in most cases to more favorable algebraic formulations that help the resolution of a polynomial system. To produce really meaningful solutions one often has to be close to the source of the problems and be able to interact with the people who formulate the polynomial systems.

In closing this section we list some notable usages of PHC. Charles Wampler [121] used a preliminary version of PHC to count the roots of various systems in mechanical design. Root counts for linear subspace intersections in the Schubert calculus were computed by Frank Sottile, see [98] for various tables. A third example comes from computer graphics. To show that the 12 lines tangent to four given spheres can all be real, Thorsten Theobald used PHC, choosing appropriate parameters in the algebraic formulation set up by Cassiano Durand.