MthT 491 Mathematics of the Chipboard
MthT 491 Mathematics of the Chipboard
Jeff E. Lewis








This note will follow one of the standard constructions1 of the negative integers and its relation to the Chip Board representation and model for integers.
We shall assume that the natural numbers and 0 - the nonnegative integers - N0 = {0, 1, 2, 3,…} are available and the binary operations of addition, +, and multiplication, · are defined so that
Properties of Addition
P1
For all a, b, c, in N0,
a + (b + c) = (a + b) + c
P2
There is a number 0 in N0 such that for all a,
a + 0 = 0 + a = a.
P3
(Not Yet!) [Additive Inverse]
P4
For all a, b,
a + b = b + a.
P5
For all a, b, c,
a ·(b ·c) = (a ·b) ·c
P6
[Multiplicative Unit] There is a number 1 ≠ 0 such that for all a,
a ·1 = 1 ·a = a.
P7
(Not Yet!) [Multiplicative Inverse]
P8
For all a, b,
a ·b = b ·a.


Property of · with +
P9
(Distributive) For all a, b, c,
a ·(b + c) = (a ·b) + (a·c) = a ·b + a·c.
We have intentionally omitted property (P3) - the additive inverse - which holds for the set of all integers, but which does not hold for the set of nonnegative integers:
P3
Not Yet! For all a, there is a number −a such that
a + (−a) = (−a) + a = 0.
For now, we also omit any mention of a multiplicative inverse :
P7
Not Yet! For all a ≠ 0, there is a number a−1 such that
a ·(a−1) = (a−1) ·a = 1.
The aim is to give a formal construction which will enlarge the set of nonnegative integers to include the negative integers . We will do this by making a formal sense of a − b for any a ≥ 0, b ≥ 0.
Think of a − b as an ordered pair (a,b). There are many different ways (ordered pairs) which give the same result a −b: For any c ≥ 0,
a − b
= (a + c ) − (b + c).
We want to identify (treat as the same) the pair (a,b) with all the pairs (a +c, b + c).
Motivated by the desired behavior of a − b,
a − b = a′− b′
iff
a + b′ = a′+ b,
we define an equivalence relation on ordered pairs (a,b).

Chip Board. Think of the pair (a,b) as a Board with a black chips and b red chips. Adding c black chips and c red chips gives a Board with the same value.

Definition. Consider the collection of all ordered pairs (a,b), a, b ∈ N0. We say that
(a,b)
≅ (a′,b′)
iff a + b′
= a′+ b.
Read (a,b) ≅ (a′,b′) as "The pair (a,b) is equivalent to the pair (a′,b′)."
Note that, for any c ∈  N0,
(a,b) ≅ (a+ c,b + c).
We denote the equivalence class of (a,b) as [a,b].

Chip Board. For any c ≥ 0, the board with a black chips and b red chips is considered the same (has the same value) as the board with a + c black chips and b + c red chips. Moreover, we can go between two equally valued boards by adjoining or taking away pairs of red and black chips.
We can also think of the number a, a ≥ 0, as corresponding to the Board with a black chips and 0 red chips:
a
↔ (a,0)
or a
↔ [a,0].

Chip Board. The Chip Board with 0 black and b red corresponds to the pair (0,b) and also to (c,b +c); thus 0 black and b red corresponds to the equivalence class [0,b].
We must verify that ≅ , is an equivalence relation, i.e., the relation ≅ is
•
reflexive : (a,b) ≅ (a,b),
•
symmetric : if (a,b) ≅ (a,b), then (a′,b′) ≅ (a,b),
•
transitive : if (a,b) ≅ (a′,b′), and (a′,b′) ≅ (a′′,b′′) then (a,b) ≅ (a′′,b′′).

Chip Board. Call an equivalence class the value of any representative board.
•
reflexive : Every Board has the same value as its own value.
•
symmetric : if Board X has the same value as Board Y, then Board Y has the value of Board X.
•
transitive : if Board X has the same value as Board Y, and Board Y has the same value as Board Z, then Board X has the same value as Board Z.
We denote the equivalence class of (a,b) as [a,b].
Next we define an addition and multiplication on equivalence classes, pushing toward making [a,b] a pseudonym for a − b.
For the time being we shall indicate addition by ⊕ and multiplication by ⊗.


Addition
Indicate addition of equivalence classes by ⊕.
If a ≥ b ≥ 0, c ≥ d ≥ 0,
(a − b) +(c −d)
= (a + c)−(b + d).
Motivated by the desire to extend this property, for all a, b, c, d ∈ N0, define

[a,b] ⊕[c,d]
= [a+ c,b +d].

Chip Board. Starting with a black and b red, put down c black and d red.
Note that
•
A Chip Board corresponding to (a,b) can be obtained by putting down a black chips and then putting down b red chips.
•
[a,b] = [a,0] ⊕[0,b].
•
Any Chip Board with value 0 has an equal number of black and red chips - c black chips and c red chips. We call such a board the Null Board ↔[0,0] = [c,c].
•
The Null Board (0,0) serves as a Zero for addition ⊕,
[a,b] ⊕[0,0]
= [a,b]
•
[a,b] ⊕[b, a] = [a + b, a +b] = [0,0]. Thus [a,b] has an additive inverse , usually called −[a,b], such that
[a,b] + (−[a,b]) = [0,0].
•
If the Chip Board with a black and b red is joined to the board with the Board with b black and a red constructs the Board with a+b black and a+b red - which is equivalent to the board with no chips (also called the Null Board).
•
For a,b ≥ 0, make the correspondences a ↔[a,0], b ↔[b,0]. Then (a + b) ↔ [a+b,0] = [a,0]⊕[b,0].
Multiplication
Indicate multiplication of equivalence classes by ⊗.
Motivated by the desired property
(a − b) ·(c −d)
= (a c + b d)−(b c + ad),
define
[a,b] ⊗[c,d]
≡ [a c + bd,b c + ad].

Chip Board. Much more complicated. The desired distributive property has a major role.
On the chip board, multiplying the Board with a black and b red by the number c, c ≥ 0 will construct the Board with a ·c black and b ·c red. I.e.,
[a,b] ⊗[c,0]
≡ [ac,bc].
Next, let us agree that multiplying by −1 should correspond to replacing every black chip by a red chip and every red chip by a black chip.† We should have that the Board with a black and b red, when multiplied by -1 should construct the board with b black and a red. Since
−1
↔ (0,1),
or −1
↔ [0,1],
we have
[a,b] ⊗[0,1]
= [b,a].
The general rule exploits the desired distributive property:
[a,b] ⊗[c,d]
= [a,b] ⊗([c,0] ⊕ [0,d])
= ([a,b] ⊗[c,0]) ⊕ ([a,b] ⊗[0,d])
= ([a,b] ⊗[c,0]) ⊕ ([a,b] ⊗(−[d,0]))
= [a c , b c]⊕[b d,a d ]
= [a c + b d, b c + ad].
There is still work to be done. We must show that the operations ⊕ and ⊗ well defined on equivalence classes. This amounts to showing that
if (a,b)
≅ (a′,b′),
and (c,d)
≅ (c′,c′),
then (a + c,b +d )
≅ (a′ +c′, b′ + d′),
and (a c + bd,b c + ad)
≅ (a′ c′ + b′d′,b′ c′ + a′d′).
Note that, for any c,
[a,b] + [c,c] = [a,b].
Thus the equivalence class [0,0] = [c,c] serves as a zero for the addition ⊕.
Also [1, 0] = [c + 1, c] serves the role of 1, the unit for ⊗:
[a,b] ⊗[1,0]
= [a ·1,b ]
= [a,b].
We identify the starting number a, a ≥ 0, with its equivalence class [a,0] = [a + c, c] (Think a = (a + c) − c.), and note that
[a + c, c] ⊕[b + d,d]
= [a + b + (c + d), c + d],
which is identified with a + b.
Also
[a + c, c] ⊕[c, a + c]
= [a + c + c, a + c + c],
= [c,c]
= Zero for ⊕.

[a , b] ⊕[b,a]
= [a +b, a + b],
= Zero for ⊕.
Now if we identify 1 with [1,0] = [c + 1, c], then its additive inverse for ⊕ is [0,1] = [c, c +1].
We can also check
[a,b] ⊗[0, 1]
= [a·0 + b ·1, a·1 + b ·0]
= [b,a].
Thus it shown that

•
The additive inverse of the unit [1,0] is [0,1],
− [1,0]
= [0,1].
•
The additive inverse of [a,b] is [a,b]⊗( additive inverse of the unit ).
− [a, b]
= (− [1,0]) ⊗[a,b].
-
Subtraction
Indicate subtraction of equivalence classes by \ominus.
Since
(a − b) − (c −d)
= (a + d) −(b + c),
define
[a,b] \ominus[c,d]
≡ [a + d,b +c]
= [a,b] ⊕[d,c]
= [a,b] ⊕(−[c,d]).
The defined subtraction, \ominus, now corresponds to the usual subtraction.


Notes

The same equivalence class construction of negative numbers could be carried out starting with the the nonnegative rational numbers or nonnegative real numbers. The role of the chips on the Chip Board might be played by colored lengths of string.
Geometric Interpretation of Equivalence Classes
Think of the pairs (a,b), a,b ≥ 0 as points in the first quadrant. Pairs of the form (a,0), a black and no red, are on the nonnegative x-axis; pairs of the form (0,b), no black and b red, are on the nonnegative y-axis.
A geometric representation of equivalence class of a pair (a,b) is all [integer] points in the first quadrant which are on the line of slope 1 through (a,b).

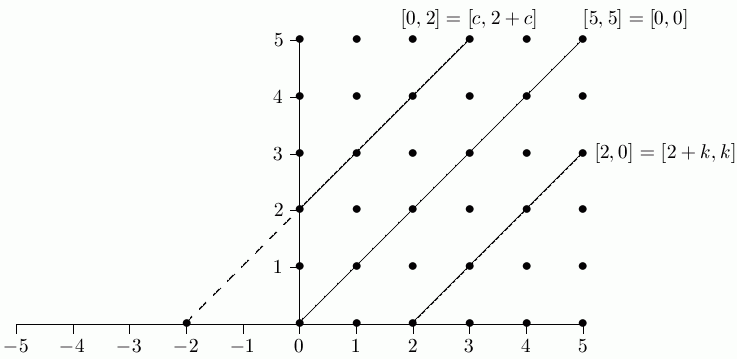
chip01.gif

Note that if we start with 2 ↔ [2,0], obtain its additive inverse [0,2], and then extend the line which represents [0,2], the line would intersect the x-axis at the point (−2,0).

Footnotes:

1I thank John Wood for his explanation of the construction in the style of Grothendieck.
† We try to force the rule (−1)[a,b] = −[a,b]

File translated from TEX by TTH, version 4.06.
On 24 May 2015, 19:12.