by Louis H. Kauffman
The author will often be designated by the word "I". I realize that nearly all that can be said of "I" is contained in the sentence: "I am the one who says I." The upshot is that every "you", including the reader of these words can also be construed as "I". I invite you to take this definition of "I" as an invitation to assume the identity indicated by that pronoun. That is, let the reference of "I" be to yourself and see if the statements are resonant for you.
The apologia: I have not taken the historical path and I have not made an exposition of the many strands of mathematics that underlie the detailed analysis of feedback and control in man and machine. In fact, what I try to do here is to start again, with the notion of systems that contain observers and systems that ARE observers, and let the mathematics unfold from that place.
Second apologia: In the next version there will be more graphics!
A cybernetic observer is wider than a physicists observer. In physics an observing system can be as simple as a record on photographic film or the reading of a needle in a gauge. A physical observing system makes a record, but is not required to reflect on that record. I, on the other hand, reflect and it is through that reflection that I can avail myself of the information in a physical record, or in a physical observing system. Of course a physical observing system may also reflect.
In doing mathematics it appears to be necessary to have a physical record for drawing images, symbols and calculations. A stick and a tide-flattened stretch of sand will suffice. A word-processor and allied graphics facilities will do as well.
Mathematics commonly begins with formalisms. Here I start before the advent of formalism and discuss the prerequisites. Those prerequisites are the prerequisites for communication. They are, for example, the very same prerequisites as the prerequisites for notating music or writing the script of a play.
Mathematics proceeds by series of injunctions, as in a recipe. Mathematics transcends the simple domain of recipes by allowing reflection on the structure of the recipe to become part of the mathematics.
For example, suppose that SUM = 1 + X + X*X + X*X*X + ....
Then SUM = 1 + X*(1 + X + X*X + ...).
Hence SUM = 1 + X*SUM.
(X*Y denotes the product of X and Y.) By reflecting on the algorithm (recipe) of summing the powers of a number X, we see that the algorithm reflects into ITSELF yielding a self referent equation for the SUM. This can be solved SUM = 1 + X*SUM
SUM - X*SUM = 1
SUM*(1- X) = 1
SUM = 1/(1 - X).
The interpretation of this result depends upon the numerical domain in which you work. Many people would accept that 2 = 1 + (1/2) + (1/2)*(1/2) + ... .
and deny that 1/2 = 1-1+1-1+1-1+1-... .
The interpretation of the solution of a self-referent equation is a matter of context. The mathematician can remain separated from the mathematics only at the cost of incoherence in the face of self-reference.
Algebra is a domain in which I can reflect on the structure of arithmetic. Is there a mathematical domain in which I can reflect on reflection? If so, then such a domain could be the basis for a cybernetics of observing systems. Let us look for such a domain.
Mathematics is based on the notion of distinction. Mathematics is the study of what there would be if there could be anything at all.
In set theory the most elementary explicit distinction is the empty set, symbolized by the empty container { }. (The empty set is a logical precursor to the making of zero in arithmetic.) The operation of forming a set is an operation that makes the distinction that is the contents of the set. This gives rise at once to a vast hierarchy of sets obtained from nothing. First there is the empty set { }, then the set whose member is the empty set { { } }, then the set whose members are the empty set and the set consisting of the empty set { { }, { { } } } , and so on. This particular form of creating distinctions is not the only way to proceed, but must be mentioned particularly for the fundamental recursion (due to John von Neumann).
S(0) ={}
S(n+1) = { all previously created sets}.
Thus S(1) = { {} }
S(2) = { {} , { {} } }
S(3) = { {} , { {} }, { {} , { {} } } }
...
Any two empty sets have the same members (none!). With the definition that two sets are equal only if they have the same members, I get at once that the empty set is unique and that S(n) has n distinct members.
By already knowing the domain of numbers and by going to the realm of sets and their creation we see that multiplicity arises of its own accord under the conditions of set-formation. The conditions of set-formation are in fact a reflection of my ability to reflect. That is, the act of forming a set is a formal image of the act of "thinking about" a given domain. The von Neumann recursion is an image of thinking about thinking.
Why then has there been a prohibition against sets that are members of themselves, or against sets that are members of each other? (This is explicitly disallowed by the foundation axiom in classical set theory. Recent theories such as those of Aczel do allow self-membership.) The common answer is that such sets (that are members of themselves) lead to the Russell paradox of the set R of all sets that are not members of themselves. (Is R a member of itself? If Yes then No. If No then Yes.) In the next section we shall see that knots give a very clean way to think about sets that are members of themselves.
As far as the Russell paradox is concerned, its resolution depends upon your point of view. I like to think of my sets as evolutionary. The Russell set changes as soon as you insert it into itself. The new Russell set still does not contain IT-self. The dog chases its tail. The paradox creates time and then there is no paradox.
Unless you prohibit it, self-reference occurs naturally in mathematics. Infinity and self-reference are synonymous in the following sense. Suppose we write a self-referential equation such as A = *A.
Then this equation becomes a rule for substitution: A=**A=***A=****A=*****A= ... .
Thus the self-reference leads to an infinite process. The results of this process tend to have a pattern of invariance that approximates the self-reference itself. Thus a row of 100 stars looks approximately like a row of 101 stars. This leads to possibly nonsensical notions such as an infinite row of stars
INFINISTAR = ********************************************...
I would like INFINISTAR to have an "existence" so that, literally *INFINISTAR=INFINISTAR.
The existence of INFINISTAR is certainly not a physical existence in any sense that we can construct. I mean, nobody and no computer can lay down an infinite row of stars. INFINISTAR is a CONCEPT. It is the concept that you can always add one more star. And it is a true concept, as you can verify for yourself. If you are present before a row of stars, then you can add one more star. If you are present and distinguishing, then you can make one more distinction. Being present and distinguishing is a process. I am not stopped. If I am stopped, then I am not and there is no one and there is nothing to discuss.
There IS a problem with the usual formulation of set theory. That problem is that all the created sets are assumed to be present in eternity. They are regarded as existences rather than as processes. But that problem is also the virtue of the classical theory because many sets (processes though they really are) have the capacity to keep recreating themselves in the eye of the observer as apparently unchanged. Von Neumann's numbers S(0), S(1), ... have this capacity, and so form the backbone of number theory and give it that quality of eternal existence that motivated the mathematician G.H. Hardy to exclaim that mathematical existence was firmer than physical existence.
All around the relatively static mathematical entities are self-referential entities that propel themselves forward into time and cross the boundaries between the observer of the mathematics and the mathematics itself. By starting with a distinction rather than a set, we recognise the circular and self-referential nature of the mathematics from the outset and allign it directly with cybernetic thinking.
Self-reference does not require physical infinity to bring it into existence. Self-reference has conceptual life. Nothing brings this more clearly to the fore than just understanding that you yourself make the distinctions that allow your own cognition. It is amusing and useful to see this process reflected in formalism. Allow me to introduce you to the DUPLICATING GREMLIN, G. When G meets an object on its right it duplicates the object and puts it in brackets so: GQ = [ QQ ].
Now suppose we go to the Gremlin Factory, purchase two duplicating gremlins and introduce them to each other. Then GG = [ GG ] and we see that the "entity" GG is self-referential.
Of course "equals" here means "can be substituted for" and the equation GG = [ GG ] initiates the process GG = [ GG ] = [ [ GG ] ] = ...
This form of self-reference is the basis of recursive programming and was first articulated by Church and Curry in the form of the lambda calculus for mathematical logic. The same pattern of self-reference underlies the structure of Godel's incompleteness theorem and many other constructions in logic and mathematics.
In fact, we can generalize the gremlin in the following way. Let Gx = F(xx) for any F. Then GG=F(GG).
We see that "any" F has a fixed point GG. I have been utterly cavalier about specifying the domain of applicability of F. It is at this level that we arrive at a parallel with the notion of the self. For I am indeed utterly cavalier in specifying the domain of application of the self, and in that way I become the fixed point of that self that is myself.
This is a good point to end this brief introduction to the mathematics of "second-order" cybernetics.

The knot itself is a pattern that intermediates between the rope (substrate) and the ambient space (context). The knot cannot exist without the rope and the space. Once knotted, the pattern, which might be thought of as imposed on the rope, is an integral part of the physicality of the "rope-in-space". The boundary between the object and its description has disappeared. This is the real disappearing rope trick.
Now imagine a simple loop of rope. Allow that when a bit of line passes underneath another bit of line, we shall say that the underpassing bit "belongs" to the overpassing bit. Membership by underpassage.
The simple loop is then an empty "knot set". Put a twist in the loop and it underpasses itself. The singly twisted loop is a member of itself. Loop and twisted loop are topologically equivalent. Hence, speaking {topo}logically, the simple loop is both a member of itself and not a member of itself. By this simple twist of logic, the paradox becomes a phenomenon of three dimensional space.
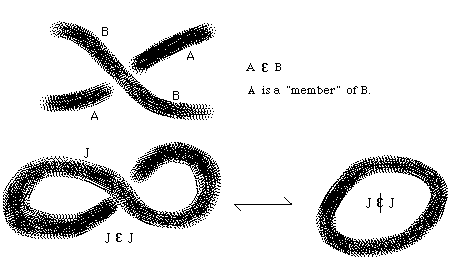
In Space the knots and links are WHOLE FORMS without any parts. In the projections of the knots and links to a plane I see them cut up into parts that are arranged self-referentially. A system that has a self-referential description can be construed as a projection of a system that is WHOLE in a higher dimensional space. The self-reference is seen as an illusion of the projection. Any particular decomposition of the system into parts is a case of this illusion. It is an illusion exactly analogous to the forming of coordinates for the "locations" of the "points" of an "object" in ordinary space.
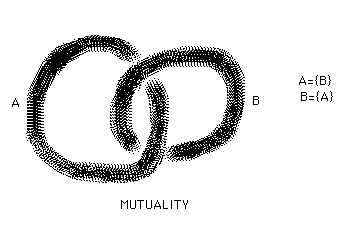
Consider two linked loops, each linking the other once. Call the loops A and B. Then in a pictorial representation, A passes once under B and B passes once under A. Thus B={A} and A={B}. The linkage corresponds to a mutuality in knot sets.
One point that is worth mentioning before we close is that knots lead naturally to "quantum networks". In a quantum network signals are not passed as in an electrical network. Rather, the network has states with values in a numerical domain such as the complex numbers. An "amplitude" is associated with the net as the sum over all the values of the states. This amplitude corresponds to the probability for occurence of the process that is the net. The quantum nets are circularly interconnected but the quantum amplitudes measure this interconnectedness without the paradoxes of recursion. In the next installment we shall discuss the relevance of this point of view with cybernetic analysis of systems, languages and conversations.