Cycles in a Graph and the Field Z/2Z

by Louis H. Kauffman

These notes are designed to teach you how to use linear algebra to find all the cycles in a graph. A cycle in a graph is a set of edges that form a pathway starting at some vertex and eventually returning to the same vertex. In the course of traversing the path, each edge of the cycle is used exactly once. Some vertices may be visited more than once in the course of going around the cycle.

You have already met the concept of cycle in a graph in solving the linear equations for finding the current in an electrical graph.

Here is a graph G:

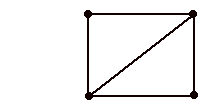
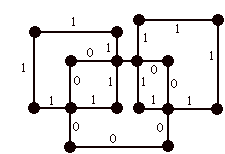
There are three cycles in G, indicated below by copies of G where the edges of a cycle have 1's as labels and the remaining edges have 0's as labels.

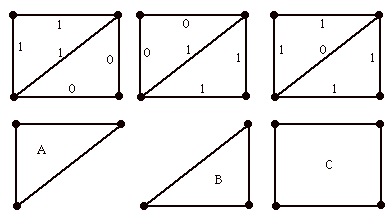
Beneath each copy of the graph with the labeled cycle is a depiction of just those edges of G that form the cycle. Thus we see that in this graph G the cycles consist in two triangles and one rectangle. We have named these cycles A, B and C for the sake of further discussion.

Now we will encode each of the cycles as vectors with entries that are either zero or one. To do this we think of any labeling of the graph G as a vector of the form V = (x,y,z,w,t) where the letters x, y, z, w, t refer to the edges of the graph as shown below.

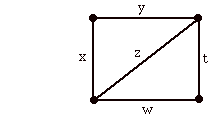
Thus we see that

A=(1,1,1, 0,0)

B= (0,0,1,1,1)

C = (1,1,0,1,1)

by referring to the previous figure.

The main point about a cycle encoded as a vector is that each vertex of the graph contributes an even number of ones to this vector (possibly none). Consider the following example.

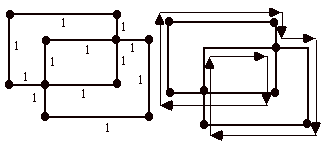
In this example we have indicated that the whole graph consists in the cycle. Certainly every vertex is contributing an even number of ones. But also we have indicated a pathway on the graph that should convince you that it makes sense to think of the graph itself as a cycle (in the sense of a pathway that returns to itself). Note also that there is more than one way to make such a pathway. For this reason it is convenient to DEFINE a cycle to be a labeling of a subset of the edges of the graph with ones, such that every vertex sees an even number of ones. With the definition some cycles are really disjoint unions of cycles such as the example below.

In this example there are two clearly marked (by ones) disjoint cycles. The corresponding vector is the sum of these two individual cycles. It is only a slight abuse of terminolgy to call a sum of geometric cycles a cycle, and we shall speak in just this way.

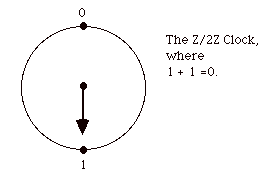
We will be doing our vector algebra for cycles in a graph over the very simple arithmetic of the field Z/2Z = {0,1}. In this arithmetic

1 + 1 = 0.

This means that the arithmetic in Z/2Z is like that for a clock that only indicates two times: 0 and 1.

Now take note what this means. If 1 +1 =0 then 2=0 and

-1 = 1. So arithmetic is made incredibly simple. The only values are zero and one.

Lets add the vectors A and B over Z/2Z:

A + B = (1,1,1,0,0) + (0,0,1,1,1) = (1+0, 1+0, 1+1, 0+1,0+1)

= (1,1,0,1,1) = C.

Thus A + B = C.

Over Z/2Z the sum of two cycles turns out to be another cycle!

Note that B + C = (0,0,1,1,1) + (1,1,0,1,1) = (1,1,1,0,0) = A and that

A + C = B.

This notion of algebraic addition of cycles over Z/2Z corresponds to the geometric idea of addtion of cycles where common edges cancel. See the figure below for an illustration of this idea.

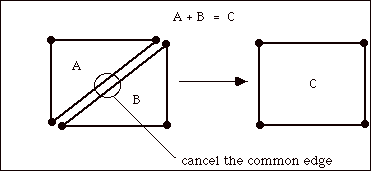
Notice also that if you superimpose A and C and cancel the common edges, you will obtain B.

With these ideas about cycles and vectors over Z/2Z in hand we can use linear algebra to search for the cycles in a graph by writing down a system of equations corresponding to the graph and then solving these equations over Z/2Z. The basic perscription for the system of equations is the following: FOR EACH VERTEX IN THE GRAPH WRITE AN EQATION THAT STATES THAT THE SUM OF THE LABELS AT THAT VERTEX IS EQUAL TO ZERO IN Z/2Z. This stipulation means exactly that the number of ones that occur at that vertex is even, and this is just what we mean by a cycle (in the light of the discussion above).

Here is an example.

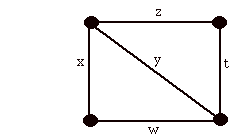
The cycle equations for this graph are

x+y+z=0

w+y+t=0

x+w = 0

z+t = 0.

Note that these are equations written about w,x,y,z,t in Z/2Z.

We can write the matrix for this system and row reduce it over Z/2Z.

The matrix is

w x y z t

0 1 1 1 0

1 0 1 0 1

1 1 0 0 0

0 0 0 1 1

We first intercange the first and second rows to obtain

w x y z t

1 0 1 0 1

0 1 1 1 0

1 1 0 0 0

0 0 0 1 1

Then we add the first row to the third row in Z/2Z:

w x y z t

1 0 1 0 1

0 1 1 1 0

0 1 1 0 1

0 0 0 1 1

Now add the second row to the third row.

w x y z t

1 0 1 0 1

0 1 1 1 0

0 0 0 1 1

0 0 0 1 1

Now add the third row to the fourth row.

w x y z t

1 0 1 0 1

0 1 1 1 0

0 0 0 1 1

0 0 0 0 0

Now add the third row to the second row.

w x y z t

1 0 1 0 1

0 1 1 0 1

0 0 0 1 1

0 0 0 0 0

This last matrix is in row echelon form, and we can write the solution in terms of the pivot columns corresponding to w,x and z with independent variables y and t:

w = y+t

x = y + t

z= t

Hence

(w,x,y,z,t) = (y+t, y+t, y,t,t) = y(1,1,1,0,0) + t(1,1,0,1,1).

Since y and t can be either 0 or 1, this means that we get exactly three solutions:

A= (1,1,1,0,0)

C= (1,1,0,1,1)

and

B = A+C= (1,1,1,0,0)+(1,1,0,1,1) = (0,0,1,1,1).

Here we have used the names of these cycles as they appeared in an earlier example above (but the pictures are turned around from one example to the other so take care in making a direct comparison!).

This method of calculating cycles can be used to good effect in larger graphs.

Exercises.

Solve the system of cycle equations over Z/2Z for the following graphs.

1.

2.

3.

Note that this last graph hs six vertices and that we have drawn some of the edges with corners.