by Louis H. Kauffman
A Fourier knot is a knot that is described by equations in cartesian coordinates x,y,z of the form
where f(t), g(t) and h(t) are Fourier series with finitely many terms. The game is more interesting with finite Fourier series, since any knot can be so represented topolgically, and it is a good puzzle to find simplest representations.
An excellent class of Fourier knots are the so-called Lissajous knots. A Lissajous knot has equations in the form
where n,m,p are integers. In the paper by Bogle, Hearst, Jones and Stoilov { "Lissajous Knots", Journal of Knot Theory and Its Ramifications, Vol.3, No. 2 (June 1994), pp. 121- 140} these knots are studied, and it is proved that a Lissajous knot always has Arf invariant equal to zero. The Arf invariant is a venerable invariant of knots that divides them into two classes. The simplest knot, the trefoil, has Arf invariant equal to one. Thus the trefoil is not a Lissajous knot.
In this note we give what may be the first and possibly the simplest Fourier version of the trefoil knot. The equations are as follows.
The figure below shows a rendering of these equations.
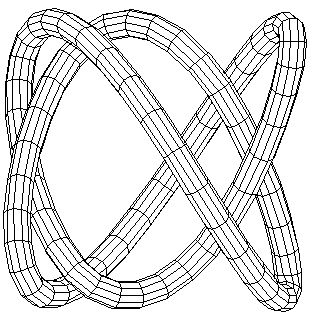
In this Figure we see easily how the Fourier Trefoil projects to a Lissajous Figure of type (2,3) in the plane, yet the knot itself is not a Lissajous knot.
It is fascinating to compare the Fourier Trefoil with "The Pattern" of Lynnclaire Dennis. The Pattern is a trefoil knot seen as an orbit about a central sphere. The orbit is more symmetrical than this initial version of a Fourier trefoil. We are working on locating the simplest Fourier trefoil that will give a good version of The Pattern.
The work of Aaron Trautwein takes the subject of Fourier or Harmonic knots to another level by using this concept to find equations for large classes of knots in extremal energy forms. Trautwein's techniques in conjunction with the energy work of Jon Simon and the computer program "Ming" written by Ying-Qing Wu mark the beginnings of a new approach to the theory of knots through physical and computer representations.
For the work of Bob Gray on the geometry of the Pattern see Bob Gray's Geometry where he has beautiful computer graphics of the polyhedral spheres related to the pattern, animations of torus knots and more.
This is work in progress by SAM. SAM = Science + Art + Mathematics. For more information about Fourier Knots, see my paper Fourier Knots.