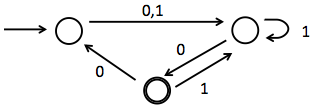
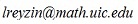Syllabus: pdf
|
|
Time and Location: M-W-F 12:00-12:50pm, Taft Hall (TH) 320
|
|
Instructor Contact Information: Lev Reyzin, SEO 713, (312)-413-9576, |
|
|
Textbook: M. Sipser,
Introduction to the Theory of Computation, 3rd edition
|
|
Office Hours: T-F 2:00-3:00pm, or by appointment
|
|
Exam Dates
Midterm 1: 2/20/13, during classtime
Midterm 2: 3/15/13, during classtime
Final Exam: 5/7/2013, 8-10am
Problem Sets
Problem Set 1: pdf, due 1/23/13
Problem Set 2: pdf, due 2/1/13
Problem Set 3: pdf, due 2/8/13
Problem Set 4: pdf, due 2/18/13
Problem Set 5: pdf, due 2/27/13
Problem Set 6: pdf, due 3/8/13
(Turing's paper)
Problem Set 7: pdf, due 3/13/13
(Aaronson's article)
Problem Set 8: pdf, due 4/5/13
Problem Set 9: pdf, due 4/19/13
Problem Set 10: pdf, due 5/1/13
Lectures and Readings
Note: lectures will have material not covered in the readings.
Lecture 1 (1/14/13)
covered material: intro to the course, overview of prerequisite
material
reading: chapter 0
Lecture 2 (1/16/13)
covered material: intro to DFAs: examples, their formal description,
defining computation
reading: begin chapter 1.1
other: problem set 1 given out
Lecture 3 (1/18/13)
covered material: designing DFAs, intro to regular operations
reading: continue chapter 1.1
Lecture 4 (1/23/13)
covered material: regular languages closed under union and
intersection, intro to NFAs
reading: finish chapter 1.1, begin chapter 1.2
Lecture 5 (1/25/13)
covered material: NFA and DFA equivalence, regular languages closed
under concatenation and star
reading: finish chapter 1.2
other: problem set 2 given out
Lecture 6 (1/28/13)
covered material: introduction to regular expressions, converting
regular expressions to NFAs
reading: begin chapter 1.3
Lecture 7 (1/30/13)
covered material: defining GNFAs, converting DFAs to GNFAs
reading: finish chapter 1.3
Lecture 8 (2/1/13)
covered material: converting GNFAs to REs, introduction to
non-regular languages
reading: begin chapter 1.4
other: problem set 3 given out
Lecture 9 (2/4/13)
covered material: enumerability of regular languages,
diagonalization on all languages, pumping lemma
reading: continue chapter 1.4
Lecture 10 (2/6/13)
covered material: pumping lemma proof, applying it
to show languages are not regular
reading: finish chapter 1
Lecture 11 (2/8/13)
covered material: intro to CFGs and CFLs, their formal definition,
that RLs are a proper subset of CFLs
reading: begin chapter 2.1
other: problem set 4 given out, first midterm announced
to take place on 2/20/13 in class
Lecture 12 (2/11/13)
covered material: ambiguous grammars, inherently ambiguous
languages, CNF, testing CFG membership
reading: finish chapter 2.1
Lecture 13 (2/13/13)
covered material: defining PDAs, an example, discussion of
nondeterminism in pushdown automata
reading: begin chapter 2.2
Lecture 14 (2/15/13)
covered material: designing and interpreting PDAs
reading: continue chapter 2.2
Lecture 15 (2/18/13)
covered material: CFG and PDA equivalence,
intro to pumping lemma for CFLs
reading: finish chapter 2.2, begin chapter 2.3
other: midterm Wednesday!
Lecture 16 (2/20/13)
midterm exam 1, no lecture
other: problem set 5 given out
Lecture 17 (2/22/13)
covered material: proof of pumping lemma for CFLs,
applications to show languages are not context-free
reading: finish chapter 2.3
Lecture 18 (2/25/13)
covered material: closure properties for CFLs,
introduction to Turing Machines
reading: begin chapter 3.1
Lecture 19 (2/27/13)
covered material: designing TMs, state diagrams
of TMs, defining decidable and recognizable languages
reading: finish chapter 3.1
Lecture 20 (3/1/2013)
covered material
multi-tape TMs, nondeterministic TMs, Enumerators,
and equivalence to TMs
reading: chapter 3.2
other: problem set 6 given out
Lecture 21 (3/4/2013)
covered material:
Hilbert's 10th problem, Church-Turing thesis, some
closure properties of decidable languages
reading: chapter 3.3