Math 205 Exam II Solutions (part 1)
Lowman Fall 2005
- Put your TA's name and your name on the exam booklet.
- Show your work for each problem in the exam booklet.
- When possible, you can leave your answers in terms of the symbol e, factorials, fractions etc.
However, you must make obvious
simplifications.
P1 (10pts)
A study of the people in a region showed that 40% were smokers.
The probability of death due to lung cancer, given that a person
smoked, was 20 times the probability of death due to lung cancer, given
that the person did not smoke. If the probability of death due to
lung
cancer in the region is .01, what is the probability of death due
to lung cancer given that the person is a smoker?
Solution:
P(S) = .4
P(D|S) = 20 * P(D | notS)
P(D) = .01
P(D|S) = ?
---------------------------------------------------------------------
Event composition method:
P(D) = P(D and S) + P(D and notS)
= P(S) * P(D|S) +
P(notS) * P(D | notS)
.01 = (.4) * P(D|S) + (1 - .4) * ( P(D|S) / 20 )
.01 = (.4 + .6/20) * P(D|S)
.01 = .43 * P(D|S)
P(D|S) = .01 / .43 = 1/43 = 2.3%
note: P(D| notS) = 1/20 * 1/42 = 1 / 840 = .1%
P2 (10pts)
A lie detector will show a positive reading (indicate a lie ) 10% of
the time when a person is telling the truth and 95% of the time when
the person is lying. Suppose two people are suspects in a one-person
crime
and (for certain) one is guilty. What is the probability that the
detector shows a positive reading for at least one of the suspects?
Solution:
First find a process that could represent the experiment. One possible
process would be to first give the lie detector test to the guilty
person(who will lie) and then give the test to the innocent person(who
will tell the truth. Each outcome can then be represented as an ordered
pair. With the first part of the pair is the test results for the
guilty person and the second part the test results for innocent
person. A tree can be used to list all outcomes and assign
probabilities. It is assumed that the test results for the guilty
person are independent from the results for the innocent person.
Therefore, conditional probabilities are not need for the second
branches of the tree.
---tree---
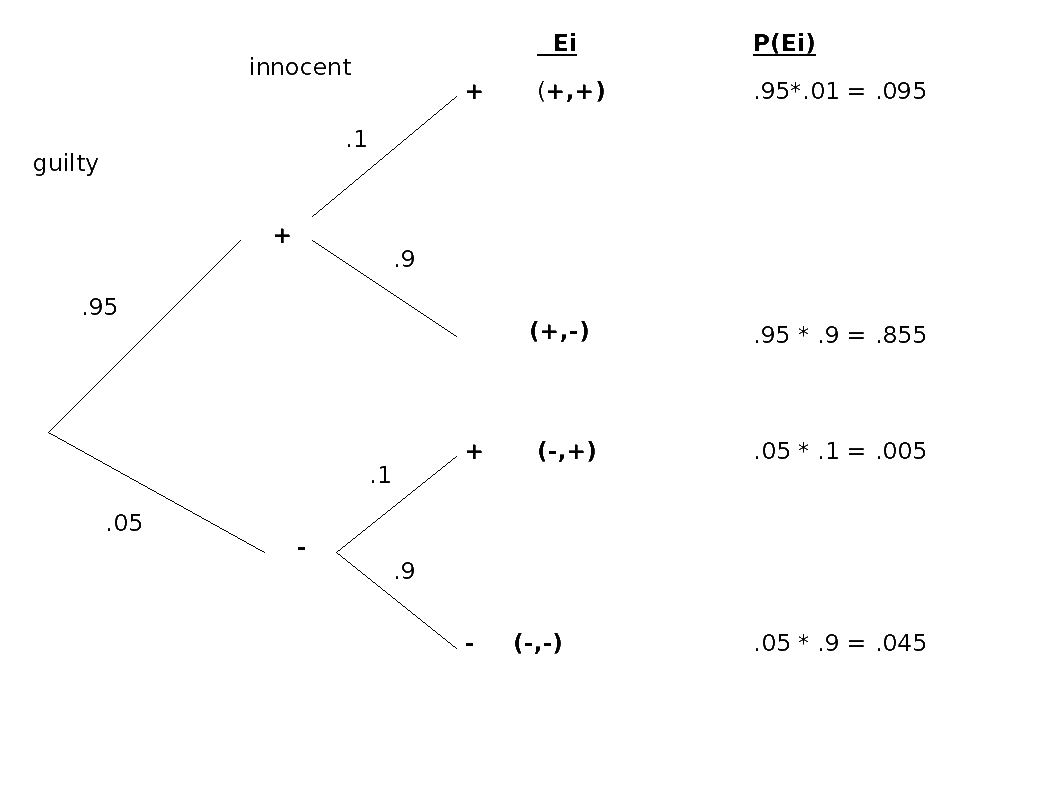
What is the probability that the detector shows a positive
reading for at least one of the suspects?
P = P( {(+,+), (+,-), (-,+) ) = .095 + .855 + .005 = .9550
alternate metnod:
P = 1 - P(neg for both) = 1 - P( -,- ) = 1 - .045 = .955
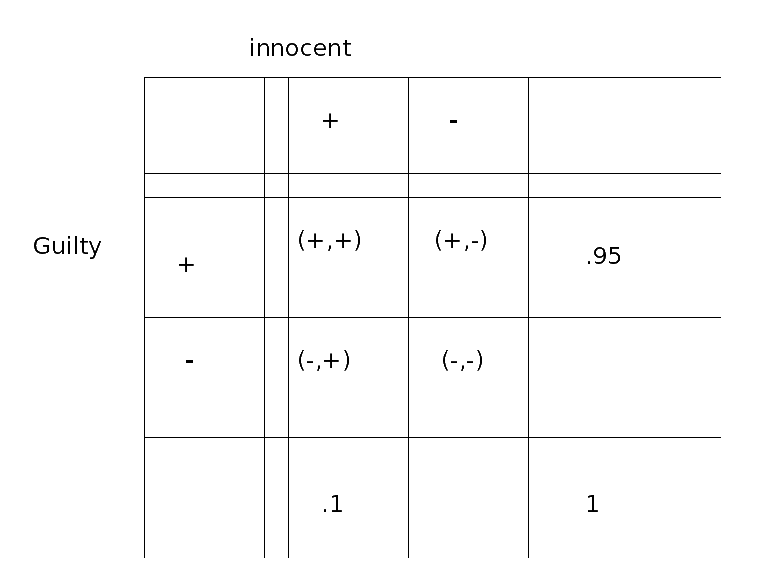
Because the test results are independent of who took the test, A table
or Venn diagram could also be used.
---table-----------
First set up a table of outcomes with the given probabilities:
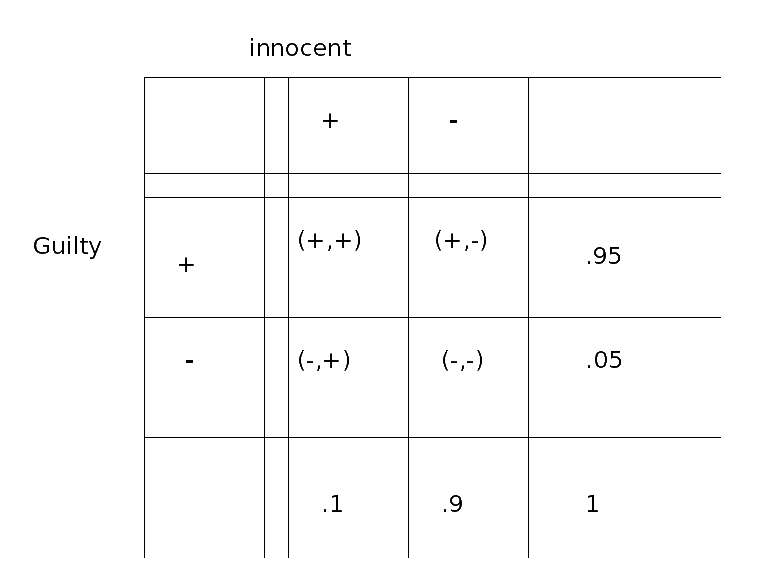
Second, calculate the missing marginal probabilities:
Third, since the test results are independent, the probabilies of each
cell can be found by multiplying the two corresponding marginal
probabilities.
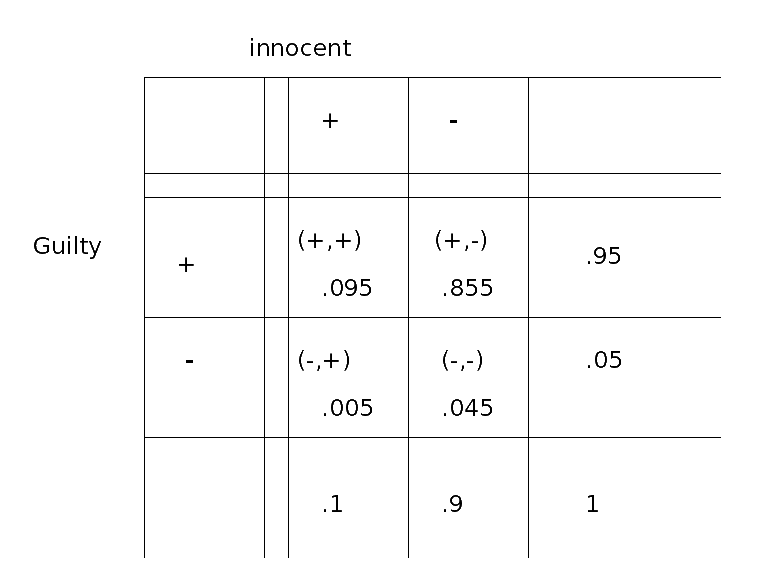
From here you continue the same as when using the tree.
-------end table---------------
Another very simple way to
solve the problem is:
P(atleast one +) = 1 - P( both -) = 1 - P(-,-) = 1 - P( - | lies) * P(
- | tells truth) = 1 - (.05)* (.9) = .955
--------------------end problem
2------------------------------------------------
P3 (20pts)
A sales person can contact either zero, one or two customers per day
with probabilities 1/6, 2/6 and 3/6 , respectively.
Each contact
will result in either no sale or a $1,000 sale with probabilities
0.8 and
0.2. (a) Give the probability distribution for daily sales in the form
of
a table and (b) Find the mean and (c) set up the calculation to find
the
variance of daily sales. You do not need to find the actual number,
just set up
the calculation.
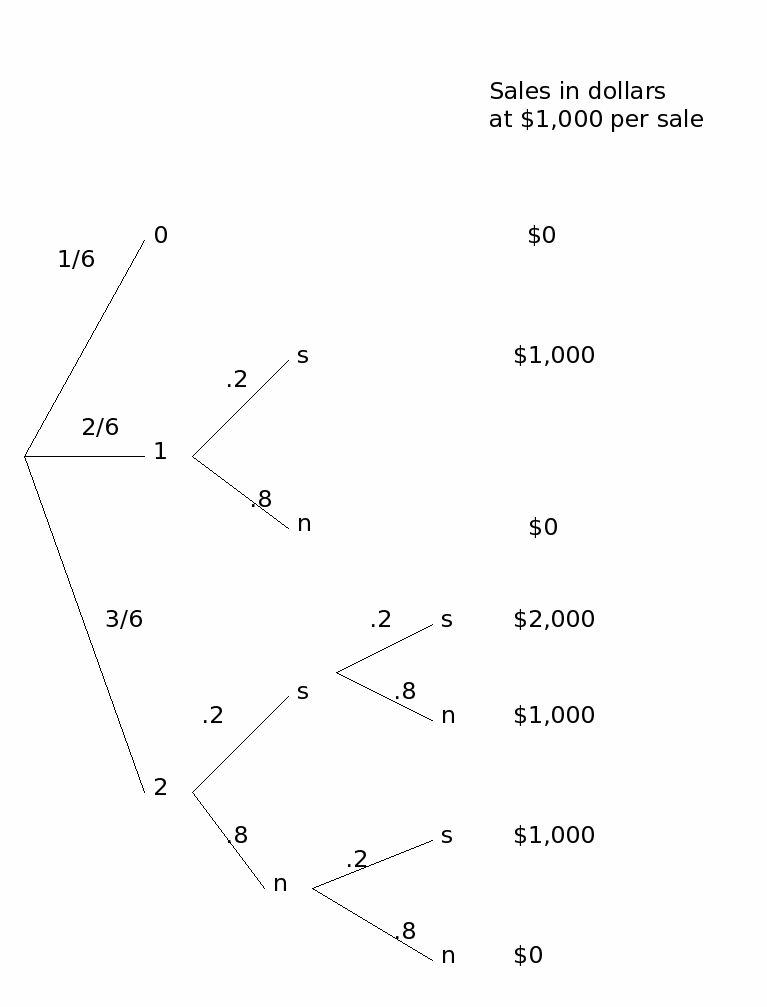
(a) Probability distribution for X.
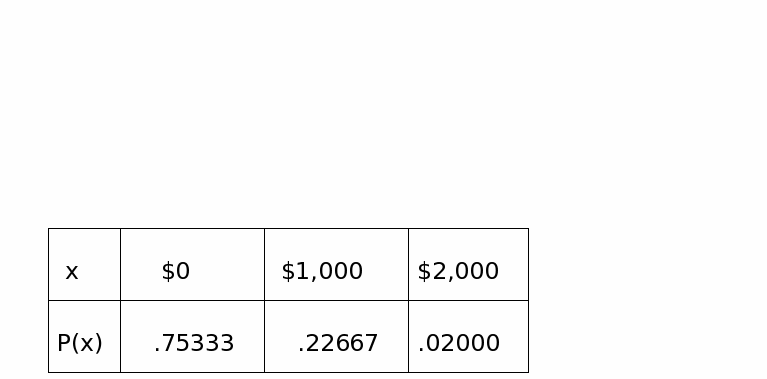
(b) E(x) = $0 * (.75333) + $1,000 * (.22667) + $2,000 * (.02) = $266.67
(c) check later.
===============================================================
===============================================================






