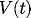 measure the size of the tumor
(e.g. volume, number, etc.). The
Gompertz growth law is described by the following system
of differential equations:
measure the size of the tumor
(e.g. volume, number, etc.). The
Gompertz growth law is described by the following system
of differential equations:
The Gompertz growth law has been shown to provide a good
fit for the growth data of numerous tumors.
Let
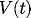 measure the size of the tumor
(e.g. volume, number, etc.). The
Gompertz growth law is described by the following system
of differential equations:
measure the size of the tumor
(e.g. volume, number, etc.). The
Gompertz growth law is described by the following system
of differential equations:
![\[ \frac{dV}{dx} = r(t)V(t), \;\; V(0)=V_0 \]](gompertz_2.gif)
![\[ \frac{dr}{dx} = \alpha r(t), \;\; r(0)=\beta \]](gompertz_3.gif)
Here
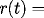 tumor growth rate
tumor growth rate
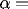 retardation constant
retardation constant
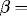 initial growth or regression rate.
initial growth or regression rate.
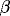 determines where the tumor grows
or regresses.
The solution is given by
determines where the tumor grows
or regresses.
The solution is given by
![\[ V(t)=V_0 e^{\displaystyle \frac{\beta}{\alpha}
(1-e^{-\alpha t})} \]](gompertz_8.gif)
where the constants are determined by the data.
In the serial treatment model discussed in class, we assume that the post-treatment tumor has the same growth characteristics as the original tumor. Specifically, we assume that the ultimate tumor size remains the unchanged which we denote as:
![\[ \theta = V_0 e^{\beta/\alpha} \]](gompertz_9.gif)
The Gompertz growth model can be written in the following form:
![\[ \frac{dV}{dt} = - \alpha V \ln \left(\frac{V}{\theta}\right). \]](gompertz_10.gif)
To determine the tumor regression from just before one treatment to just before the next, we integrate the first order differential equation as follows (see figure in the exponential case)
![\[ \int_{FV_n}^{V_{n+1}} \frac{dV}{\ln \left(\frac{V}{\theta}\right)}=
\int_0^T \alpha dt \]](gompertz_11.gif)
This leads to the difference equation
![\[ \ln \left(\frac{V_{n+1}}{\theta}\right) =
\ln \left(\frac{F \ V_n}{\theta}\right)e^{-\alpha T} \]](gompertz_12.gif)