The artificial-parameter homotopy

The artificial-parameter homotopy has the following form:

$$H({\bf x},t) = a (1-t)^k Q({\bf x}) + t^k P({\bf x}), \quad t \in [0,1],$$

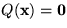with $Q({\bf x}) = {\bf 0}$ a start system, and $P({\bf x}) = {\bf 0}$ the target system.

The homotopy parameter k 

determines the power of the continuation parameter t. Taking k>1 has as effect that at the beginning and at the end of the continuation, changes in t do not change the homotopy as much as with a homotopy that is linear in t so that paths are better to follow. The default value k=2 is recommended.

The homotopy parameter a 

ensures the accessibility and regularity of the solution paths, i.e.: by choosing a random complex number for a, all paths are regular and do not diverge for t<1.

The target value 

for the continuation parameter t is by default 1. To create stepping stones in the continuation stage, it is possible to let the continuation stop at t<1, for instance at t = 0.9 or even at a complex value for t. The solutions at t<1 will serve at start solutions to take up the continuation in a later stage. In this stage, the same homotopy parameters k and a must be used.

A projective transformation 

of the homotopy and start solutions makes the equations in the polynomials homogeneous and adds a random hyperplane. The vectors of the start solutions are extended with an additional unknown. For solutions at infinity, this additional unknown equals zero.