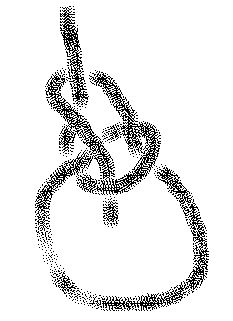
KNOTS
by Louis H. Kauffman
CONTENTS
I. Preface
II. Knot Tying and the Reidemeister Moves
III. Invariants of Knots and Links - A First Pass
IV. The Jones Polynomial
V. The Bracket State Sum
VI. Vassiliev Invariants
VII. Vassiliev Invariants and Lie Algebras
VIII. A Quick Review of Quantum Mechanics
IX. Knot Amplitides
X. Topological Quantum Field Theory - First Steps
I. Preface
This essay constitutes an introduction to the theory of knots as it has been influenced by developments concurrent with the discovery of the Jones polynomial in 1984 and the subsequent explosion of research that followed this signal event in the mathematics of the twentieth century.
I hope to give the flavor of these extraordinary events in this exposition. Even the act of tying a shoelace can become an adventure. The familiar world of string, rope and the third dimension becomes an inexhaustible source of ideas and phenomena.
As indicated by the table of contents, Sections 2 and 3 constitute a start on the subject of knots. Later sections introduce more technical topics. The theme of a relationship of knots with physics begins already with the Jones polynomial and the bracket model for the Jones polynomial as discussed in Section 5. Sections 6 and 7 provide an introduction to Vassiliev invariants and the remarkable relationship between Lie algebras and knot theory. The idea for the bracket model and its generalisations is to regard the knot itself as a discrete physical system - obtaining information about its topology by averaging over the states of the system. In the case of the bracket model this summation is finite and purely combinatorial. Transpositions of this idea occur throughout, involving ideas from quantum mechanics (Sections 8 and 9 ) and quantum field theory (Section 10 ). In this way knots have become a testing ground not only for topological ideas but also for the methods of modern theoretical physics.
This essay concentrates on the construction of invariants of knots and the relationships of these invariants to other mathematics (such as Lie algebras) and to physical ideas (quantum mechanics and quantum field theory). There is also a rich vein of knot theory that considers a knot as a physical object in three dimensional space. Then one can put electrical charge on the knot and watch (in a computer) the knot repel itself to form beautiful shapes in three dimensions. Or one can think of the knot as made of thick rope and ask for an "ideal" form of the knot with minimal length to diameter ratio. There are many aspects to this idea of physical knots. It is a current topic of my own research and the research of many others. I wish that there had been space in this essay to cover these matters. That will have to wait for the next time!
In the meantime, it gives me great pleasure to thank Vaughan Jones, Ed Witten, Nicolai Reshetikhin, Mario Rasetti, Sostenes Lins, Massimo Ferri,Lee Smolin,Louis Crane,David Yetter, Ray Lickorish, DeWitt Sumners,Hugh Morton, Joan Birman, John Conway, John Simon and Dennis Roseman for many conversations related to the topics of this paper. This research was partially supported by the National Science Foundation Grant DMS -2528707.
II. Knot Tying and the Reidemeister Moves
For this section it is recommended that the reader obtain a length of soft rope for the sake of direct experimentation.
Figure 1 - The Bowline
In showing the bowline we have drawn it loosely. To use it, grab the lower loop and pull it tight by the upper line shown in the drawing. You will find that it tightens while maintaining the given size of the loop. Nevertheless, the knot is easily undone, as some experimentation will show.
The utility of a schema for drawing a knot is that the schema does not have to indicate all the physical properties of the knot. It is sufficient that the schema should contain the information needed to build the knot. Here is a remarkable use of language. The language of the diagrams for knots implicitly contains all their topological and physical properties, but this information may not be easily available unless the "word is made flesh" in the sense of actually building the knot from rope or cord.
Our aim is to get topological information about knots from their diagrams. Topological information is information about a knot that does not depend upon the material from which it is made and is not changed by stretching or bending that material so long as it is not torn in the process. We do not want the knot to disappear in the course of such a stretching process by slipping over one of the ends of the rope. The knot theorist’s usual convention for preventing this is to assume that the knot is formed in a closed loop of string. The trefoil knot shown in Figure 2 is an example of such a closed knotted loop.

Figure 2 - The Trefoil as Closed Loop
A knot presented in closed loop form is a robust object, capable of being pushed and twisted into many topologically equivalent forms. For example, the knot shown in Figure 3 is topologically equivalent to the trefoil shown in Figure 2.
The existence of innumerable versions of a given knot or link gives rise to a mathematical problem. To state that a loop is knotted is to state that nowhere among the infinity of forms that it can take do we find an unkotted loop. Two loops are said to be (topologically) equivalent if it is possible to deform one smoothly into the other so that all the intermediate stages are loops without self intersections. In this sense a loop is knotted if it is not equivalent to a simple flat loop in the plane.
The key result that makes it possible to begin a (combinatorial) theory of knots is the Theorem of Reidemeister [REI] that states that two diagrams represent equivalent loops if and only if one diagram can be obtained from the other by a finite sequence of special deformations called the Reidemeister moves.
I shall illustrate these moves in a moment. The upshot of Reidemeister’s Theorem is that the topological problems about knots can all be formulated in terms of knot diagrams.

Figure 3- Deformed Trefoil
There is a famous philosophy of mathematics called "formalism", in which mathematics is considered to be a game played with symbols according to specific rules. Knot theory, done with diagrams, illustrates the formalist idea very well. In the formalist point of view a specific mathematical game (formal system) can itself be an object of study for the mathematician. Each particular game may act as a coordinate system, illuminating key aspects of the subject. One can think about knots through the model of the diagrams. Other models (such as regarding the knots as specific kinds of embeddings in three dimensional space) are equally useful in other contexts. As we shall see, the diagrams are amazingly useful, allowing us to pivot from knots to other ideas and fields and then back to topology again.
The Reidemeister moves are illustrated in Figure 4.
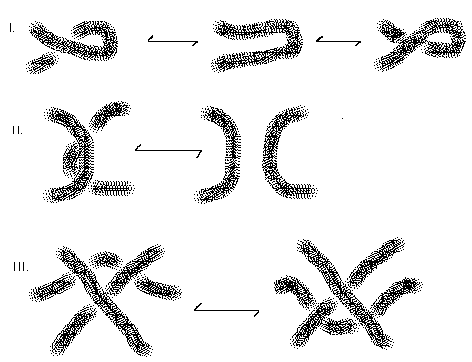
Figure 4 - Reidemeister Moves
The moves shown in Figure 4 are intended to indicate changes that are made in a larger diagram. These changes modify the diagram only locally as shown in the Figure. Figure 5 shows a sequence of Reidemeister moves from one diagram for a trefoil knot to another. In this illustration we have performed two instances of the second Reidemeister move in the first step, a combination of the second move and the third move in the second step and we have used "move zero" (a topological rearrangement that does not change any of the crossing patterns) in the last step. Move zero is as important as the other Reidemeister moves, but since it does not change any essential diagrammatic relationships it is left in the background of the discussion.

Figure 5
Knots as Analog Computers
We end this section with one more illustration. This time we take the bowline and close it into a loop. A deformation then reveals that the closed loop form of the bowline is topologically equivalent to two trefoils clasping one another, as shown in Figure 6.
This deformation was discovered by making a bowline in a length of rope, closing it into a loop and fooling about with the rope until the nice pair of clasped trefoils appeared. Note that there is more than one way to close the bowline into a loop. Figure 6 illustrates one choice. After discovering them, it took some time to find a clear pictorial pathway from the closed loop bowline to the clasped trefoils. The pictorial pathway shown in Figure 6 can be easily expanded to a full sequence of Reidemeister moves. In this way the model of the the knot in real rope is an analog computer that can help to find sequences of deformations that would otherwise be overlooked.
It is a curious reversal of roles that the original physical object of study becomes a computational aid for getting insight into the mathematics. Of course this is really a two way street. The very close fit between the mathematical model for knots and the topological properties of actual knotted rope is the key ingredient. Knots are analogous to integers. Just as we believe that objects follow the laws of arithmetic, we believe that the topological properties of knotted rope follow the laws of knot topology.

Figure 6
III. Invariants of Knots and Links - A First Pass
We want to be able to calculate numbers (or bits of algebra such as polynomials) from given link diagrams in such a way that these numbers do not change when the diagrams are changed by Reidemeister moves. Numbers or polynomials of this kind are called invariants of the knot or link represented by the diagram. If we produce such invariants, then we are finding topological information about the knot or link. The easiest example of such an invariant is the linking number of two curves, which measures how many times one curve winds around another. In order to calculate the linking number we orient the curves. This means that each curve is equipped with a directional arrow, and we keep track of the direction of the arrow when the curve is deformed by the Reidemeister moves. If the curves A and B are represented by an oriented link diagram with two components, attach a sign (+1 or -1) to each crossing as in Figure 7. Then the linking number, Lk(A,B), is the sum of these signs over all the crossings of A with B.

Figure 7
Of course, two singly linked rings receive linking number equal to +1 or
-1 as shown in Figure 8.
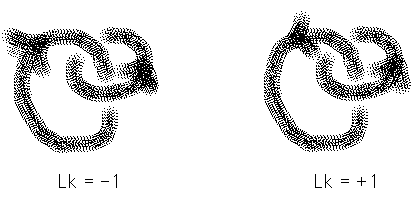
Figure 8
It can be shown that the linking number is invariant under the Reidemeister moves. That is, if we take a given diagram D (representing the curves A and B) and change it to a new diagram E by applying one of the Reidemeister moves, then the linking number calculation for D will be the same as the calculation for E. The calculation is unaffected by the first Reidemeister move because self-crossings of a single curve do not figure in the calculation of the linking number. The second Reidemeister move either creates or destroys two crossings of opposite sign, and the third move rearranges a configuration of crossing without changing their signs.
With these observations we have in fact proved that the singly linked rings are indeed linked! There is no possible sequence of Reidemeister moves from these rings to two separated rings because the linking number of separated rings is equal to zero, not to plus or minus one.
It may seem a minor accomplishment to prove something as obvious as the inseparability of this simple configuration, but it is the first step in the successful application of algebraic topology to the study of knots and links. The linking number has a long and interesting history, and there are a number of ways to define it, many considerably more complicated than the sum of diagrammatic signs. We shall discuss some of these alternative definitions at the end of this section.
One of the most fascinating aspects of the linking number is its limitations as an invariant. Figure 9 shows the Whitehead link, a link of two components with linking number equal to zero. The Whitehead link is indeed linked, but it requires methods more powerful than the linking number to demonstrate this fact.

Figure 9 - The Whitehead Link

Figure 10 - The Borromean Rings
These three rings are topologically inseparable, but if any one of them is ignored, then the other two are not linked.
Just in case these last few examples leave you pessimistic about the prospects of the linking number, here is a positive application. We shall use the linking number to show that the Möbius strip is not topologically equivalent to its mirror image. The Möbius strip is a circular band with a half twist in it as illustrated in Figure 11. The Möbius is a justly famous example of a surface with only one side and one edge. An observer walking along the surface goes through the half-twist and arrives back where she started only to discover that she is on the other local side of the band! It requires another trip around the band to return to the original local side. As a result there is only one side to the surface in the global sense. It is as though the opposite side of the world were infinitesimally close to us by drilling into the ground, but a full circumnavigation of the globe away by external travel.
To make matters even more surprising, there are actually two Mobius bands depending on the sense of the half twist. Call them M and M* as illustrated in Figure 11.
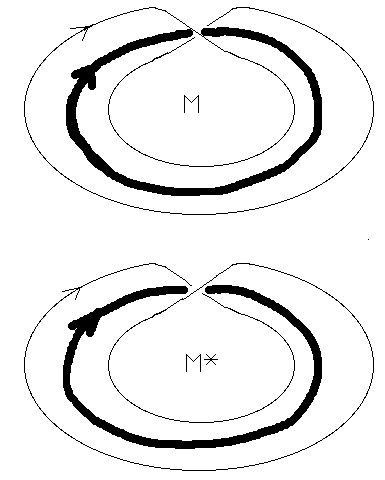
Figure 11 - Möbius and Mirror Möbius
If you make these two Möbius bands from strips of paper and try to deform one into the other without tearing the paper, you will fail (Try it!).
How can we understand the topological nature of the handedness of the Möbius band M? Draw a curve C down the center of the band M as shown in Figure 11. Compare this curve with the space curve formed by the boundary of the band. Orient these curves in parallel and compute the linking number. It is +1. The very same calculation for the mirror image band M* yields the linking number of -1.
If it were possible topologically to deform M to M* then the corresponding links (formed by the core curve and the boundary curve of the band) would be topologically equivalent, and hence they would have the same linking number. Since this is not the case, we conclude that M cannot be deformed to M*.
We have shown that there are two topologically distinct Möbius bands. The two bands are mirror images of one another in the sense that each looks like the image of the other in a reflecting mirror. When an object is topologically inequivalent to its mirror image, it is said to be chiral. We have demonstrated the chirality of the Möbius band.
Three Coloring a Knot
There is a remarkable proof that the trefoil knot is knotted. This proof goes as follows: Color the three arcs of the trefoil diagram with three distinct colors. Let’s say these colors are red, blue and purple. Note that in the standard trefoil diagram three distinct colors occur at each crossing.

Figure 12 - The Three Colored Trefoil
Now adopt the following coloring rule:
Either three colors or exactly one color occur at any crossing in the colored diagram.
Call a diagram colored if its arcs are colored and they satisfy this rule. Note that the standard unknot diagram is colored by simply assigning one color to its circle. A coloring does not necessarily have three colors on a given diagram. Call a diagram 3-colored if it is colored and three colors actually appear on the diagram.
Theorem. Every diagram that is obtained from the standard trefoil diagram by Reidemeister moves can be 3-colored. Hence the trefoil diagram represents a knot.

Figure 13 - Inheriting Coloring Under the Type Two Move

Figure 14 - Coloring Under Type Two and Three Moves
Rather than write a formal proof of this Theorem, we illustrate the coloring process in Figures 13 and 14. Each time a Reidemeister move is performed, it is possible to extend the coloring from the original diagram to the diagram that is obtained from the move. These extensions of colorings involve only local changes in the colorings of the original diagrams. The best way to see that this proof works is to do a few experiments yourself. The Figures 13 and 14 should get you started!
Note that in the case of the second move performed in the simplifying direction, although a color is lost in the arc that disappears under the move, this color must appear elsewhere in the diagram or else it is not possible for the two arcs in the move to have different colors (since there is a path along the knot from one local arc to the other). Thus 3-coloration is preserved under Reidemeister moves, whether they make the diagram simpler or more complicated. As a result, every diagram for the trefoil knot can be colored with three colors according to our rules. This proves that the trefoil is knotted, since an unknotted trefoil would have a simple circle among its diagrams, and the simple circle can be colored with only one color.
The Quandle and the Determinant of a Knot
There is a wide generalisation of this coloring argument. We shall replace the colors by arbitrary labels for the arcs in the diagram and replace the coloring rule by a method for combining these labels. It turns out that a good way to articulate such a rule of combination is to make the label on one of the undercrossing arcs at a crossing a product (in the sense of this new mode of combination) of the labels of the other two arcs. In fact, we shall assume that this product operation depends upon the orientation of the arcs as shown in Figure 15.
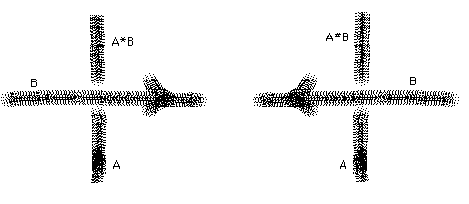
Figure 15 - The Quandle Operation
In Figure 15 we show how a label a on an undercrossing arc combines with a label b on an overcrossing arc to form c=a*b or c=a#b depending upon whether the overcrossing arc is oriented to the left or to the right for an observer facing the overcrossing line and standing on the arc labelled a.
This operation depends upon the orientation of the line labelled b so that a*b corresponds to b pointing to the right for an observer approaching the crossing along a, and a#b corresponds to b pointing to the left for the same observer. All of this is illustrated in Figure 15.
The binary operations * and # are not necessarily associative. For example, our original color assignments of R (red), B (blue) and P (purple) for the trefoil knot correspond to products R*R=R, B*B=B, P*P=P, R*B=P, B*P=R, P*R=B. Then R*(B*P) = R*R=R while (R*B)*P = P*P = P.
We shall insist that these operations satisfy a number of identities so that the labelling is compatible with the Reidemeister moves.
In Figure 16 I have illustrated the diagrammatic justification for the following algebraic rules about * and #. An algebraic system satisfying these rules is called a quandle [JOY].
1. a*a = a and a#a = a for any label a.
2. (a*b)#b = a and (a#b)*b = a for any labels a and b.
3. (a*b)*c = (a*c)*(b*c) and (a#b)#c = (a#c)#(b#c) for any labels a,b,c.
These rules correspond, respectively to the Reidemeister moves 1,2 and 3.
Labellings that obey these rules can be handled just like the 3-coloring that we have already studied. In particular a given labelling of a knot diagram means that it is possible to label (satisfying the rules given above for the labels) any diagram that is related to it by a sequence of Reidemeister moves. However, not all the labels will necessarily appear on every related diagram, and for a given coloring scheme and a given knot, certain special restrictions can arise.
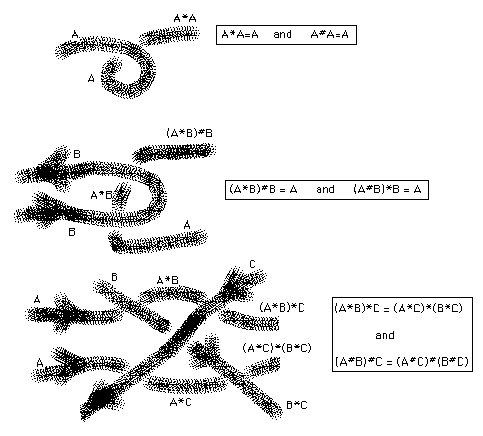
Figure 16 - Quandle Identities
To illustrate this, consider the color rule for numbers: a*b = a#b = 2b-a.
This satisfies the axioms as is easy to see. Figure 17 shows how, on the trefoil, such a coloring must obey the equations
a*b=c, c*a=b,b*c=a. Hence 2b-a=c, 2a-c=b, 2c-b = a. For example, if a=0 and b=1, then c=2b-a = 2 and a = 2c-b = 4-1 = 3. We need 3=0. Hence this system of equations will be satisfied for appropriate labellings in Z/3Z, the integers modulo three, a modular number system.
For the reader unfamiliar with the concept of modular number system, consider a standard clock whose dial is labelled with the hours 1,2,3,..., 11,12. We ask what time is it 4 hours past the hour of 10? The answer is 2, and one can say that in the arithmetic of this clock 10+4=2. In fact 12=0 in this arithmetic because adding 12 hours to the time does not change the time indicated on the clock. We work in clock arithmetic by remembering to set blocks of 12 hours to zero. One can multiply in this arithmetic as well. The square of the present time is 1 o’clock, what time is it? The answer is 7 since 7 squared is 49 and 49 is equal to 1 on the clock.
We say that the clock represents a modular number system Z/12Z with modulus 12. It is convenient in mathematics to think of the elements of Z/12Z as the set {0,1,2,...,11}. Since 0=12 this takes care of all the hours.
In general we can consider Z/nZ where n is any positive integer modulus.
The resulting modular number system has elements {0,1,2,...,n-1} and is handled just as though there were a clock with n hours rather than 12.
In such a system one says that x = y (mod n) if the difference between x and y is divisible by n. For example 49 =1 (mod 12) since 49-1=48 is divisible by 12.
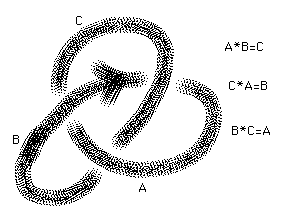
Figure 17 - Equations for the Trefoil Knot
The modular number system, Z/3Z, reproduces exactly the three coloring of the trefoil, and we see that the number 3 emerges as a characteristic of the equations associated with the knot. In fact, 3 is the value of a determinant that is associated with these equations, and its absolute value is an invariant of the knot. For more about this construction, see [K10, Part 1, Chapter 13].
Here is another example: For the figure eight knot E, we have that
the modulus is 5. This shows that E is indeed knotted and that it is distinct from the trefoil. We can color (label) the figure eight knot with five "colors" 0,1,2,3,4 with the rules: a*b = 2b-a (mod 5). See Figure 18.
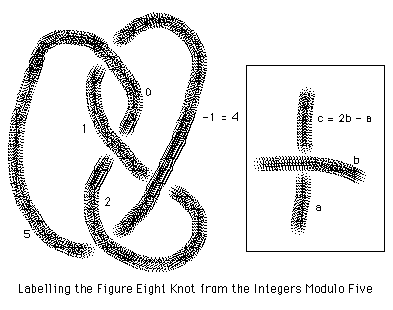
Figure 18 - Five Colors for the Figure Eight Knot
Note that in coloring the figure eight knot we have only used four out of the five available "colors" from the set {0,1,2,3,4}. Figure 18 uses the colors 0,1,2 and 4. In [KH] we define the coloring number of a knot or link K to be the least number of colors (greater than 1) needed to color it in the 2b-a fashion for any diagram of K. It is a nice exercise to verify that the coloring number of the figure eight knot is indeed four. In general the coloring number of knot or link is not easy to determine. This is an example of a topological invariant that has subtle combinatorial properties.
Other knots and links that we have mentioned in this section can be shown to be knotted and linked by the modular method. The reader should try it for the Borommean rings and the Whitehead link.
The coloring (labelling) rules as we have formalised them can be described as axioms for an algebra associated with the knot. This is called the quandle [JOY]. It has been generalised to the crystal [K10], the interlock algebra [K15], and the rack [FR]. The quandle is itself a generalisation of the fundamental group of the knot complement [CF].
The Alexander Polynomial
The modular labelling method has a marvellous generalisation to the Alexander polynomial of the knot. This comes about through generalised coloring rules a*b =ta + (1-t)b and a#b=t-1a + (1-t-1)b, where t is an indeterminate. It is a nice exercise to verify that these rules satisfy the axioms for the quandle. This algebraic structure is called the Alexander Module.
The case t=-1 gives the rule 2b-a that we have already considered. By coloring diagrams with arbitrary t, we obtain a polynomial that generalises the modulus. This polynomial is the Alexander polynomial.
Alexander [AL] described it differently in his original paper, and there is a remarkable history to the development of this invariant. See [CF],[FOX],[CON],[K1],[K2],[K4] for more information. The flavor of this relationship can be seen by doing a little experiment in labelling the trefoil diagram shown in Figure 19. The circularity inherent in the knot diagram results in relations that must be satisfied by the module action. In Figure 19 we see directly by labelling the diagram that if arc 1 is labelled 0 and arc 2 is labelled a, then
(t + (1-t)2)a=0. In fact, t + (1-t)2 = t2 -t +1 is the Alexander polynomial of the trefoil knot. The Alexander polynomial is an algebraic modulus for the knot.
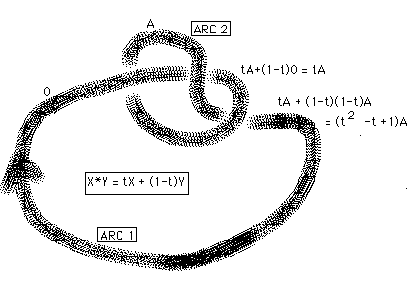
Figure 19 - Alexander Polynomial of the Trefoil Knot
IV. The Jones Polynomial
Our next topic describes an invariant of knots and links of quite a different character than the modulus or the Alexander polynomial of the knot. It is a "polynomial" invariant of knots and links discovered by Vaughan Jones in 1984 [JO2]. Jones’ invariant, usually denoted VK(t), is a polynomial in the variable t1/2 and its inverse t-1/2. One says that VK(t) is a Laurent polynomial in t1/2. Superficially, the Jones polynomial appears to be just another polynomial invariant of knots and links, somewhat similar to the Alexander polynomial. When I say that the Jones polynomial is of a different character, I mean something deeper, and it will take a little while to explain this difference. A little history will help.
The Alexander polynomial was discovered in the 1920’s and until 1984 no one had found another polynomial invariant of knots and links that was not a simple generalisaton of the Alexander polynomial. Vaughan Jones discovered a new polynomial invariant of knots and links that had some very remarkable properties. The Alexander polynomial cannot detect the difference between any knot and its mirror image. What made the Jones polynomial such an exciting discovery for knot theorists was the fact that it could detect the difference between many knots and their mirror images. Later other properties began to emerge. It became a key tool in proving properties of alternating links (and generalisations) that had been conjectured since the last century [K3],[MUR1],[MUR2],[TH],[MT].
It turns out the the Jones polynomial is intimately related to a number of topics in mathematical physics. Curiously, it is actually easier to define and verify the properties of the Jones polynomial than for any other invariant in the theory of knots (except of course the linking number). We shall devote this section to the defining properties of the Jones polynomial, and later sections to the relationships with physics.
Here are a set of axioms for the Jones polynomial. The polynomial was not discovered in the form of these axioms. The axioms are in a format analogous to the framework that John H. Conway [CON],[K1],[K2], discovered for the Alexander polynomial. I am starting with these axioms because they give a quick access to the polynomial and to sample computations.
Axioms for the Jones Polynomial
1. If two oriented links K and K’ are ambient isotopic, then
VK(t)= VK’(t).
2. If U is an unknotted loop, then VU(t) = 1.
3. If K+, K-, and K0 are three links with diagrams that differ only as shown in the neighborhood of a single crossing site for K+ and K- (see Figure 20), then t-1 VK+(t) - tVK-(t) = (t1/2 - t-1/2)VK0(t).
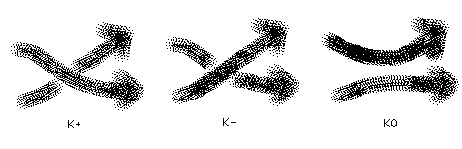
Figure 20
The axioms for VK(t) are a consequence of Jones’ original definition of his invariant. He was led to this invariant by a trail that began with the study of von Neumann algebras [JO1] (a branch of algebra directly related to quantum theory and to statistical mechanics) and ended in braids, knots and links. The Jones polynomial has a distinctly different flavor from the Conway-Alexander polynomial even though it can be axiomatised in a very similar way. In fact, this similarity of axiomatics points to a common generalisation (the Homfly(Pt) polynomial) [F],[PT] and to another generalisation (the Kauffman polynomial) [K9], and then to further generalisations in the connection with statistical mechanics [K8],[JO5],[AW].
To this date no one has found a knotted loop that the Jones polynomial does not declare to be knotted. Thus one can make the
Conjecture: If a single component loop K is knotted, then VK(t) is not equal to one.

Figure 21
While it is possible that the Jones polynomial is able to detect the property of being knotted, it is not a complete classifier for knots. There are inequivalent pairs of knots that have the same Jones polynomial. Such a pair is shown in Figure 21. These two knots, the Kinoshita-Terasaka knot and the Conway knot, both have the same Jones polynomial but are different topologically. Incidentally these two knots are examples whose knottedness cannot be detected by the Alexander polynomial.
Lets get to work and use the axioms to compute the Jones polynomial for the trefoil knot. To this end, there is a useful device called the skein tree. A skein tree is obtained from a given knot or link diagram by recording the knots and links obtained from this diagram by smoothing or switching crossings. Each node of the tree is a knot or link. The nodes farthest from the original knot or link are unknotted or unlinked. Such a tree can be produced from a given knot or link by using the fact that any knot or link diagram can be transformed into an unknotted (unlinked) diagram by a sequence of crossing switches. See Figure 22.
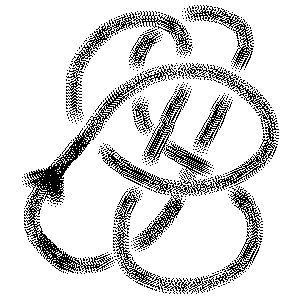
Figure 22 - A Standard Unknot
In Figure 22 I have illustrated a "standard unknot diagram". This diagram is drawn by starting at the arrowhead in the Figure and tracing the diagram in such a way that one always draws an over crossing before drawing an undercrossing. This is the easiest possible knot diagram to draw since one never has to make any corrections - just pass under when you want to cross an an already created line in the diagram. Standard unknot diagrams are always unknotted. Try your hand at the one in Figure 22 and you will see why this is so.
Using the fact that standard unknot diagrams are available, we can use the difference between a given diagram K and a standard unknot with the same plane projection to give a procedure for switching crossings to unknot the diagram K. This switching procedure can be used to produce a skein tree for calculating the Jones polynomial of K.
We have illustrated in Figure 23 a skein tree for the computation of the Jones polynomial of the trefoil knot. The tree reduces the calculation of the Jones polynomial of the trefoil diagram to the calculation of certain unknots and unlinks. In order to see how to calculate an unlink it is useful to observe the behaviour of the axioms in this case:
t-1 VU+ - tVU- = (t1/2 - t-1/2)VU0.
Here U+ and U- denote unknots with single positive and negative twists in them. U0, obtained by smoothing the crossing of U+ or U-, is an unlinked pair of circles with no twists. See Figure 24.

Figure 23
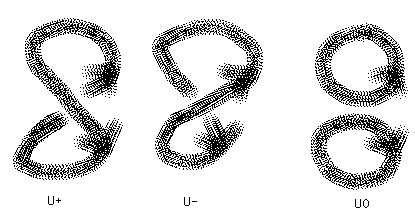
Figure 24
Therefore ( t-1- t)1 = (t1/2 - t-1/2)VU0.
Hence d= VU0 =( t-1- t)/(t1/2 - t-1/2) = -(t1/2 + t-1/2).
Thus we see that an extra unknotted component of the link multiplies the invariant by d=-(t1/2 + t-1/2). Here T denotes the trefoil knot, U denotes the unknot and L denotes the link of two unknotted circles as shown in Figure 23. With this fact in place, we find that
t-1 VT - tVU = (t1/2 - t-1/2)VL
t-1VL - td = (t1/2 - t-1/2)VU
Thus VL = t( td + (t1/2 - t-1/2)) = -t5/2 - t1/2.
Hence VT = t(t + (t1/2 - t-1/2)VL) = t(t + (t1/2 - t-1/2)(-t5/2 - t1/2))
= t(t -t3-t+t2+1) = t(-t3+t2+1) = -t4+t3+t.
The same calculation applied to the mirror image T* (obtained by reversing all the crossings of T) of the trefoil yields the invariant
VT* = -t-4+t-3+t-1. This shows how the Jones polynomial discriminates between the trefoil and its mirror image, thereby proving that there is no ambient isotopy from T to T*.
This method of calculating the Jones polynomial from its axioms does not tell us why the invariant works. It is possible to analyse this method of calculation and show that it does not depend upon the choices that one makes in the process and that it gives topological information about the knot or link in question. There is a different way to proceed that leads to a very nice formula for the Jones polynomial as a sum over "states" of the diagram. In this formulation, the polynomial is well defined from the beginning, and we can see the topological invariance arise in the course of adjusting certain parameters of a well-defined function. Our next topic is this state summation model for the Jones polynomial.
V. The Bracket State Sum
In the last section we gave axioms for the Jones polynomial and showed how to compute it by skein calculations from these axioms. In this section we shall show one way to prove that the Jones polynomial is well-defined by these axioms, and that it is an invariant of ambient isotopy of links in three dimensional space. In order to accomplish this aim, we shall give a different definition of the polynomial as a certain summation over combinatorial configurations associated with the given link diagram. This summation will be called a state summation model for the Jones polynomial.
In fact, we shall first construct a state summation called the bracket polynomial [K3], and then explain how to modify the bracket polynomial to obtain the Jones polynomial. The bracket polynomial has a rather natural development, and is defined for unoriented link diagrams.
We work with diagrams for unoriented knots and links. To each crossing in the diagram assign two local states with labels A and B, as shown in Figure 25.
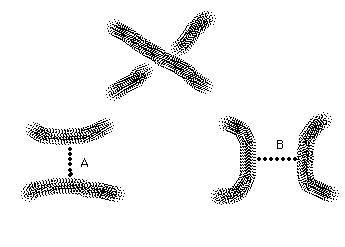
Figure 25
(In the A-state the regions swept out by a counterclockwise turn of the overcrossing line are joined. In the B-state the regions swept out by a clockwise turn of the overcrossing line are joined.)
A state S of a diagram K consists in a choice of local state for each crossing of K. Thus a diagram with N crossings will have 2N states. Two states S and S' of the trefoil diagram are indicated in Figure 26.

Figure 26
States are evaluated in two ways. These ways are denoted by <K|S> and by ||S||. The norm of the state S, ||S||, is defined to be one less than the number of closed curves in the plane described by S. In the example in Figure 26, we have ||S||=1 and ||S'||=0. The evaluation <K|S> is defined to be the product of all the state labels (A and B) in the state. Thus in Figure 26 we have <K|S>=A3 and <K|S'>=A2B.
Taking variables A,B and d, we define the state summation associated to a given diagram K by the formula
<K> = S <K|S>d||S||.
In other words, for each state we take the product of the labels for that state multiplied by d raised to the number of loops in the state. <K> is the summation of this state evaluation over all the states in the diagram for K.
(The notation S means "sum over all instances of S".) We will show that the state summation <K> is invariant under the second and third Reidemeister moves if we take B = 1/A and d=-(A2 +B2). A normalisation then enables us to obtain invariance under all three Reidemeister moves, and hence topological information about knots and links. (See [K3] for more information about the bracket and its relationship with the Jones polynomial.) There is a great deal of topological information in the calculations that ensue from the bracket polynomial. In particular, one can distinguish many knots from their mirror images, and it is possible that the bracket calculation can detect whether a given diagram is actually knotted.
First Steps in Bracketology
The first constructions related to the bracket polynomial are quite elementary. There are two basic formulas that are reminiscent of the exchange relations we have already seen for the Jones polynomial. These formulas are as shown in Figure 27.
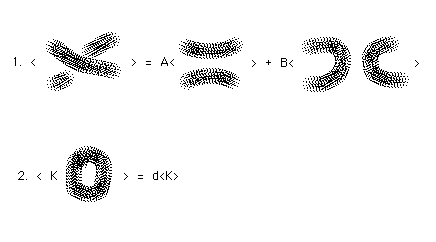
Figure 27 - Bracket Equations
Here the small diagrams indicate parts of larger diagrams that are otherwise identical.
Formula 1. just says that the state summation breaks up into two sums with respect to a given crossing in the diagram. In one sum, we have made a smooothing of type A at the crossing, while in the other sum we have made a smoothing of type B. The factors of A and B indicated in the formula are the contributions to the product of vertex weights from this crossing. All the rest of the two partial sums can be interpreted as bracket evaluations of the smoothed diagrams.
Formula 2. just states that an extra simple closed curve in a diagram multiplies its bracket evaluation by the loop value d. Note that a single loop receives the value 1.
With the help of these two formulas, we can compute some basic bracket evaluations. Note that we have not yet specialised the variables A,B and d. We shall analyse just what specialisation will produce an invariant of knots and links. The advantage to having set up the definition of the bracket polynomial in this way is exactly that we have a method of labelling link diagrams with algebra, and it is possible to then adjust the evaluation so that it is invariant under Reidemeister moves. To this end, the next Lemma tells us how the general bracket behaves under a Reidemeister move of type two. Essential diagrams for this Lemma are in Figure 28.
Lemma. Let K be a given link diagram, and let K’ denote a diagram that is obtained from K by performing a type 2 Reidemeister move in the simplifying direction (eliminating two crossings from K). Let K’’ be the diagram obtained from K by replacing the site of the type two move by two arcs in the opposite pattern to the form of the simplified site in K’. (The diagrams in Figure 28 illustrate this construction.) Then
<K> = AB<K’> + (ABd + A2 + B2)<K’’>.
Proof. Consider the four local state configurations that are obtained from the diagram K on the left hand side of the equation, as illustrated in Figure 28. The formula follows from the fact that one of these states has coefficient AB and the other three have the same underlying diagram and respective coefficients ABd (after converting the loop to a value d), A2 and B2. This completes the proof of the Lemma.//
With the help of this Lemma it is now obvious that if we choose B=1/A and d + A2 + B2 = 0, then <K> is invariant under the second Reidemeister move.
Once this choice is made, the resulting specialised bracket is invariant under the third Reidemeister move, as illustrated in Figure 29.

Figure 28 - Type Two Changes
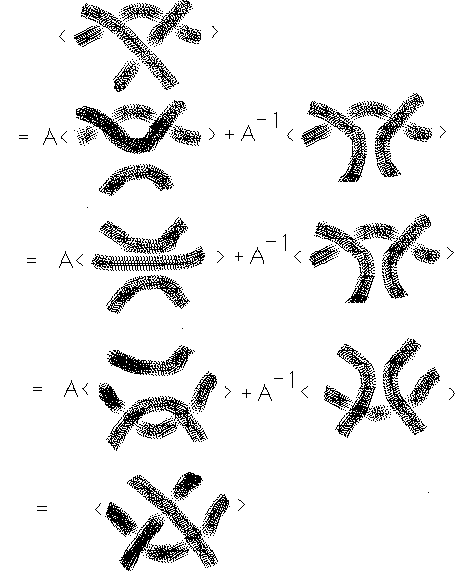
Figure 29 - Type III Invariance of the Bracket
Finally, we can investigate bracket behaviour under the first Reidemeister move.
Lemma. Let <K> denote the bracket state sum with B=A-1 and
d=-A2-A-2. Then <K> is invariant under the Reidemeister moves II and III and on move I behaves as shown below.
< K(+) > = (-A3)< K >
< K(-) > = (-A-3)< K >.
Here K(+) denotes a diagram with a simplifying move of type I available where the crossing that is to be removed has type +1. K is the diagram obtained from K(+) by doing the type I move. Similarly, K(-) denotes a diagram with a simplifying move of type I available where the crossing that is to be removed has type -1. Figure 30 illustrates the diagrams for K(+) and K(-).
Proof. See Figure 30 for the behaviour under type I moves.
We have already verified the other statements in this Lemma.//
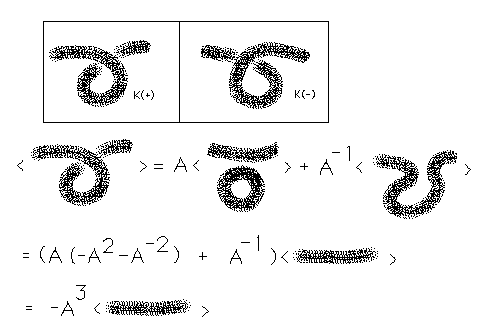
Figure 30 - Bracket under Type I Move
Framing Philosophy - Twist and Writhe
Is it unfortunate that the bracket is not invariant under the first Reidemeister move? No, it is fortunate! First of all, the matter is easy to fix by a little adjustment: Let K be an oriented knot or link, and define the writhe of K, denoted w(K), to be the sum of the signs of all the crossings in K. Thus the writhe of the right-handed trefoil knot is three.
The writhe has the following behaviour under Reidemeister moves:
(i) w(K) is invariant under the second and third Reidemeister moves.
(ii)w(K) changes by plus or minus one under the first Reidemeister move:
w( K(+) ) = w(K) +1
w(K(-)) = w(K) -1.
(Here we use the notation of the previous Lemma as shown in Figure 30.)
Thus the writhe behaves in a parallel way to the bracket on the type I moves, and we can combine writhe and bracket to make a new calculation that is invariant under all three Reidemeister moves. We call the fully invariant calculation the "f-polynomial" and define it by the equation
fK(A) = (-A3)-w(K)<K>(A).
Up to this normalisation, the bracket gives a model for the original Jones polynomial. The precise relationship is that
VK(t) = fK(t-1/4) where w(K) is the sum of the crossing signs of the oriented link K, and <K> is the bracket polynomial obtained by ignoring the orientation of K.
We shall return to this relationship with the Jones polynomial in a moment, but first a little extra mathematical philosophy: Another way to view the fact of the bracket’s lack of invariance under the first Reidemeister move is to see that the bracket is an invariant of knotted and linked bands embedded in three dimensional space. Regard a link diagram as shorthand for an embedding of bands as shown in Figure 31.

Figure 31 - Bands and Twists
In Figure 31 we have illustrated a link diagram ;for the trefoil knot in a thick dark mode of drawing. This diagram is juxtaposed with a drawing of a knotted band that parallels that knot diagram . The band has two boundary components that proceed (mostly in the plane) parallel to one another. The curl in the knot diagram becomes a flat curl in the band that is ambient isotopic to a full twist ( two half twists) in the band. This isotopy is indicated in Figure 31. The top of Figure 31 shows a full twist in a band and two flat curls that both give rise to this same full twist by ambient isotopy that leaves their ends fixed. Each component of a link diagram is replaced by a parallelled version - the analog of a ribbbon-like strip of paper attached to itself with an even number of half-twists. The first Reidemeister move no longer applies to this shorthand since we can, at best, replace a curl by a twist as shown in Figure 31.
In fact, as Figure 31 shows, there are two distinct curls corresponding to a single full twist of a band. The bracket (and the writhe) behave the same way on both of these twists. This means that we can re-interpret the bracket as an invariant of the topological embeddings of knotted, linked and twisted bands in three-dimensional space. This means that the bracket has a fully three-dimensional interpretation, although its definition depends upon the use of planar projections.
Calculating the Bracket
In Figure 32 we show a tree for calculating the bracket polynomial of the trefoil knot T.
It follows at once from the behaviour of the bracket on curls that the contributions of the three (farthest from the trefoil itself) branches of this tree add to give the bracket polynomial of the trefoil:
<T> = A2(-A3) + AA-1(-A-3) + A-1(-A-3)2 = -A5 -A-3+A-7.
Hence
fT = (-A3)-w(T)<T> = A-4 + A-12 - A-16.
Note that we managed only three branches in the tree for this calculation rather than the full expansion into the eight states. A savings like this is always possible, because we know how the bracket behaves on curls. The resulting expansion gives a sum of monomials and is useful for thinking about the properties of the invariant.

Figure 32 - Tree for Bracket of Trefoil
Mirror Mirror
The knot K* obtained by reversing all the crossings of K is called the mirror image of K. K* is the mirror image of the knot that would ensue if the plane on which the knot is drawn were a mirror. It is easy to see that <K*>(A) = <K>(A-1) and that fK*(A) = fK(A-1). Thus, if K is ambient isotopic to K* (all three Reidemeister moves allowed), then
fK(A) = fK*(A) = fK(A-1).
Returning to the evaluation of the f-invariant for the trefoil, note that
fT(A-1) is not equal to fT(A). Therefore, the trefoil knot T and its mirror image T* are topologically distinct. The proof that we have given for it is the simplest proof known to this author. Note that we have given a complete proof of this fact, starting with the Reidemeister moves, constructing and applying the bracket invariant.
A knot is said to be chiral if it is not ambient isotopic to its mirror image.
The words chiral and chirality come from physical chemistry and natural science. A knot that is equivalent to its mirror image is said to be achiral.
(Or amphicheiral in the speech of knot theorists). Many knots are achiral. The reader may enjoy verifying that the figure eight knot shown in Figure 33 is ambient isotopic to its mirror image.
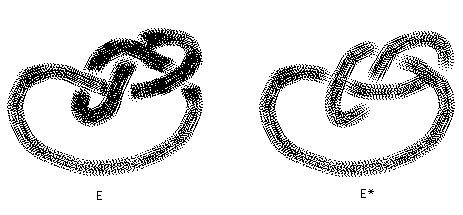
Figure 33 - Figure Eight Knot and its Mirror Image
A complete understanding of the problem of determining whether a knot is chiral remains in the far distance. The new invariants of knots and links have enhanced our understanding of this difficult question.
Return to the Jones Polynomial
Now lets verify that the bracket does indeed give a model for the Jones polynomial. To see this, consider fK(A) = (-A3)-w(K)<K>(A).
Since the writhe, w(K), is obtained by summing signs over all the crossings of K, we can interpret the factor (-A3)-w(K) as
the product of contributions of (-A3) or (-A3)-1 one from each crossing and depending upon the sign of the crossing. Thus we can write an oriented state expansion formula for fK as shown below where K+ and K- denote links with corresponding sites with oriented crossings, K0 is the result of smoothing the crossing in an oriented fashion and K& is the result of smoothing the crossing against the orientation.
f K+ = (-A3)-1Af K0 + (-A3)-1A-1f K& .
Hence,
f K+ = -A-2fK0 -A-4fK&
and similarly, for a negative crossing
f K- = -A2fK0 -A4fK&
Letting VK(t) = fK(t-1/4) we have
VK+ = -t1/2VK0 - tVK&
and
VK- =-t-1/2VK0 -t-1VK&
Therefore,
t-1VK+ -tVK- = (t1/2 - t-1/2)VK0
We leave the rest of the verification that VK(t) is the Jones polynomial (see section 4) to the reader (You should check that it has the right behaviour on unknotted loops.).
VI. Vassiliev Invariants
We have seen how it is fundamental to take the difference of an invariant at a positive crossing and at a negative crossing, leaving the rest of the diagram alone. The earliest instance of this is the Conway polynomial [CON], CK(z) with its exchange identity
C K+ - C K- = z CK0
Vassiliev [V] gave new meaning to this sort of identity by thinking of the structure of the entire space of all mappings of a circle into three dimensional space. This space of mappings includes mappings with singularities where two points on a curve touch. He interpreted the equation
ZK+ - ZK- = ZK#
as describing the difference of values across a singular embedding K# where K# has a transverse singularity in the knot space as illustrated in Figure 34. (In a transverse singularity the curve touches itself along two different directions.)
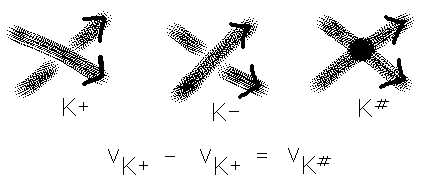
Figure 34 - Difference Equation
The Vassiliev formula serves to define the value of the invariant on a singular embedding in terms of the the values on two knots "on either side" on this embedding. This Vassiliev formula serves to describe a method of extending a given invariant of knots to a corresponding invariant of embedded graphs with controlled singularities of this transverse type. This idea had been considered before Vassiliev. Vassiliev carried out his program of analysing the singular knot space using techniques of algebraic topology, and in the course of this investigation he discovered a key concept that had been completely overlooked in the context of graph invariants. That concept is the idea of an invariant of finite type.
Definition. We shall say that ZG is an invariant of finite type i if ZG vanishes for all graphs with greater than i nodes.
This concept was extracted from Vassiliev’s work by Birman and Lin [BIL]. A (rigid vertex) invariant of knotted graphs is a Vassiliev invariant of finite type i if it satisfies the identity
ZK+ - ZK- = ZK#
and it is of finite type i. In rigid vertex isotopy the cyclic order at the vertex is preserved, so that the vertex behaves like a rigid disk with flexible strings attached to it at specific points.
Vassiliev invariants form an extraordinary class of knot invariants.
It is an open problem whether the Vassiliev invariants are sufficient to distinguish knots that are topologically distinct.
Vassiliev began an analysis of the combinatorial conditions on graph evaluations that could support such invariants. The key observation is the
Lemma. If ZG is a Vassiliev invariant of finite type i, then ZG is independent of the embedding of the graph G when G has i vertices.
Proof. Suppose that G is an embedded graph G with i nodes.
If we switch a crossing in G to form G’ then the exchange relation for the Vassiliev invariant says that ZG - ZG’ = ZG’’ where G’’ has one more node than G or G’. But then G’’ has i+1 nodes and hence ZG’’ = 0. Therefore
ZG = ZG’. This shows that we can switch crossings in any embedding of G without changing the value of ZG. It follows from this that ZG is independent of the embedding and depends only on the graph G. This completes the proof of the Lemma. //
For a Vassiliev invariant of type i, there is important information in the values it takes on graphs with exactly i nodes. These evaluations do not depend upon the embedding type of the graph. However, not just any such graphical evaluation will extend to give a topological invariant of knots and graphs. There are necessary conditions. Vassiliev found a version of these conditions through his analysis of the knot space and Ted Stanford [ST] , a student of Joan Birman, discovered the beautiful topological meaning of these conditions in relation to the switching identity. Stanford’s argument goes as follows: Consider a singular crossing that has an arc from the diagram passing underneath it as shown in Figure 35.

Figure 35 - Embedded Four Term Relation
Four crossing switches will take that arc above the singular crossing and return the diagram to a position that is topologically equivalent to its original position.
Each crossing switch gives an equation. There are four equations. Add them up and you get an identity among the values of the invariant on four diagrams. Call this the four-term relation. This identity is illustrated in the second box in Figure 35.
Now recall from the Lemma we proved above that for a Vassiliev invariant of type i, the graphs with i nodes have values that are independent of their embeddings in three dimensional space. This means that at the top level
(The i noded graphs for a Vassiliev invariant of type i will be called the top level.) the four term relations will be relations among the evaluations of abstract graphs. At the top level the four term relations will be purely combinatorial conditions related to the topology.
How shall we think of abstract 4-valent graphs corresponding to singular embeddings of a knot? An abstract knot is just a circle. An abstract singular knot is a circle with pairs of points marked that become the singular points in the embedding. Indicate these paired points by arcs between them. Call the resulting structure a chord diagram. See the example at the beginning of Figure 36.
In the language of the chord diagrams the 4-term relation at the top level (see the discussion of the top level in the paragraph above) becomes the equation shown in Figure 36. This can be seen by translating the relation in Figure 35 into the language of chord diagrams. In Figure 36 we have indicated parts of the chord diagram that are neighbors by showing an outer bracket connecting them. Those sites that are neighbors can have no other chords between them. Otherwise there can be many chords in these diagrams that are not indicated, just so long as the diagrams in the equation for the four-term relation differ only as shown in the Figure.
If you can write down a top level evaluation of chord diagrams that satisfies the 4-term relation, then you have the raw data for a Vassiliev invariant. Sucn an evaluation of chord diagrams is called a weight system for a Vassiliev invariant. By the Theorems of Kontsevich and Bar-Natan [BAR95], this raw data guarantees the existence of at least one invariant that satisfies the top level evaluation.
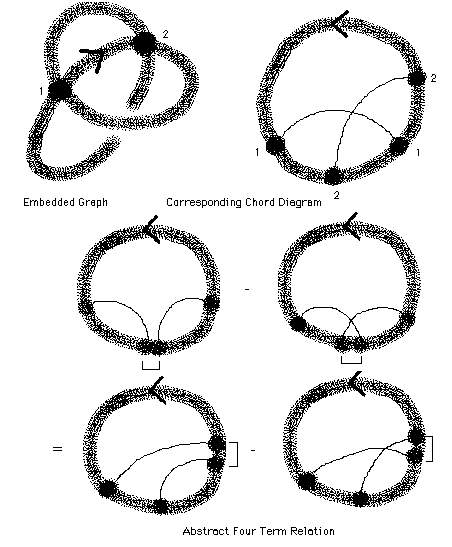
Figure 36 - Abstract Four Term Relation Via Chord Diagrams
The world is rife with Vassiliev invariants. Birman and Lin [BIL] showed directly that the Jones polynomial and its generalisations give rise to Vassiliev invariants. In the case of the Jones polynomial here is an easy proof of their result:
Theorem. Let VG(t) denote the Jones polynomial extended to rigid
vertex 4-valent graphs by the formula VK+ - VK- = VK# .
Let vi(G) denote the coefficient of xi in the expansion of VG(exp(x)). Then vi(G) is a Vassiliev invariant of type i.
Proof. Use the identities from the end of section 5.
VK+ = -t1/2VK0 - tVK&
VK- =-t-1/2VK0 -t-1VK&.
Substitute t =exp(x).
It follows at once that VK# = VK+ - VK- is divisible by x.
Hence VG is divisible by xi when G has i nodes. This implies that the coefficients vi(G)=0 if G has more than i nodes. Hence the coefficients vi(G) are of finite type, proving the Theorem.//
With the help of theorems of this type it is possible to study Vassiliev invariants by studying the structure of known invariants of knots and links. In particular it is possible to justify the structure of many weight systems in terms of known invariants. We shall not go into these sorts of investigations in this exposition. The next section shows how the algebraic study of Lie algebras is directly related to the construction of Vassiliev invariants. This is one beginning of a whole world of relationships between knot theory and algebra.
VII. Vassiliev Invariants and Lie Algebras
The subject of Lie algebras is an algebraic study with a remarkable connection with the topology of knots and links. The purpose of this section is to first give a brief introduction to the concept of a Lie algebra and then to show the deep connection between these algebras and the structure of Vassiliev invariants for knots and links, as described in the previous section.
In order to understand the idea behind a Lie algebra it is helpful to first consider the concept of a group. A set G is said to be a group if it has a single binary operation * such that
1. Given a and b in G then a*b is also in G.
2. If a,b,c are in G then (a*b)*c = a*(b*c).
3. There is an element E in G such that E*a = a*E = a for all a in G.
4. Given a in G there exists an element a-1 in G such that a*a-1 = a-1*a=E.
One of the most fertile sources of groups is matrix algebra. Recall that an
n x n matrix A is an array of numbers Aij (real or complex), A=(Aij), where i and j range in value from 1 to n. One defines the product of two matrices by the formula (AB)ij = Žk AikBkj where k runs from 1 to n in this summation.
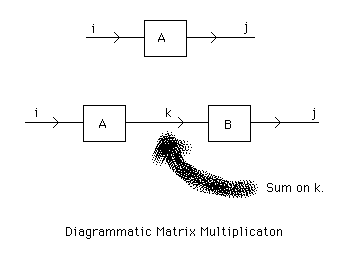
Figure 37
Many facts about matrices become quite transparent in this notation. For example, the trace of A, denoted tr(A), is the sum of the diagonal entries Aii where i ranges from one to n. The diagrammatic proof of the basic formula tr(AB) = tr(BA) is illustrated in Figure 38.
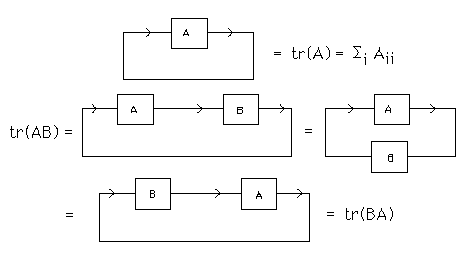
Figure 38
For a given value of n, we let Mn(R) denote the set of all n x n matrices with coefficients in the real numbers R. We let A*B = AB denote the product of matrices and we let E denote the matrix whose entries are given by the formula: Eii=1 for all i, and Eij=0 if i is not equal
to j. With this choice of multiplication and identity element E, Mn(R) satisfies the first three axioms for a group. However there are matrices A that have no inverse (A-1 so that AA-1 = E). For example the matrix 0, all of whose entries are zero, is a matrix without an inverse. Thus Mn(R) is not itself a group.
There is a criterion for a matrix to have an inverse. This is simply that the determinant, Det(A), should be non-zero. Thus the largest group of matrices of size n x n that we can devise is the set of all matrices A such that Det(A) is non-zero. This is called the general linear group and is denoted by GLn(R). There are many interesting subgroups of this large group of matrices. One example is the group Sl(n) of all matrices with determinant equal to one. We may also restrict to orthogonal matrices A over R. These are invertible matrices A such that At = A-1 where At denotes the transpose of the matrix A: Atij = Aji. The group of orthogonal matrices is denoted by O(n).
The intersection of O(n) and Sl(n) is denoted SO(n). SO(n) consists in the orthogonal matrices of determinant equal to one. In the case n=2, SO(2) consists in rotations of the plane that fix the origin, and in the case of n=3, SO(3) consists in rotations of three dimensional space about specified axes.
SO(3) has a fascinating collection of finite subgroups including the symmetries of the classical regular solids: the tetrahedron, the cube, the octahedron, the dodecahedron and the icosahedron. Ultimately, the matrix groups become a language for the precise expression of symmetry.
We now ask when a matrix A can be written in the form
A = eB= E + (1/1!)B + (1/2!)B2 + (1/3!)B3 + ...
for some other matrix B. Since eB = limit (E+B/m)m where the limit is taken as m approaches infinity, we can regard (E+B/m), for m large, as an "infinitesimal" version of the matrix A, and one refers to B as an "infinitesimal generator" for A. It is interesting and mathematically significant to compare the algebraic properties of A and B. The key property for this comparison is the determinant equation
Det(eB) = etr(B)
where tr(B) denotes the trace of B. (One way to prove this identity is to use the Jordan canonical form for the matrix and the fact that similar matrices have the same trace and determinant.)
For example, if Det(eB) = 1 then we need that tr(B)=0. This means that elements of Sl(n) are the exponentials of matrices with trace equal to zero.
Let sl(n) denote the set of n x n matrices with trace equal to zero. The set sl(n) is not closed under matrix multiplication, but it is closed under the Lie bracket (or commutator) operation [B,C]=BC-CB.
If tr(B) = tr(C)=0, then
tr[B,C] = tr(BC-CB) = tr(BC) - tr(CB) = tr(BC)-tr(BC) = 0
(since tr(BC) = tr(CB) for any matrices B and C). Thus, if B and C belong to sl(n), then [B,C] also belongs to sl(n). This closure under the bracket operation leads directly to the notion of a Lie algebra.
Definition. A Lie algebra is a vector space L over a field F that is closed under a binary operation, called the Lie bracket and denoted by [B,C] for B and C in L. The bracket is assumed to satisfy the following axioms.
1. [X,Y] = -[Y,X] for all X and Y in L.
2. [aX+bY,Z] = a[X,Z] + b[Y,Z] for all a and b in F and X,Y,Z in L.
3. [X,[Y,Z]] + [Z,[X,Y]] + [Y,[Z,X]] = 0.
This last identity is called the Jacobi identity. It is easy to verify that the bracket operation [B,C]=BC - CB on the vector space of all n x n matrices over F (e.g. F=R) satisfies the axioms given above. Thus, we have so far seen that sl(n) is a Lie algebra that is naturally associated with the group of matrices Sl(n). In fact, sl(n) generates Sl(n) by exponentiation.
There is a general pattern. Each matrix group has its corresponding Lie algebra. The classification of matrix groups is simplified by a corresponding classification of Lie algebras. As a result, the Lie algebras are a subject in their own right. It has often happened that Lie algebras are connected mathematically with subjects different from their original roots in group theory.
In our context the Lie algebras turn out to be related to the formation of weight systems for Vassiliev invariants. One way to see this is to just take the case of matrix Lie algebras with commutator brackets and interpret diagrammatically the formula that states that the Lie algebra is closed under the bracket operation. This formula states that there is a basis {T1,T2,...,Tm} for the Lie algebra as a vector space over F such that each Ta is an n x n matrix and such that
TaTb - TbTa = fabcTc
where fabc is a set of constants in F depending on the three indices a,b,c (running from 1 to n). The right hand side of this equation connotes a summation over all values of the index c=1,...,n. The left hand side is the commutator of Ta and Tb for any given choice of a and b.
In Figure 39 we have diagrammed this equation using the conventions for diagrammatic matrix multiplication explained in this section. The structure constants fabc are represented by a graphical vertex with three lines attached to it, one for a, one for b and one for c. For the purpose of discussion,we shall assume that fabc is dependent only on the cyclic order of abc. It is convenient to regard the graphical vertex as representing a "tensor" that has this cyclic invariance since this means that we can slide the diagram for the structure constant tensor around in the plane so long as we keep the cyclic order of its legs unchanged. Such bases can be obtained in many cases of matrix Lie algebras, and the results that we outline can be generalised in any case.
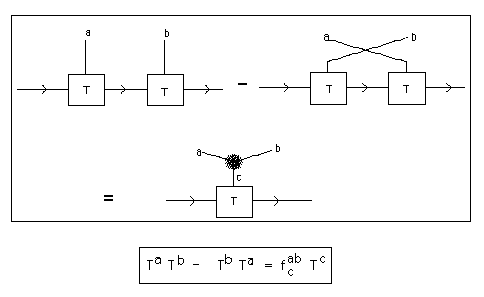
Figure 39
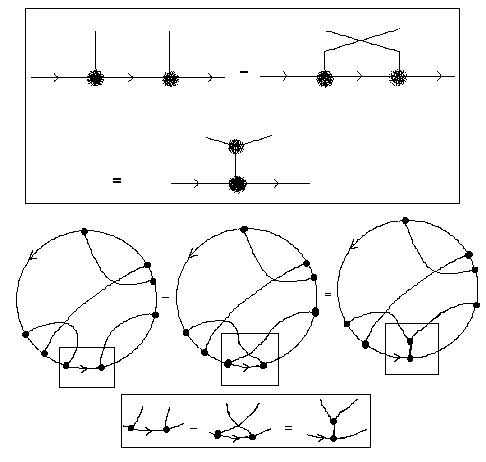
Figure 40
Now view Figure 40. You will see, first, a formal version of the commutator relation of Figure 39, except that the labels and indices have been removed and the boxes for matrix elements have been replaced by graphical vertices. Imagine that the terms in this formal version of the commutator relation are parts of chord diagrams as illustrated with examples in this figure. In other words, recall the method of chord diagrams from the last section and imagine that along with the chords there are also trivalent graphical vertices among the chords, and that these vertices are related to commutators as shown in the Figure. Finally, view Figure 41 and you will see a formal derivation of the four term relation for chord diagrams from the diagrammatic commutator identity.
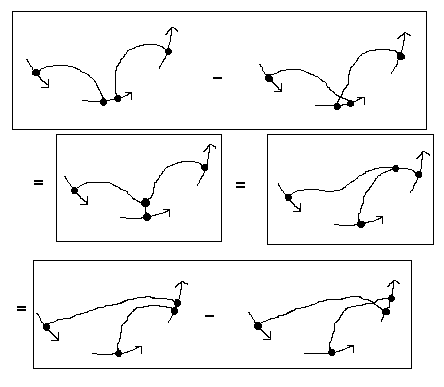
Figure 41
This means that the four-term relation, that we derived from topological considerations in the last section, is intimately related to the basic structure of a Lie algebra. This is the essence of the relationship of Vassiliev invariants with Lie algebras and their generalisations.
Concretely, the relationship we have just described means that it is possible to construct weight systems for Vassiliev invariants by using matrix Lie algebras. To see how this works view Figure 42. Here we have indicated a chord diagram D and a corresponding diagram involving matrices Ta from a Lie algebra basis. The second diagram represents the sum of traces wt(D) = Žtr(TaTbTcTaTbTc) where we are summing over all values for the indices a, b and c. This second diagram represents the weight, wt(D), that is assigned to the first diagram. It follows from our considerations that this weight system satisfies the four term relation and hence, by the Theorem of Kontsevich [BAR95], is the top row evaluation for a Vassiliev invariant.
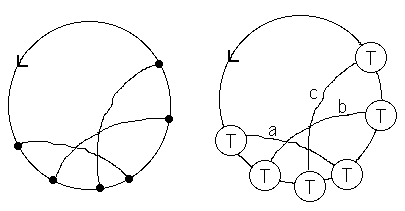
Figure 42
This section has been a sketch of the amazing and deep connection between Lie algebras and invariants of knots and links. The territory is even more surprising as one explores it further. First of all, it should be clear from what we have said that what is really needed here is an appropriate generalisation of Lie algebras. In fact, prior to the discovery of the Vassiliev invariants, a very remarkable such generalisation called "quantum groups" was discovered through work in statistical mechanics and was applied to knot theory. It was already known that quantum groups provided a strong connection between Lie algebras and their generalisations and invariants of knots and links. Now the matter of finding all weight systems challenges the resources of quantum groups and it is not known if all Vassiliev invariants can be built through the quantum groups.
In the next few sections we shall discuss the physical background behind many of the mathematical ideas discussed so far in this introduction to knot invariants.
VIII. A Quick Review of Quantum Mechanics
To recall principles of quantum mechanics it is useful to have a quick historical recapitulation. Quantum mechanics really got started when DeBroglie introduced the fantastic notion that matter (such as an electron) is accompanied by a wave that guides its motion and produces interference phenomena just like the waves on the surface of the ocean or the diffraction effects of light going through a small aperture.
DeBroglie’s idea was successful in explaining the properties of atomic spectra. In this domain, his wave hypothesis led to the correct orbits and spectra of atoms, formally solving a puzzle that had been only described in ad hoc terms by the preceding theory of Niels Bohr. In Bohr’s theory of the atom, the electrons are restricted to move only in certain elliptical orbits. These restrictions are placed in the theory to get agreement with the known atomic spectra, and to avoid a paradox! The paradox arises if one thinks of the electron as a classical particle orbiting the nucleus of the atom. Such a particle is undergoing acceleration in order to move in its orbit. Accelerated charged particles emit radiation. Therefore the electron should radiate away its energy and spiral into the nucleus! Bohr commanded the electron to only occupy certain orbits and thereby avoided the spiral death of the atom - at the expense of logical consistency.
DeBroglie hypothesised a wave associated with the electron and he said that an integral multiple of the length of this wave must match the circumference of the electron orbit. Thus, not all orbits are possible, only those where the wave pattern can "bite its own tail". The mathematics works out, providing an alternative to Bohr’s picture.
DeBroglie had waves, but he did not have an equation describing the spatial distribution and temporal evolution of these waves. Such an equation was discovered by Erwin Schrodinger. Schrodinger relied on inspired guesswork, based on DeBroglie’s hypothesis and produced a wave equation, known ever since as the Schrodinger equation. Schrodinger’s equation was enormously successful, predicting fine structure of the spectrum of hydrogen and many other aspects of physics. Suddenly a new physics, quantum mechanics, was born from this musical hypothesis of DeBroglie.
Along with the successes of quantum mechanics came a host of extraordinary problems of interpretation. What is the status of this wave function of Schrodinger and DeBroglie. Does it connote a new element of physical reality? Is matter "nothing but" the patterning of waves in a continuum? How can the electron be a wave and still have the capacity to instantiate a very specific event at one place and one time (such as causing a bit of phosphor to glow there on your television screen)? It came to pass that Max Born developed a statistical interpretation of the wave-function wherein the wave determines a probability for the appearance of the localised particulate phenomenon that one wanted to call an "electron". In this story the wavefunction y takes values in the complex numbers and the associated probability is y*y, where y* denotes the complex conjugate of y. Mathematically, this is a satisfactory recipe for dealing with the theory, but it leads to further questions about the exact character of the statistics. If quantum theory is inherently statistical, then it can give no complete information about the motion of the electron. In fact, there may be no such complete information available even in principle. Electrons manifest as particles when they are observed in a certain manner and as waves when they are observed in another, complementary manner. This is a capsule summary of the view taken by Bohr,Heisenberg and Born. Others, including DeBroglie, Einstein and Schrodinger, hoped for a more direct and deterministic theory of nature.
As we shall see, in the course of this essay, the statistical nature of quantum theory has a formal side that can be exploited to understand the topological properties of such mundane objects as knotted ropes in space and spaces constructed by identifying the sides of polyhedra. These topological applications of quantum mechanical ideas are exciting in their own right. They may shed light on the nature of quantum theory itself.
In this section we review a bit of the mathematics of quantum theory. Recall the equation for a wave:
f(x,t) = sin((2p/l)(x-ct)).
With x interpreted as the position and t and as the time, this function describes a sinusoidal wave travelling with velocity c. We define the wave number k= 2p/l and the frequency w = (2pc/l) where l is the wavelength. Thus we can write f(x,t) = sin(kx - wt). Note that the velocity, c, of the wave is given by the ratio of frequency to wave number, c=w/k.
DeBroglie hypothesised two fundamental relationships: between energy and frequency, and between momentum and wave number. These relationships are summarised in the equations
E = hw,
p=hk,
where E denotes the energy associated with a wave and p denotes the momentum associated with the wave. Here h = h/2ê where h is Planck’s constant.
For DeBroglie the discrete energy levels of the orbits of electrons in an atom of hydrogen could be explained by restrictions on the vibrational modes of waves associated with the motion of the electron. His choices for the energy and the momentum in relation to a wave are not arbitrary. They are designed to be consistent with the notion that the wave or wave packet moves along with the electron. That is, the velocity of the wave-packet is designed to be the velocity of the "corresponding" material particle.
It is worth illustrating how DeBroglie’s idea works. Consider two waves whose frequencies are very nearly the same. If we superimpose them (as a piano tuner superimposes his tuning fork with the vibration of the piano string), then there will be a new wave produced by the interference of the original waves. This new wave pattern will move at its own velocity, different (and generally smaller) than the velocity of the original waves. To be specific, let
f(x,t) = sin(kx - wt) and g(x,t) = sin(k’x - w’t).
Let
h(x,t) = sin(kx - wt) + sin(k’x - w’t) = = f(x,t) + g(x,t).
A little trigonometry shows that
h(x,t) = cos(((k-k’)/2)x -((w-w’)/2)t)sin(((k+k’)/2)x -((w+w’)/2)t).
If we assume that k and k’ are very close and that w and w’ are very close, then (k+k’)/2 is approximately k, and (w+w’)/2 is approximately w. Thus h(x.t) can be represented by
H(x.t) = cos((dk/2)x -(dw/2)t) f(x,t)
where dk=(k-k’)/2 and dw=(w-w’)/2. This means that the superposition, H(x,t), behaves as the waveform f(x,t) carrying a slower-moving "wave-packet" G(x,t)=cos((dk/2)x -(dw/2)t).
See Figure 43.
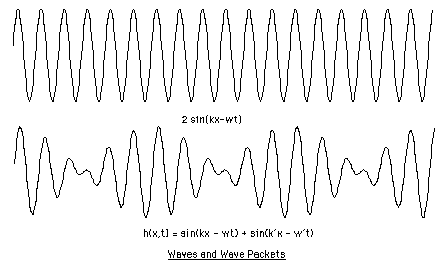
Figure 43
Since the wave packet (seen as the clumped oscillations in Figure 43) has the equation G(x,t)=cos((dk/2)x -(dw/2)t), we see that that the velocity of this wave packet is vg = dw/dk. Recall that wave velocity is the ratio of frequency to wave number. Now according to DeBroglie,
E = hw and p=hk, where E and p are the energy and momentum associated with this wave packet. Thus we get the formula vg = dE/dp. In other words, the velocity of the wave-packet is the rate of change of its energy with respect to its momentum. Now this is exactly in accord with the well-known classical laws for a material particle! For such a particle,
E = mv2/2 and p=mv. Thus E=p2/2m and dE/dp = p/m = v.
It is this astonishing concordance between the simple wave model and the classical notions of energy and momentum that initiated the beginnings of quantum theory.
Schrodinger’s Equation
Schrodinger answered the question:
Where is the wave equation for DeBroglie’s waves?
Writing an elementary wave in complex form
y = y(x,t) = exp(i(kx - wt)),
we see that we can extract DeBroglie’s energy and momentum by differentiating:
ih_y/_t = Ey and -ih_y/_x = py.
This led Schrodinger to postulate the identification of dynamical variables with operators so that the first equation ,
ih_y/_t = Ey,
is promoted to the status of an equation of motion while the second equation becomes the definition of momentum as an operator:
p = -ih_/_x .
Once p is identified as an operator, the numerical value of momentum is associated with an eigenvalue of this operator, just as in the example above. In our example py = hky.
In this formulation, the position operator is just multiplication by x itself. Once we have fixed specific operators for position and momentum, the operators for other physical quantities can be expressed in terms of them. We obtain the energy operator by substitution of the momentum operator in the classical formula for the energy:
E = (1/2)mv2 + V
E = p2/2m + V
E = -(h2/2m)_2/_x2 + V.
Here V is the potential energy, and its corresponding operator depends upon the details of the application.
With this operator identification for E, Schrodinger’s equation
ih_y/_t = -(h2/2m)_2y/_x2 + Vy
is an equation in the first derivatives of time and in second derivatives of space. In this form of the theory one considers general solutions to the differential equation and this in turn leads to excellent results in a myriad of applications.
In quantum theory, observation is modelled by the concept of eigenvalues for corresponding operators. The quantum model of an observation is a projection of the wave function into an eigenstate.
An energy spectrum {Ek} corresponds to wave functions y satisfying the Schrodinger equation, such that there are constants Ek with Ey = Eky. An observable (such as energy) E is a Hermitian operator on a Hilbert space of wavefunctions. Since Hermitian operators have real eigenvalues, this provides the link with measurement for the quantum theory.
It is important to notice that there is no mechanism postulated in this theory for how a wave function is "sent" into an eigenstate by an observable. Just as mathematical logic need not demand causality behind an implication between propositions, the logic of quantum mechanics does not demand a specified cause behind an observation.
This absence of an assumption of causality in logic does not obviate the possibility of causality in the world. Similarly, the absence of causality in quantum observation does not obviate causality in the physical world. Nevertheless, the debate over the interpretation of quantum theory has often led its participants into asserting that causality has been demolished in physics.
Note that the operators for position and momentum satisfy the equation xp - px = hi. This corresponds directly to the equation obtained by Heisenberg, on other grounds, that dynamical variables can no longer necessarily commute with one another. In this way, the points of view of DeBroglie, Schrodinger and Heisenberg came together, and quantum mechanics was born. In the course of this development, interpretations varied widely. Eventually, physicists came to regard the wave function not as a generalised wave packet, but as a carrier of information about possible observations. In this way of thinking y*y (y* denotes the complex conjugate of y.) represents the probability of finding the "particle" (A particle is an observable with local spatial characteristics.) at a given point in spacetime.
Dirac Brackets
We now discuss Dirac’s notation, <a|b>, [D]. In this notation <a| and |b> are vectors and covectors respectively. <a|b> is the evaluation of <a| by |b>, hence it is a scalar, and in ordinary quantum mechanics it is a complex number. One can think of this as the amplitude for the state to begin in "a" and end in "b". That is, there is a process that can mediate a transition from state a to state b. Except for the fact that amplitudes are complex valued, they obey the usual laws of probability. This means that if the process can be factored into a set of all possible intermediate states c1, c2, ..., cn , then the amplitude for a--->b is the sum of the amplitudes for a--->ci--->b. Meanwhile, the amplitude for a--->ci--->b is the product of the amplitudes of the two subconfigurations a--->ci and ci--->b. Formally we have
<a|b> = S <a|ci><ci|b>
where the summation is over all the intermediate states i=1, ..., n.
In general, the amplitude for mutually disjoint processes is the sum of the amplitudes of the individual processes. The amplitude for a configuration of disjoint processes is the product of their individual amplitudes.
Dirac’s division of the amplitudes into bras <a| and kets |b> is done mathematically by taking a vector space V (a Hilbert space, but it can be finite dimensional) for the bras: <a| belongs to V. The dual space V* is the home of the kets. Thus |b> belongs to V* so that |b> is a linear mapping |b>:V -----> C where C denotes the complex numbers. We restore symmetry to the definition by realising that an element of a vector space V can be regarded as a mapping from the complex numbers to V. Given <a|: C -----> V, the corresponding element of V is the image of 1 (in C) under this mapping. In other words, <a|(1) is a member of V. Now we have <a| :C -----> V and |b> : V -----> C. The composition <a| |b> = <a|b> : C -----> C is regarded as an element of C by taking the specific value <a|b>(1). The complex numbers are regarded as the "vacuum", and the entire amplitude <a|b> is a "vacuum to vacuum" amplitude for a process that includes the creation of the state a, its transition to b, and the annihilation of b to the vacuum once more.
Dirac notation has a life of its own.
Let P = |y><x|.
Let <x| |y> = <x|y>.
Then PP = |y><x| |y><x| = |y> <x|y> <x| = <x|y> P.
Up to a scalar multiple, P is a projection operator. That is, if we let
Q= P/<x|y>, then QQ = PP/<x|y><x|y> = <x|y>P/<x|y><x|y> = P/<x|y> = Q.
Thus QQ=Q. In this language, the completeness of intermediate states becomes the statement that a certain sum of projections is equal to the identity: Suppose that Ži |ci><ci| = 1 (summing over i)
with <ci|ci>=1 for each i. Then
<a|b>
= <a| |b>
= <a| S|ci><ci| |b>
= S <a| |ci><ci| |b>
= S <a|ci><ci|b>.
Iterating this principle of expansion over a complete set of states leads to the most primitive form of the Feynman integral [FH]. Imagine that the initial and final states a and b are points on the vertical lines x=0 and x=n+1 respectively in the x-y plane, and that (c(k)i(k) , k) is a given point on the line x=k for 0<i(k)<m. Suppose that the sum of projectors for each intermediate state is complete. That is, we assume that following sum is equal to one, for each k from 1 to n-1:
|c(k)1><c(k)1| + ... + |c(k)m><c(k)m| = 1.
Applying the completeness iteratively, we obtain the following expression for the amplitude <a|b>:
<a|b> = S <a|c(1)i(1)><c(1)i(1)|c(2)i(2)> ... <c(n)i(n)|b>
where the sum is taken over all i(k) ranging between 1 and m, and k ranging between 1 and n. Each term in this sum can be construed as a combinatorial path from a to b in the two dimensional space of the x-y plane. Thus the amplitude for going from a to b is seen as a summation of contributions from all the "paths" connecting a to b. Feynman used this description to produce his famous path integral expression for amplitudes in quantum mechanics. His path integral takes the form
S
dP exp(iS)where i is the square root of minus one, the integral is taken over all paths from point a to point b, and S is the action for a particle to travel from a to b along a given path. For the quantum mechanics associated with a classical (Newtonian) particle the action S is given by the integral along the given path from a to b of the difference T-V where T is the classical kinetic energy and V is the classical potential energy of the particle.
The beauty of Feynman’s approach to quantum mechanics is that it shows the relationship between the classical and the quantum in a particularly transparent manner. Classical motion corresponds to those regions where all nearby paths contribute constructively to the summation. This classical path occurs when the variation of the action is null. To ask for those paths where the variation of the action is zero is a problem in the calculus of variations, and it leads directly to Newton’s equations of motion. Thus with the appropriate choice of action, classical and quantum points of view are unified.
The drawback of this approach lies in the unavailability at the present time of an appropriate measure theory to support all cases of the Feynman integral.
To summarise, Dirac notation shows at once how the probabilistic interpretation for amplitudes is tied with the vector space structure of the space of states of the quantum mechanical system. Our strategy for bringing forth relations between quantum theory and topology is to pivot on the Dirac bracket. The Dirac bracket intermediates between notation and linear algebra. In a very real sense, the connection of quantum mechanics with topology is an amplification of Dirac notation.
The next two sections discuss how topological invariants in low dimensional topology are related to amplitudes in quantum mechanics. In these cases the relationship with quantum mechanics is primarily mathematical. Ideas and techniques are borrowed. It is not yet clear what the effect of this interaction will be on the physics itself.
IX. Knot Amplitudes
At the end of the last section we said: the connection of quantum mechanics with topology is an amplification of Dirac notation.
Figure 44
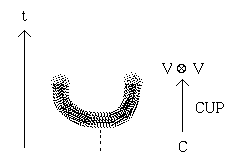
Figure 45
and their subsequent annihilation (Figure 46).

Figure 46
In accord with our previous description, we could divide the circle into these two parts (creation(a) and annihilation (b)) and consider the amplitude <a|b>. Since the diagram for the creation of the two particles ends in two separate points, it is natural to take a vector space of the form VVV (the tensor product of V with V) as the target for the bra and as the domain of the ket.
We imagine at least one particle property being catalogued by each dimension of V. For example, a basis of V could enumerate the spins of the created particles. If {ea} is a basis for V then
{eaVeb} forms a basis for VVV. The elements of this new basis constitute all possible combinations of the particle properties. Since such combinations are multiplicative, the tensor product is the appropriate construction.
In this language the creation ket is a map cup,
cup = <a| : C -----> VVV,
and the annihilation bra is a mapping cap,
cap= |b> : VVV -----> C.
The first hint of topology comes when we realise that it is possible to draw a much more complicated simple closed curve in the plane that is nevertheless decomposed with respect to the vertical direction into many cups and caps. In fact, any non-selfintersecting differentiable curve can be rigidly rotated until it is in general position with respect to the vertical. It will then be seen to be decomposed into these minima and maxima. Our prescriptions for amplitudes suggest that we regard any such curve as an amplitude via its description as a mapping from C to C.
Each simple closed curve gives rise to an amplitude, but any simple closed curve in the plane is isotopic to a circle, by the Jordan Curve Theorem. If these are topological amplitudes, then they should all be equal to the original amplitude for the circle. Thus the question: What condition on creation and annihilation will insure topological amplitudes? The answer derives from the fact that all isotopies of the simple closed curves are generated by the cancellation of adjacent maxima and minima as illustrated in Figure 47.
Figure 47
In composing mappings it is necessary to use the identifications
(VVV) VV = VV (VVV) and VVk=kVV=V.
Thus in Figure 47, the composition on the left is given by
V = VVk --1cup--> VV (VVV) = (VVV) VV --cap1--> kVV = V.
This composition must equal the identity map on V (denoted 1 here) for the amplitudes to have a proper image of the topological cancellation.
This condition is said very simply by taking a matrix representation for the corresponding operators. Specifically, let {e1, e2, ..., en} be a basis for V. Let eab = ea V eb denote the elements of the tensor basis for
VVV. Then there are matrices Mab and Mab such that
cup(1) = S Mabeab with the summation taken over all values of a and b from 1 to n. Similarly, cap is described by cap(eab) = Mab. Thus the amplitude for the circle is
cap[cup(1)] = cap S Mabeab = S MabMab.
In general, the value of the amplitude on a simple closed curve is obtained by translating it into an "abstract tensor expression" in the Mab and Mab, and then summing over these products for all cases of repeated indices.
Figure 48
Returning to the topological conditions we see that they are just that the matrices (Mab) and (Mab) are inverses in the sense that
S
MaiMib = Iab and S MaiMib = Iab are identity matrices.In the Figure 48, we show the diagrammatic representative of the equation S MaiMib = Iab.
In the simplest case cup and cap are represented by 2 x 2 matrices. The topological condition implies that these matrices are inverses of each other. Thus the problem of the existence of topological amplitudes is very easily solved for simple closed curves in the plane.
Now we go to knots and links. Any knot or link can be represented by a picture that is configured with respect to a vertical direction in the plane. The picture will decompose into minima (creations) maxima (annihilations) and crossings of the two types shown below. (Here I consider knots and links that are unoriented. They do not have an intrinsic preferred direction of travel.) See Figure 49. In Figure 49, next to each of the crossings we have indicated mappings of VVV to itself , called R and R-1 respectively. These mappings represent the transitions corresponding to these elementary configurations.
Figure 49
That R and R-1 really must be inverses follows from the isotopy shown in Figure 50 (This is the second Reidemeister move.)
Figure 50
We now have the vocabulary of cup,cap, R and R-1. Any knot or link can be written as a composition of these fragments, and consequently a choice of such mappings determines an amplitude for knots and links. In order for such an amplitude to be topological we want it to be invariant under the list of local moves on the diagrams shown in Figure 51. These moves are an augmented list of the Reidemeister moves (See Figure 4 in section 2), adjusted to take care of the fact that the diagrams are arranged with respect to a given direction in the plane.
The equivalence relation generated by these moves is called regular isotopy. It is one move short of the relation known as ambient isotopy. The missing move is the first Reidemeister move shown in Figure 4 of section 2.
In the first Reidemeister move, a curl in the diagram is created or destroyed. Ambient isotopy (generated by all the Reidemeister moves) corresponds to the full topology of knots and links embedded in three dimensional space. Two link diagrams are ambient isotopic via the Reidemeister moves if and only if there is a continuous family of embeddings in three dimensions leading from one link to the other. The moves give a combinatorial reformulation of the spatial topology of knots and links.
By ignoring the first Reidemeister move, we allow the possibility that these diagrams can model framed links, that is links with a normal vector field or,equivalently, embeddings of curves that are thickened into bands. It turns out to be fruitful to study invariants of regular isotopy. In fact, one can usually normalise an invariant of regular isotopy to obtain an invariant of ambient isotopy. We have already discussed this phenomenon with the bracket polynomial in section 5.
As the reader can see, we have already discussed the algebraic meaning of Moves 0. and 2. The other moves translate into very interesting algebra. Move 3., when translated into algebra, is the famous Yang-Baxter equation. The Yang-Baxter equation occurred for the first time in problems related to exactly solved models in statistical mechanics
(See [BA].). All the moves taken together are directly related to the axioms for a quasi-triangular Hopf algebra (aka quantum group). We shall not go into this connection here.
There is an intimate connection between knot invariants and the structure of generalised amplitudes, as we have described them in terms of vector space mappings associated with link diagrams. This strategy for the construction of invariants is directly motivated by the concept of an amplitude in quantum mechanics. It turns out that the invariants that can actually be produced by this means (that is by assigning finite dimensional matrices to the caps, cups and crossings) are incredibly rich. They encompass, at present, all of the known invariants of polynomial type (Alexander polynomial, Jones polynomial and their generalisations.).
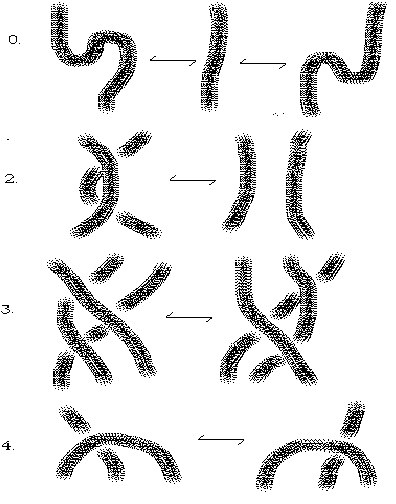
Figure 51 - Augmented Reidemeister Moves for Regular Isotopy
It is now possible to indicate the construction of the Jones polynomial via the bracket polynomial as an amplitude, by specifying its matrices.
The cups and the caps are defined by (Mab) = (Mab) = M where M is the 2 x 2 matrix (with ii=-1)
Note that MM = I where I is the identity matrix. Note also that the amplitude for the circle is
S
MabMab = S MabMab = S (Mab)2= (iA)2 + (-iA-1)2 = - A2 - A-2.
The matrix R is then defined by the equation
Rabcd = AMabMcd + AIacIbd .
Since, diagrammatically, we identify R with a (right handed)
crossing, this equation can be written diagrammatically as
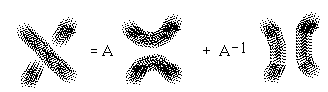
Taken together with the loop value of A2 - A-2,
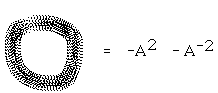
these equations can be regarded as a recursive algorithm for computing the amplitude.
This algorithm is the bracket state model for the (unnormalised) Jones polynomial [KA87]. This model can be studied on its own grounds as we have already done in section 5.
X. Topological Quantum Field Theory - First Steps
In order to further justify the idea of topology in relation to the amplification of Dirac notation, consider the following scenario. Let M be a 3-dimensional manifold; that is, a space that is locally homeomorphic to Euclidean three dimensional space. Suppose that F is a closed orientable surface inside M dividing M into two pieces M1 and M2. These pieces are 3-manifolds with boundary. They meet along the surface F. Now consider an amplitude <M1|M2> = Z(M). The form of this amplitude generalises our previous considerations, with the surface F constituting the distinction between the "preparation" M1 and the "detection" M2. This generalisation of the Dirac amplitude <a|b> amplifies the notational distinction consisting in the vertical line of the bracket to a topological distinction in a space M. The amplitude Z(M) will be said to be a topological amplitude for M if it is a topological invariant of the 3-manifold M. Note that a topological amplitude does not depend upon the choice of surface F that divides M.
From a physical point of view the independence of the topological amplitude on the particular surface that divides the 3-manifold is the most important property. An amplitude arises in the condition of one part of the distinction carved in the 3-manifold acting as "the observed" and the other part of the distinction acting as "the observer". If the amplitude is to reflect physical (read topological) information about the underlying manifold, then it should not depend upon this particular decomposition into observer and observed. The same remarks apply to 4-manifolds and interface with ideas in relativity. We mention 3-manifolds because it is possible to describe many examples of topological amplitudes in three dimensions. The matter of 4-dimensional amplitudes is a topic of current research. The notion that an amplitude be independent of the distinction producing it is prior to topology. Topological invariance of the amplitude is a convenient and fundamental way to produce such independence.
This sudden jump to topological amplitudes has its counterpart in mathematical physics. In [WIT] Edward Witten proposed a formulation of a class of 3-manifold invariants as generalised Feynman integrals taking the form Z(M) where
Z(M) = SdAexp[(ik/4p)S(M,A)].
Here M denotes a 3-manifold without boundary and A is a gauge field (also called a gauge potential or gauge connection) defined on M. The gauge field is a one-form on M with values in a representation of a Lie algebra. The group corresponding to this Lie algebra is said to be the gauge group for this particular field. In this integral the "action" S(M,A) is taken to be the integral over M of the trace of the Chern-Simons three-form CS = AdA + (2/3)AAA. (The product is the wedge product of differential forms.)
Instead of integrating over paths, the integral Z(M) integrates over all gauge fields modulo gauge equivalence. This generalisation from paths to fields is characteristic of quantum field theory. Quantum field theory was designed in order to accomplish the quantisation of electromagnetism. In quantum electrodynamics the classical entity is the electromagnetic field. The question posed in this domain is to find the value of an amplitude for starting with one field configuration and ending with another. The analogue of all paths from point a to point b is "all fields from field A to field B".
Witten’s integral Z(M) is, in its form, a typical integral in quantum field theory. In its content Z(M) is highly unusual. The formalism of the integral, and its internal logic supports the existence of a large class of topological invariants of 3-manifolds and associated invariants of knots and links in these manifolds.
Invariants of three-manifolds were initiated by Witten as functional integrals in [WIT] and at the same time defined in a combinatorial way by Reshetikhin and Turaev in [RT2]. The Reshetikhin-Turaev definition proceeds in a way that is quite similar to the definition that we gave for the bracket model for the Jones polynomial in section 2. It is an amazing fact that Witten’s definition seems to give the very same invariants. We are not in a position to go into the details of this correspondence here. However, one theme is worth mentioning: For k large, the Witten integral is approximated by those gauge connections A for which S(M,A) has zero variation with respect to change in A. These are the so-called flat connections. It is possible in many examples to calculate this contribution via both the functional integral and by the combinatorial definition of Reshetikhin and Turaev. In all cases, the two methods agree (See e.g. [FG],[LR]). This is one of the pieces of evidence in a puzzle that everyone expects will eventually justify the formalism of the functional integral.
In order to obtain invariants of knots and links from Witten’s integral, one adds an extra bit of machinery to the brew. The new machinery is the Wilson loop. The Wilson loop is an exponentiated version of integrating the gauge field along a loop K. We take this loop K in three space to be an embedding (a knot) or a curve with transversal self-intersections. It is usually indicated by the symbolism tr(Pexp(SK A)).
Here the P denotes path ordered integration - that is we are integrating and exponentiating matrix valued functions, and one must keep track of the order of the operations. The symbol tr denotes the trace of the resulting matrix.
With the help of the Wilson loop function on knots and links, Witten [WIT] writes down a functional integral for link invariants in a 3-manifold M:
Z(M,K) = SdAexp[(ik/4p)S(M,A)] tr(Pexp(SK A)).
Here S(M,A) is the Chern-Simons Lagrangian, as in the previous discussion.
If one takes the standard representation of the Lie algebra of SU(2) as 2x2 complex matrices then it is a fascinating exercise to see that the formalism of Z(S3,K) (S3 denotes the three-dimensional sphere.) yields up the original Jones polynomial with the basic properties as discussed in section 1. See Witten’s paper or [WIT] or [KA95] for discussions of this part of the heuristics.
This approach to link invariants crosses boundaries between different methods. There are close relations between Z(S3,K) and the invariants defined by Vassiliev (See [BAR95],[KA95].), to name one facet of this complex crystal.
Links and the Wilson loop
We shall now indicate an analysis the formalism of this functional integral that reveals quite a bit about its role in knot theory. This analysis depends upon some key facts relating the curvature of the gauge field to both the Wilson loop and the Chern-Simons Lagrangian. To this end, let us recall the local coordinate structure of the gauge field A(x), where x is a point in three-space. We can write A(x) = Aak(x)Tadxk where the index a ranges from 1 to m with the Lie algebra basis {T1, T2, T3, ..., Tm}. The index k goes from 1 to 3. For each choice of a and k, Aak(x) is a smooth function defined on three-space. In A(x) we sum over the values of repeated indices. The Lie algebra generators Ta are actually matrices corresponding to a given representation of an abstract Lie algebra.
Difference Formula.
One can deduce a difference formula for the Witten invariants from the formal properties of the functional integral. Let K+ and K- denoting knots that differ at a single crossing with + and - signs respectively, and K## the result of replacing the crossing by a transverse singularity ( i.e. with distinct tangent directions for the two local curve segments). We take K# to denote the insertion of a graphical node at the transverse crossing, as we have done in our discussion of the Vassiliev invariant. The notation K## indicates that the curve intersects itself in space at one point. Let K##TaTa denote the result of placing the matrices of the Lie algebra basis into the Wilson line at the singular crossing as shown in Figure 52.
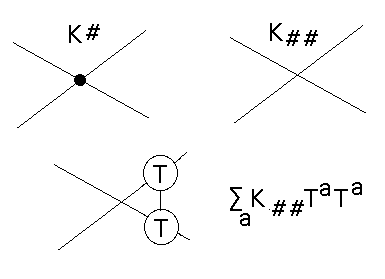
Figure 52
These matrices become part of the big matrix product that generates the Wilson line. Then, up to order (1/k) one has the difference relation (See [KA95].)
Z(K+) - Z(K-) = (4pi/k) Z(K##TaTa).
This formula is the key to unwrapping many properties of the knot invariants.
Graph Invariants and Vassiliev Invariants
Recall, from section 6, that V(G) is a Vassiliev invariant if
VK+ - VK- =VK# .
V(G) is said to be of finite type k if V(G) = 0 whenever #(G) >k where #(G) denotes the number of 4-valent nodes in the graph G. See section 6.
With this definition in hand, lets return to the invariants derived from the functional integral Z(K). We have that
Z(K+) - Z(K-) = (4pi/k) Z(K##TaTa).
This formula tells us that for the Vassiliev invariant associated with Z we have
Z(K#) = (4pi/k)Z(K##TaTa).
Furthermore, if Vj(K) denotes the coefficient of (4pi/k)j in the expansion of Z(K) in powers of (1/k), then the ambient difference formula implies that (1/k)j divides Z(G) when G has j or more nodes. Hence Vj(G) = 0 if G has more than j nodes. Therefore Vj(K) is a Vassiliev invariant of finite type. (This result was proved by Birman and Lin [BIL] by different methods and by Bar-Natan [BAR95] by methods equivalent to ours.)
The fascinating thing is that the ambient difference formula , appropriately interpreted, actually tells us how to compute Vk(G) when G has k nodes.
This result is equivalent to the description of weight systems derived from Lie algebras that we described in section 7. Thus the approach to link invariants via the functional integral motivates and explains the fundamental structure of Vassiliev invariants.
This deep relationship between topological invariants in low dimensional topology and quantum field theory in the sense of Witten’s functional integral is really still in its infancy. There will be many surprises in the future as we discover that what has so far been uncovered is only the tip of an iceberg.
References
[AW] Y.Akutsu and M.Wadati. Knot invariants and critical statistical systems. J.Phys.Soc.Japan 56 (1987)839-842.
[AL] J.W.Alexander. Topological invariants of knots and links.Trans.Amer.Math.Soc. 20 (1923) .275-306.
[AT1] M.F. Atiyah. Geometry of Yang-Mills Fields. Academia Nazionale dei Lincei Scuola Superiore Lezioni Fermiare, Pisa (1979).
[AT2] M.F. Atiyah. The Geometry and Physics of Knots. Cambridge University Press (1990).
[BAE94] J. Baez and J.P. Muniain. Gauge Fields, Knots and Gravity. World Sci. Press (1994).
[BAR95] D. Bar-Natan, On the Vassiliev Knot invariants.
Topology,Vol.34,No.2 (1995), pp. 423-472.
[BCW] W.R. Bauer, F.H.C. Crick and J.H. White. Supercoiled DNA. Scientific American. Vol.243. July 1980. pp. 118-133.
[BA] R.J. Baxter. Exactly Solved Models in Statistical Mechanics. Acad. Press (1982).
[BAY] B. F. Bayman. Theory of Hitches. Amer. J. Physics. Vol.145., No. 2. (1977), pp. 185-190.
[BP] H.J. Bernstein and A.V. Phillips. Fiber bundles and quantum theory. Scientific American. Vol. 245. No.1. July 1981, pp. 122-137.
[BL] L.C. Biedenharn and J.D. Louck. Angular Momentum in
Quantum Physics- Theory and Application. (Encyclopedia
of Mathematics and its Applications). Cambridge University Press
(1979).
[BIL] J. Birman and X.S.Lin. Knot polynomials and Vassiliev’s invariants. Invent. Math.
[CON] J.H.Conway.An enumeration of knots and links and some of their algebraic properties. Computational Problems in Abstract Algebra . Pergamon Press,New York(1970),329-358.
[CSS] N.R. Cozzarelli, S.J. Spengler, A.Stasiak. The stereostructure of knots and catenanes produced by phage l integrative recombination: implications for mechanism and DNA structure. Cell. Vol.42. (1985). pp. 325-334.
[CF] R.H.Crowell and R.H.Fox. Introduction to Knot Theory. Blaisdell Pub. Co. (1963).
[D] P.A.M. Dirac. Principles of Quantum Mechanics. Oxford University Press (1958).
[DRIN] V.G.Drinfeld. Quantum Groups, Proc.Intl.Congress Math.,Berkeley,Calif.USA(1986).789-820.
[ES] C. Ernst and D.W. Sumners. A calculus for rational tangles: applications to DNA recombination. Math. Proc. Camb. Phil. Soc. 108 (1990). pp. 489-515.
[FRT] L.D.Faddeev, N.Yu.Reshetikhin, L.A.Takhtajan. Quantization of Lie groups and Lie algebras. LOMI Preprint E-14-87, Steklov Mathematical Institute, Leningrad, USSR.
[FR] R. A. Fenn and C.P. Rourke. Racks and links in codimension two. Journal of Knot Theory and Its Ramifications. Vol. 1, No. 4 (1992), 343-406.
[FE] R. P. Feynman. Theory of Fundamental Processes. W.A. Benjamin Pub. (1961).
[FH] R. Feynman and A.R. Hibbs. Quantum Mechanics and Path Integrals. McGraw Hill (1965).
[FOX] R.H. Fox. A quick trip through knot theory. In Topology of 3-Manifolds. ed. by M.K. Fort Jr. . Prentice Hall (1962). pp. 120-167.
[FK] G.K.Francis and L.H. Kauffman. Air on the Dirac Strings. ( to appear in the proceedings of conference held in honor of Wilhelm Magnus - New York City -1992)
[FG] D. Freed and R. Gompf. Computer calculations of Witten’s 3-manifold invariants. Comm. Math. Phys. 41, pp. 79-117 (1991).
[F] P.Freyd,D.Yetter,J.Hoste,W.B.R.Lickorish,K.C.Millett,A.Ocneanu .A new polynomial invariant of knots and links. Bull.Amer.Math.Soc. 12 (1985) 239-246.
[FU] B. Fuller. Decomposition of the linking number of a closed ribbon: a problem from molecular biology. Proc. Natl. Acad. Sci. USA, Vol. 75. No.8. (1978). pp. 3557-3561.
[JO1] V.F.R. Jones. Index for subfactors. Invent. Math. 72 (1983). pp 1-25.
[JO2] V.F.R.Jones.A polynomial invariant for links via von Neumann algebras. Bull.Amer.Math.Soc. 129 (1985) 103-112.
[JO3] V.F.R.Jones. A new knot polynomial and von Neumann algebras. Notices of AMS 33 (1986) 219-225.
[JO4] V.F.R.Jones. Hecke algebra representations of braid groups and link polynomials. Ann. of Math. 126 (1987), pp. 335-338.
[JO5] V.F.R.Jones. On knot invariants related to some statistical mechanics models. Pacific J. Math., vol. 137, no. 2 (1989), pp. 311-334.
[JOY] D. Joyce. A classifying invariant of knots, the knot quandle. J. Pure Appl. Alg., 23, 37-65.
[K1] L.H.Kauffman.The Conway polynomial.Topology 20 (1980) 101-108.
[K2] L.H. Kauffman. Formal Knot Theory. Lecture Notes #115. Princeton University Press (1983).
[K3] L.H.Kauffman. State Models and the Jones Polynomial. Topology 26 (1987) 395-407.
[K4] L.H. Kauffman. On Knots. Annals of Mathematics Studies Number 115, Princeton University Press (1987).
[K5] L.H.Kauffman. New invariants in the theory of knots. Amer. Math. Monthly Vol.95, No.3, March 1988. pp 195-242.
[K6] L.H.Kauffman. Spin Networks and the Jones Polynomial. Twistor Newsletter No. 29. (1989) pp. 25-29.
[K7] L. H. Kauffman. Knots, abstract tensors, and the Yang-Baxter equation. In Knots, Topology and Quantum Field theories - Proceedings of the Johns Hopkins Workshop on Current Problems in Particle Theory 13. Florence (1989). ed. by L. Lussana. World Scientific Pub. (1989). pp. 179-334.
[K8] L.H.Kauffman.Statistical mechanics and the Jones polynomial. In Proceedings of the 1986 Santa Cruz conference on Artin's Braid Group. AMS Contemp. Math. Series. Vol. 78. (1989). pp. 263-297. reprinted in New Problems, Methods and Techniques in Quantum Field Theory and Statistical Mechanics. pp. 175-222. ed. by M. Rasetti. World Scientific Pub. (1990).
[K9] L.H.Kauffman. An invariant of regular isotopy. Trans. Amer. Math. Soc. Vol. 318. No. 2 (1990). pp. 417-471.
[K10] L.H. Kauffman. Knots and Physics , World Scientific Pub. (1991 , Second edition 1993).
[K11] L.H. Kauffman. Map Coloring, q-Deformed Spin Networks, and Turaev-Viro Invariants for 3-Manifolds. In the Proceedings of the Conference on Quantum Groups - Como, Italy June 1991 - edited by M. Rasetti - World Sci. Pub., Intl. J. Mod. Phys. B, Vol. 6, Nos. 11 & 12 (1992), pp. 1765 - 1794.
[K12] L.H.Kauffman and S. Lins. Temperley Lieb Recoupling Theory and Invariants of 3-Manifolds. Annals Study No.134. Princeton University Press (1994).
[K13] L.H.Kauffman.Invariants of graphs in three-space. Trans.Amer. Math.Soc. Vol. 311 No. 2 (Feb. 1989), 697-710.
[K14] L.H.Kauffman. Gauss codes, quantum groups and ribbon Hopf algebras. Reviews in Mathematical Physics, Vol. 5, No. 4 (1993), 735-773.
[K15] L.H. Kauffman. Knot Logic. In Knots and Applications. ed. by L.H. Kauffman. World Scientific Pub. Co. (1994)
[KR] L.H.Kauffman and D.E.Radford. Invariants of 3-manifolds derived from finite dimensional Hopf algebras. Journal of Knot Theory and its Ramifications, Vol.4, No.1 (1995), pp. 131-162.
[KA95] L. H. Kauffman. Functional integration and the theory of knots. J. Math. Phys. Vol. 36, No.5 (19950, pp. 2402-2429.
[KA96] L.H.Kauffman. Knots and Statistical Mechanics, Proceedings of Symposia in Applied Mathematics - The Interface of Knots and Physics (edited by L. Kauffman), Vol.51 (1996), pp. 1-87.
[KH] L. H. Kauffman and F. Harary, Knots and Graphs I, (in preparation).
[KI] T.P.Kirkman.The enumeration,description and construction of knots with fewer than 10 crossings. Trans. Royal Soc. Edin. 32(1865),281-309.
[KIRB] R. Kirby. A calculus for framed links in S3. Invent. Math., 45, 35-36. (1978)
[KM] R. Kirby and P. Melvin. On the 3-manifold invariants of Reshetikhin- Turaev for sl(2,C). Invent. Math., Vol. 105 (1991), pp. 473-545.
[KO] M. Kontsevich. Graphs, homotopical algebra and low dimensional topology. (preprint 1992).
[KR] A.N. Kirillov. and N.Y. Reshetikhin. Representations of the algebra Uq(sl2) , q-orthogonal polynomials and invariants of links. In Infinite Dimensional Lie Algebras and Groups. ed. by V.G. Kac. Adv. Ser. in Math. Phys. Vol. 7. (1988). pp. 285-338.
[LI] W. B. R. Lickorish. 3-Manifolds and the Temperley Lieb Algebra. Math. Ann. 290, 657-670 (1991).
[LIT] C.N.Little. Non-alternate +- knots. Trans. Royal Soc. Edin. 35 (1889) 663-664.
[LR] R. Lawrence and L. Rozansky, Witten-Reshetikhin-Turaev Invariants of Seifert Manifolds, (preprint 1997).
[MT] W. Menasco and M. Thistlethwaite. The classification of alternating links. Annals of Math. 138 (1993), 113-171.
[MUR1] K. Murasugi. The Jones polynomial and classical conjectures in knot theory. Topology, 26, 187-194. (1987).
[MUR2] K. Murasugi. Jones polynomials and classical conjectures in knot theory II. Math. Proc. Camb. Phil. Soc. 102 (1987). 317-318.
[MTW] C.W.Misner, K.S.Thorne and J.W.Wheeler. Gravitation. W.H. Freeman (1973).
[N] M.H.A. Newman. On a string problem of Dirac. J. London Math. Soc. 17 (1942). pp. 173-177.
[PT] J.H. Przytycki and P. Traczyk. Invariants of links of Conway type. Kobe J. Math. 4 (1987). pp. 115-139.
[R] J. Roberts. Skein theory and Turaev-Viro invariants. (preprint 1993).
[REI] K. Reidemeister. Knotentheorie. chelsea Pub. Co. N.Y. (1948). Copyright 1932. Julius Springer, Berlin.
[RES] N.Y.Reshetikhin. Quantized universal enveloping algebras, the Yang-Baxter equation and invariants of links, I and II. LOMI reprints E-4-87 and E-17-87, Steklov Institute, Leningrad, USSR.
[RT1] N.Y. Reshetikhin and V. Turaev. Ribbon graphs and their invariants derived from quantum groups. Comm. Math. Phys. 127 (1990). pp. 1-26.
[RT2] N.Y. Reshetikhin and V. Turaev. Invariants of Three Manifolds via link polynomials and quantum groups. Invent. Math. 103, 547-597 (1991).
[ROSS] M. Rosso. Groupes quantiques et modeles a vertex de V. Jones en theorie des noeuds. C.R.Scad.Sci.Paris t.307 (1988). pp. 207-210.
[ST] T. Stanford. Finite-type invariants of knots, links and graphs. (preprint 1992).
[S] D.W. Sumners. Untangling DNA. Math. Intelligencer. Vol. 12. No. 3. (1990). pp. 71-80.
[T] P.G.Tait.On Knots I,II,III.Scientific Papers Vol.I,Cambridge University Press.,London,1898,273-347.
[TH] M.B. Thistlethwaite. Kauffman's polynomial and alternating links. Topology 27 (1988). pp. 311-318.
[TM] W. Thomson (Lord Kelvin) . On vortex atoms. Philosophical magazine. 34. July 1867. pp. 15-24. Mathematical and Physical Papers, Vol. 4. Cambridge (1910).
[TU] V.G.Turaev. The Yang-Baxter equations and invariants of links. LOMI preprint E-3-87, Steklov Institute, Leningrad, USSR. Inventiones Math. 92 Fasc.3,527-553.
[TV] V.G. Turaev and O. Viro. State sum invariants of 3-manifolds and quantum 6j symbols. Topology, Vol. 31, No. 4, pp. 865-902 (1992).
[V] V. Vassiliev. Cohomology of knot spaces. In Theory of Singularities and Its Applications. (V.I.Arnold, ed.), Amer. Math. Soc. (1990), pp. 23-69.
[WA] K. Walker. On Witten's 3-Manifold Invariants. (preprint 1991).
[W] J. H. White. Self-linking and the Gauss integral in higher dimensionas. Amer. J. Math. Vol. 91. (1969). pp. 693-728.
[WIN] S. Winker. Quandles, Knot Invariants and the N-fold Branched Cover. Ph.D. Thesis, University of Illinos at Chicago (1984).
[WIT] E.Witten. Quantum field theory and the Jones polynomial. Commun.Math.Phys. 121 , 351-399 (1989).
[Wu] F.Y. Wu. Knot theory and statistical mechanics. Reviews of Modern Physics.Vol. 64. No. 4. October (1992), 1099-1129.
[YE] D. Yetter. Quantum groups and representations of monoidal categories. Math. Proc. Camb. Phil. Soc. 108 (1990). pp. 197-229.
[Z] A.B. Zamolodchikov. Factorized S matrices and lattice statistical systems. Soviet Sci. Reviews. PartA (1979-1980).