Fractals, Chaos and Complex Dynamics

A Research Experience for Undergraduates, UIC, August 2002

Marc Culler and Howard Masur

This material is based upon work supported by the National Science Foundation under Grant No. 9983703
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Puteţi citi această pagină web tradusă în limba română de Aleksandra Seremina şi azoft.com.

A major part of this REU program involved using computers to visualize and explore the mathematical ideas that we were studying.  This web page serves to describe and distribute the software that was used during the program. The software is distributed under the GNU General Public License.

About the software

This software is written in the Python programming language.  Python is an interpreted language with an elegant, clean syntax and can be easily extended to include modules written in other languages.  Python is an object oriented language which can be used interactively.  It is an easy language to learn, yet it can accommodate very sophisticated programmers. These were all features that were beneficial to us.

We generally used Python interactively.  The python modules that are included in this distribution typically define one python class.  The objects of these classes usually have a graphical component, so that creating the object causes an interactive window to open on the user's screen.  But the objects also have methods that can be used to modify the attributes of the object.  We would typically start a python interpreter, either from a UNIX command shell or from the IDLE interactive development environment, import one of our Python modules, and then create an object which could be used via the mouse, but could be modified from within the interpreter.   This process will be illustrated when we describe the different modules.

Because Python programs are scripts, they are easily changed and do not need to be compiled.  The REU participants were therefore able to easily change the programs to suit their individual purposes.  They were encouraged to do so, and they frequently did.

The flexibility and ease of use of the Python language is achieved at the expense of speed.  To compensate for this, it is easy to extend the language with modules written in a language, such as C, which is more directly tied to the computer hardware and therefore faster.  A good strategy, which we followed, is to write special-purpose computational primitives in C and embed them in Python extension modules.  This software package includes one such extension module written in C.

Information on downloading and installing the software can be found here.

Similarity transformations and fractal curves

Similarity transformations of the complex plane provide an excellent illustration of how mathematical objects can be represented by objects in an object-oriented programming language.  The class Similarity is defined in the simple python module simify.py.  After importing this module, the python interpreter can be used as a similarity calculator.  Similarities can be composed using the * operator, or they can act as functions of a complex variable.

>>> from chaos.simify import *
>>> x = Similarity(3, 2+1j)
>>> x
z -> 3z + (2+1j)
>>> y = Similarity(1, 1-2j)
>>> y
z -> 1z + (1-2j)
>>> x*y
z -> 3z + (5-5j)
>>> y*x
z -> 3z + (3-1j)
>>> x(3-3j)
(11-8j)

The module also contains a few simple functions that we used to iteratively generate pictures of fractal curves, such as Koch's snowflake, as well as Hilbert's space-filling curve.  (Of course the picture only shows the curve obtained after finitely many steps of the iterative construction.)

Koch's Snowflake Hilbert's space-filling curve

(Click on the images to view animations of the iterative constructions.)

The programs koch.py and hilbert.py can be used to generate these images.

Graphical analysis

Graphical analysis is a simple but powerful geometric technique for analyzing the dynamics of a real-valued function  f(x).  Picture the orbit of a point under iteration of f as being contained in the line  y=x .  So the orbit of  x  is represented by the set {(x,x), (f(x), f(x)),  ( f(f(x)),  f(f(x)) ),  ...  }.  Superimpose the graph of  f(x)  and the graph of the line  y=x  .  Given a point  (x,x)  on the line, here is a graphical method for finding the point   (f(x),  f(x)) .  First draw a vertical line through  (x,x),  and find its interrsection (x,f(x)) with the graph of f.  Then draw a horizontal line, and find its intersection  (f(x),  f(x))  with the line   y=x .  The diagram obtained by repeating this construction gives a very clear picture of the orbit.  We used this method to study the dynamics of real quadratic functions of the form f(x) = x2 + c  for different values of the parameter  c .

Graphical analysis is effective with pencil-and-paper , but it is even more effective with a computer.  The Python module graphalyze.py defines an object that performs graphical analysis on the computer screen.  Start your Python interpreter, create a Graphalyzer object, and  use the Graphalyzer's set() method to set various parameter values.

>>> from chaos.graphalyze import *
>>> G = Graphalyzer()
>>> G.set(c=-1.24,x_min=-2, x_max = 2)

You will then have a window like this on your screen:

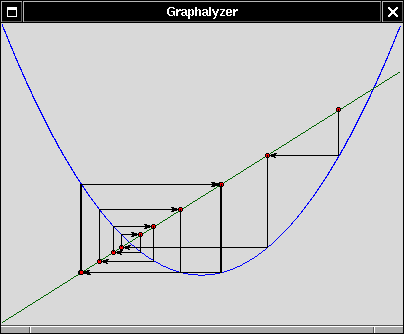
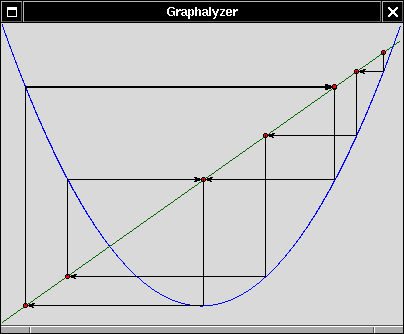
Graphalyzer window
 
A mouse click on the window starts the graphical analysis:

Graphalyzer window

The picture above shows an orbit that is attracted to the orbit of an attracting periodic point of period 2.  Below you see one which is attracted to the orbit of an attracting periodic point of period 3.

Graphalyzer window

Of course it is much harder to find repelling periodic orbits.  With some luck and a great deal of patience, some of the REU participants did manage to find some repelling periodic points by this graphical method.

Orbit diagrams

The graphical analysis of the family  f(x) = x2 + c makes it clear that the periods of the attracting periodic points vary in an interesting way as we vary c, and that the most interesting behavior takes place when c lies between -2 and .25.   An orbit diagram gives a way to understand this better by showing the attracting periodic points for all of the (interesting) values of c at once.   To generate an orbit diagram, we plot a large number of points of the orbit of 0 under  f(y) = y2 + c along the vertical line x=c.  We get a clearer picture if we throw away the first few orbit points, since it takes a few iterations before the points land close to an attracting periodic point.

A Python object for viewing orbit diagrams is defined in the module orbits.py .  To use it, start your Python interpreter, import the orbits module, and create an OrbitDiagram object:

>>> from chaos.orbits import *
>>> D = OrbitDiagram()

This will create a window on your screen which looks like this:

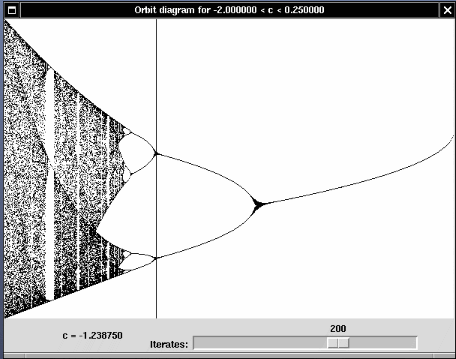
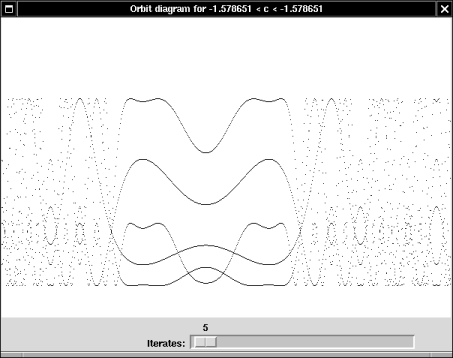
Orbit diagram window

The slider controls how many iterates are plotted on each vertical line, and the mouse controls the vertical line on the screen which corresponds to the c value printed at the lower left.  By clicking-and-dragging the mouse you can select a smaller interval of c values to study.  Clicking the right mouse button expands the size of the c interval by a factor of 2.

The vertical line in the picture above is located approximately at a  c value where period doubling occurs.  As c is decreased past this value the attracting periodic point with period 2 is replaced by an attracting periodic point of period 4.  One gets an intuitive understanding for the phenomenon of period doubling by experimenting with the OrbitDiagram.

One can also get some sense of what is happening in the dark colored chaotic regime by zooming in on a small c interval and plotting only a few iterates.  The picture below shows 5 iterates as c varies over a very small interval.  This small part of the orbit diagram seems to make a transition from relatively chaotic behavior to relatively stable behavior and back.

Orbit diagram window   

In our explorations we found that inside of an interval of c values where the dynamical system appears to be chaotic, by zooming in far enough one can find much smaller intervals of c values where the behavior seems to be stable.  We were led to the following problem.

Question: For the real dynamical system given by iterating f(x) = x2 + c, does the chaotic regime, where the critical orbit is not attracted to a periodic orbit,  form a Cantor set?

Complex dynamics - Julia sets and the Mandelbrot set

During the REU the software that we used for studying complex dynamics was developed in stages as we first stduied Julia sets and later the Mandelbrot set.  Here we provide a single program with everything rolled into one.  The Python module quaditerate.py defines a general Viewer class and two subclasses, Julia and Mandelbrot, for viewing the two types of sets.  We will need only the Mandelbrot class, since it creates instances of the Julia class as needed.

To use the program, start a Python interpreter, import the quaditerate module, and create a Mandelbrot object:

>>> from chaos.quaditerate import *
>>> M = Mandelbrot()

You should now have a window with a picture of the famous Mandelbrot set:

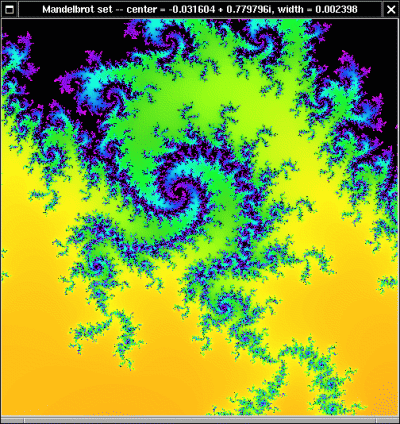
Mandelbrot window

Click and drag the mouse to zoom in.  (The click locates the center of the next view when zooming in.  Clicking the right mouse button zooms out.)

Mandelbrot window

The Mandelbrot set lies in the c-plane.  Clicking with the middle button opens a window with a picture of the filled Julia set associated to the c-value under the pointer.

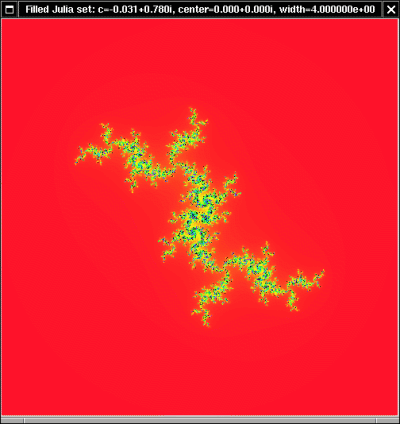
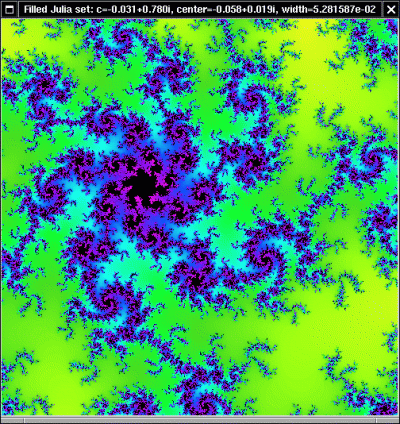
Julia window

Click and drag to zoom in on the filled Julia set, or use the right button to zoom out.

Julia window

Clicking the middle mouse button toggles between a picture of the filled Julia set and a picture of the Julia set, i.e. the boundary of the filled Julia set. An estimate of the box dimension of the Julia set is displayed when the Julia set is visible.  (We will say more about box dimension later.)

Julia window

A few words are in order to explain how to interpret these pictures.

We are studying the dynamical systems given by iterating the functions f(z) = z2 + c where z is a complex variable and  c is a complex parameter.  The Mandelbrot set is the set of values of c such that the orbit of 0 does not escape to infinity.  It is colored black in these pictures.  For values of c that are not in the Mandelbrot set the orbit of 0 does escape to infinity.  The color of a pixel corresponding to the number c is the first integer n  such that |fn(0)| > 2.  We know that the orbit of 0 escapes to infinity if and only if some iterate has absolute value greater than 2.  (In fact we only check 256 iterates, so some c values will be colored black even though they lie slightly outside the Mandelbrot set.)


For a fixed value of c, the filled Julia set FJc is the set of z values such that the orbit of z does not escape to infinity.
In our pictures of the filled Julia set the color of a pixel is black if the orbit of the corresponding z value does not escape from the circle of radius 2 after 256 iterates.  Otherwise the color represents the number of iterates before it does escape from the circle of radius 2 (and therefore escapes to infinity.)  The Julia set Jc  is the boundary of the filled Julia set, and is represented by the black pixels in the black-and-white pictures.

We studied the theorem that the Julia  set Jc is connected if c lies in the Mandelbrot set, and totally disconnected otherwise.  As c moves from 0 to a point outside the Mandelbrot set the Julia set changes shape, breaking up into "fractal dust" as c crosses the boundary of the Mandelbrot set.

Fractal dust

(Click on the image to see an animation of the Julia set breaking up into fractal dust.)

The program dust.py allows you to watch how the Julia set changes as c is varied.  To run the program start a Python interpreter, import dust.py and then call the function todust with the starting and ending values of c.

>>> from chaos.dust import *
>>> todust(-.5+0j, -1+1j)

Box dimension

 While the Julia sets Jc are all totally disconnected for values of c outside of the Mandelbrot set, they have different fractal dimensions.  We discussed various definitions of fractal dimension, which all agree for many types of sets. Using the similarity dimension it was easy to compute that Koch's snowflake has dimension  log 4 / log 3 = 1.261... . For computational purposes, however, the box dimension may be the most useful since the box dimension of a set can be estimated from a discretization of the set.

The box dimension of a bounded set X in the plane is defined as follows.  Consider a square grid on the plane where each box has sides of length r.  Let N(r)  be the number of these boxes that meet X.  Then the box dimension of X is the lim inf as r tends to 0 of the ratio -log N(r) / log r .

If we have a black-and-white computer image of X, where we are thinking of X being represented by the black pixels, then we can estimate the box dimension of X by covering the image with a grid in which each box is r pixels by r pixels.  If N(r) is the number of boxes of size r that contain black pixeks, then - log N(r) / log r is an approximation of the box dimension.  To estimate the limit as r tends to 0 we can maeasure - log N(r) for several values of r and then use least squares linear regression to fit a line to the data  (- log r1, log N(r1) ) , ... , (- log rk, log N(rk) ) .  The slope of the line is
then an estimate of the box dimension of the set X.

The Python module box.py implements this algorithm.  One can start with any image that has pixel values from 0 to 255.  The set X is the discrete boundary of the set of pixels with value less than T for some threshold value T between 0 and 255.  To use the program, start a Python interpreter,
import the box module and then create a Box object.  It must be initialized with the name of an image file and a threshold value:

>>> from chaos.box import *
>>> B = Box('koch.gif',1)

Here we are initializing our box object with the gif image of Koch's snowflake from the top of this web page.  We get two windows, one showing the black-and-white image of the boundary of the image, and one showing the least squares regression used to estimate the dimension:

Regression window
 Box dimension window

The estimated dimension of 1.275 is reassuringly close to the actual box dimension of Koch's snowflake, 1.261... .

Complex square roots

To understand why the Julia set Jc is totally disconnected when c lies outside of the Mandelbrot set we needed to understand the complex square root.  The Python module squirt.py helps to visualize the square root.  Think of an image as a function that assigns a color to each point w of the complex plane.  (Our image is probably a rectangle, but we can assume that each point outside the rectangle is colored black.) We can then define a new image as follows.  If z2=w then assign to the point z of the new image the same color as the point w of the old image.  The squirt module allows you to draw an image with the mouse or, for better entertainment value, to load an image from a file.  It then computes the new image as above.  The center of the image is taken to be the complex number 0, and the real and imaginary axes are superimposed on the picture.  The method Squirt.sqrt()  computes the new image as above.  Be patient -- the program is written entirely in Python and takes some time to run!

To use the program, start a Python interpreter, import the squirt module, and create a Squirt object.  Then call the sqrt method of the object:

>>> from chaos.squirt import *
>>> S = Squirt('w.gif')
>>> S.sqrt()

Here are the results:

w
 z2  = w


W image
 z image