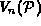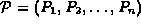Mixed volumes relate the volume of a polytope to the surface area of its
faces. This becomes apparent by the following recursive formula to
compute the mixed volume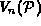 
of a tuple of polytopes
:
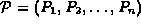where 
ranges over all normals on facets spanned by edges of the
polytopes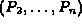 
. The function 
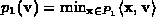is the support
function of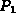 
. U is a unimodular transformation (
),
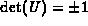with first row equal to 
, so that the arguments of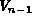 
live in
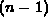-dimensional space.
By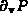 
we denote the face of P, of those points in P
for which the value of the support function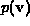 
is attained.
Bernshtein's proposed to use the homotopy
where c is the constant term of the first polynomial 
.
Applying (12) to a system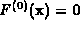 
with randomly chosen complex coefficients, Bernshtein proved that
all isolated solutions of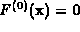 
can be obtained.
This solver runs in an analogue recursive way as formula (11).
Because formule (11) deals with the original polytope
configuration, we can get an indication whether the polytopes
are in generic position, i.e.: if for any direction 
, there exists
a component i, so that 
is a vertex.
The vectors computed in the elaboration of (11) provide potential
candidates showing that the system is not in generic position.
We now call this method implicit lifting, as a special instance of a lifting method to compute mixed volumes, a method we explain next.
