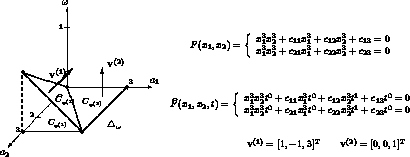
Figure 6: On the left the regular triangulation is pictured. The corresponding polynomial system and the induced homotopy are displayed at the right.
The dynamic lifting algorithm allows to construct subdivisions in an incremental fashion, iterated over the monomials in the systems. We start with only some monomials from every equation and gradually augment the current system with new monomials, extending the subdivision and the solution sets along the way, see [24]. Figure 6 illustrates this idea.

Figure 6: On the left the regular triangulation is pictured. The corresponding
polynomial system and the induced homotopy are displayed at the right.
Because we can bound the growth of the lifting values, the powers of the continuation parameter in the induced homotopy are as small as possible. In practice we have observed that dynamic lifting produces homotopies whose solution paths are better conditioned than by random lifting.
The dynamic lifting algorithm offers an efficient implementation of
the so-called Cayley trick.
The Cayley trick reduces the mixed-volume computation to the
computation of the volume of a larger,  -dimensional polytope,
where r equals the number of different polytopes in the tuple
-dimensional polytope,
where r equals the number of different polytopes in the tuple  .
In practice, it turns out that this trick is efficient when the
system is semimixed, i.e., when r is small.
.
In practice, it turns out that this trick is efficient when the
system is semimixed, i.e., when r is small.