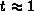 .
Here we may have to deal with paths converging to singular solutions
and with paths running to infinity, as
.
Here we may have to deal with paths converging to singular solutions
and with paths running to infinity, as 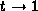 .
In this stage, we have to track the paths more carefully.
.
In this stage, we have to track the paths more carefully.
PoCo supports two different types of homotopies. The user can give either an artificial-parameter homotopy, by explicitly giving a start system, or a natural-parameter homotopy, in the form of a polynomial system with one unknown more than the number of equations. In both cases a list of start solutions must be provided.
The tracing of the solution paths is organized in two
stages. During the first stage we have t < 1.
No singularities are likely to occur in this stage.
Moreover, we are not interested in the exact solutions for t<1.
So we can afford ourselves to track the paths more loosely.
The second stage is at the end of each path, when 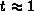 .
Here we may have to deal with paths converging to singular solutions
and with paths running to infinity, as
.
Here we may have to deal with paths converging to singular solutions
and with paths running to infinity, as 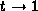 .
In this stage, we have to track the paths more carefully.
.
In this stage, we have to track the paths more carefully.
The solution paths are not likely to turn back as the continuation
parameter t increases.
Therefore, instead of pseudo arc-length, only increment-and-fix predictor
corrector methods have been implemented.
This means that after each increase of t, t remains fixed
while correcting the solution  .
There are four different predictor methods available.
They are listed in Table 2, with a short description.
.
There are four different predictor methods available.
They are listed in Table 2, with a short description.
The complex predictor for t is based on an idea of Drexler,
see [6], who proposed to take t in complex space when
singularities during continuation occurred.
The differences between secant and tangent predictor are illustrated
in Figure 7.
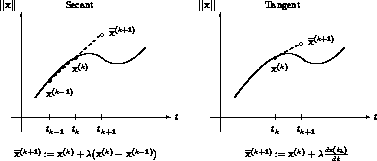
Figure 7: The secant and tangent predictor with  as step length.
as step length.
In Figure 7, we see that the tangent predictor is able to follow the solution path more accurately. This justifies the extra work, such as computing derivatives and solving a linear system.
We distinguish four different sets of parameters:
 and for t. The number of steps along a path is bounded.
The distance from the target to the beginning of the end game can be
adjusted.
Finally, the automatic mechanism of re-computing clustered paths is
controlled by the maximum number of re-runs.
and for t. The number of steps along a path is bounded.
The distance from the target to the beginning of the end game can be
adjusted.
Finally, the automatic mechanism of re-computing clustered paths is
controlled by the maximum number of re-runs.
Distinguishing path failures either due to singular solutions or to solutions at infinity has been a hard task until recently. Taking Bernshtein's second theorem into account, by means of an inexpensive side-calculation the directions of diverging paths can be approximated up to a sufficient level of accuracy. The path directions of diverging paths yield the outer normals to the faces of the Newton polytopes, which cause the deficiency. This feature of PoCo provides a certificate of deficiency from diverging solution paths.
There are several output levels available to put the data processed during continuation on a log file. The user can choose to see only the solutions at the end of the path or to have all intermediate solutions on file. Furthermore, information about the performance of predictor and corrector can be delivered at all intermediate steps. The output file of PoCo could in this way become an input file to routines to visualize the solution paths.