



Next: Programming in Ada
Up: Polynomial Homotopy Continuation: a
Previous: Vali: Validation of
Our progress on solving has always been motivated by the poor performance
of the existing technology on practical examples.
Because benchmarks are mainly used for comparison, most systems are
derived from practical applications, cited in the literature.
In Table 3 we present an overview of a part of our benchmark.
The explicit description of the systems, omitted to save space, can be
found in [18].
Every line presents an entry of the database and collects the main
characteristics.
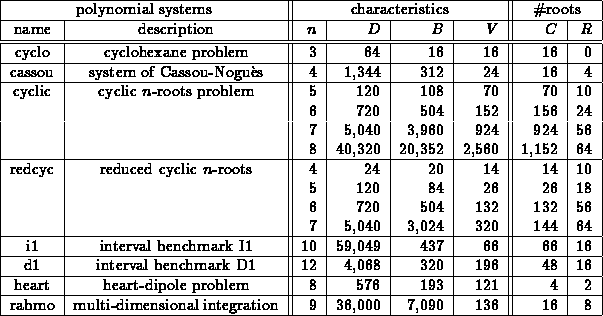
Table 3: Characteristics of polynomial systems in benchmark. Besides the
name and a description we list the dimension n, total degree D, Bézout
bound B and mixed volume V. Furthermore, the number of isolated roots
in complex (C) and in real (R) space are given.
We see the dramatic gap between various root counts.
Furthermore we have to point at the importance of the problem formulation:
reduced cyclic n-roots represents the cyclic 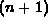 -roots problem.
This reformulation allows to solve the problem about n times faster.
-roots problem.
This reformulation allows to solve the problem about n times faster.
Root counts determine the practical performance of the homotopies.
In this sense, these mathematical figures give a more honest and timeless
impression than actual execution times.
Jan Verschelde
Thu Nov 21 10:50:01 MET 1996

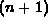 -roots problem.
This reformulation allows to solve the problem about n times faster.
-roots problem.
This reformulation allows to solve the problem about n times faster.