Monitoring the path tracker

 

the condition of the homotopy: 

This global parameter can be used to tune the parameters according to the general expectancy of how difficult the solution paths will be. Low values of this parameter lead to a loose path tracking, whereas higher values tighten up the path-following.

number of paths tracked simultaneously: 

In simultaneous path-following , the same discretization for the values of the continuation parameter is used for a number of paths. Clustering of solution paths is checked during continuation for the number of paths that are followed simultaneously. In sequential path-following , i.e., when this parameter equals one, the step sizes are adjusted according to the difficulty of the current path being followed. In this case, a difficult path does not slow down the continuation for the other ones.

maximum number of steps along a path: 

This parameter bounds the amount of work along a solution path. Continuation for the path being followed stops when the number of steps exceeds this threshold value.

distance from target to start end game: 

Tracking solution paths is organized in two stages. As t<1, no singularities are likely to occur and paths can be tracked more loosely. When 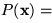$t \approx 1$, paths may converge to singular solutions  or diverge to infinity , so they have to be tracked more carefully. This distance marks the switch towards the second stage, that is the so-called end game .

order of extrapolator in end game: 

The direction of a diverging solution path provides a normal to a face of the system that certificates the deficiency. In this polyhedral end game , extrapolation  is used to determine winding numbers . When the order of the extrapolator equals zero, then the polyhedral end game is turned off.

maximum number of re-runs:  

Solution paths may be clustered at the end of the continuation. If the number of re-runs is higher than one, then clustered solution paths are re-computed by following the paths more closely. Setting this value to zero turns off this facility.