



Next: Path closeness
Up: Polynomial Continuation
Previous: Monitoring the path tracker
- predictor type:
- We distinguish between predictors for the solution vector
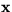 and the continuation parameter t.
The secant predictor
for
and the continuation parameter t.
The secant predictor
for 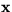 is based on linear extrapolation,
whereas the tangent predictor
uses the Jacobian matrix to extrapolate.
For t, three different predictors are provided.
The real predictor
simply augments t with the step size.
The complex predictor
takes values in the complex plane to circumvent
values of t for which the corresponding system is badly conditioned.
The geometric predictor
generates values for t so that the distances
to the target value behave like a geometric series.
The latter predictor is useful in a polyhedral end game.
is based on linear extrapolation,
whereas the tangent predictor
uses the Jacobian matrix to extrapolate.
For t, three different predictors are provided.
The real predictor
simply augments t with the step size.
The complex predictor
takes values in the complex plane to circumvent
values of t for which the corresponding system is badly conditioned.
The geometric predictor
generates values for t so that the distances
to the target value behave like a geometric series.
The latter predictor is useful in a polyhedral end game.
- minimum step size:
- This is a lower bound on the step size for the continuation parameter.
Continuation for the path being followed stops when a required
reduction of the step size yields a step length that is lower
than the minimum step size.
- maximum step size:
- This is an upper bound on the step size for the continuation parameter.
An expansion of the step size that yields a step length that is
larger than this threshold sets the step size to this threshold.
- reduction factor for step size:
- When the corrector does not manage to reach the required accuracy
within the allowed number of iterations, the step size will be
reduced by multiplication with the reduction factor.
- expansion factor for step size:
- When the corrector has reached the required accuracy within the
allowed number of iterations, for a number of consecutive times
higher than the expansion threshold, the step size will be enlarged
by multiplication by the expansion factor.
- expansion threshold:
- Before enlarging the step size along a path, the number of consecutive
successful steps must pass the expansion threshold.
A step is successful when the corrector manages to reach the required
accuracy within the allowed number of iterations.
At the end of the path, this threshold bounds the number of consecutive
equal guesses of the winding number m before the polyhedral end game
can modify it.




Next: Path closeness
Up: Polynomial Continuation
Previous: Monitoring the path tracker
Jan Verschelde
3/7/1999