Welcome to MCS 275

The goal of this second introductory programming course is to explore the capabilities offered Python and to practice some useful problem solving techniques such as backtracking.

Version 3.6 of Python will be used. On occasion, we mention some important differences with version 2.

In this lecture we cover the writing of an algorithm from an input/output statement; followed by the coding of the algorithm in a Python script.

Programming in Python

We distinguish between programming in the small and programming in the large.

As a scripting language, Python offers many advantages for small programs:

  1. As an interpreted language, the immediate execution lends itself well to rapid prototyping. Python offers dynamic typing and automatic garbage collection which frees the user from the perils of memory allocation and deallocation.
  2. Although not as efficient as compiled code, Python is open to extension modules for C code. Computationally intensive tasks can therefore remain in compiled code and invoked from Python.

For writing large programs, Python offers two benefits:

  1. Python is an object oriented language. Object Oriented Programming (OOP) aims to organize the code to promote reuse, change, and scalability.

  2. Python comes with batteries included. The Open Source revolution has given us LAMP, where

    • L stands for Linux, the operating system,
    • A is for Apache, the web server,
    • M is for MySQL, the database, and
    • P is for Python, the scripting language.

    Python glues many important software components.

Factorization in Primes

As an example problem to introduce programming, weconsider the factorization in primes.

A prime has only two divisors: 1 and itself. Every natural number can be factored as a unique product of primes.

The input/output statement of our problem is listed below:

\[\begin{split}\begin{array}{rcl} input & : & \mbox{a natural number } n \\ output & : & \mbox{a list of primes } [p_1,p_2,\ldots,p_k], \\ & & n = p_1 \times p_2 \times \cdots \times p_k \end{array}\end{split}\]

After we understand the problem statement, a first step in solving the problem is to think about simplifications. Are there related, easier problems we can solve? In this case, there is. We can list all divisors of a number. The input/output statement of this simpler problem is listed below:

\[\begin{split}\begin{array}{rcl} input & : & \mbox{a natural number } n \\ output & : & \mbox{a list of all nontrivial divisors of } n \end{array}\end{split}\]

In the problem statement, 1 and \(n\) are trivial divisors. Let us look at the easier problem first. But first, note that we care about clarity and correctness, efficiency concerns come second (if at all).

Ingredients in a first algorithm:

  1. \(d\) divides \(n\) if \(n~ \% ~d\) == 0 (zero remainder)
  2. enumerate all candidate divisors, for \(d\) ranging between 2 and \(n-1\), for \(d\) in range(2, n)
  3. append divisor \(d\) to a list L using L.append (\(d\))

Now we will put the ingredients into a recipe. A flowchart representation of the algorithm is in Fig. 1.

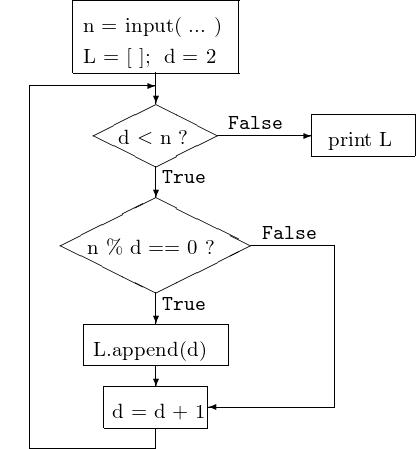
_images/figflowenumdiv.png

Fig. 1 Flowchart of the algorithm to enumerate all nontrivial divisors.

The Python code in the file enumdivs.py is in its entirety listed below.

# MCS 275 L-1 Mon 9 Jan 2017 : enumdivs.py
"""
enumerate all nontrivial divisors of a number
"""
NBR = int(input('give a number : '))
FACTORS = []
DIVISOR = 1
for DIVISOR in range(2, NBR):
    if NBR % DIVISOR == 0:
        FACTORS.append(DIVISOR)
print('nontrivial divisors of %d :' % NBR, FACTORS)

Running the script at the command prompt $ can go as follows:

$ python enumdivs.py
give a number : 24
nontrivial divisors of 24 : [2, 3, 4, 6, 8, 12]

Even as the code in enumdivs.py is quite short, there are a few interesting observations to make:

  • The input() command returns a string. With int() we cast the string into an integer.
  • The command range(2, NBR) produces the list [2,3,..,NBR-1].
  • All code in the same for or if must be preceded by same number of spaces.
  • There are three different occurrences of %:
    1. NBR % DIVISOR: remainder after division by DIVISOR,
    2. %d: formatting code for decimal output,
    3. %: format conversion operator in print.
  • The append is a method for the list data type.
  • Long numbers will take a long time.

Now go back to the original problem, the factorization of a number in primes.

We first formulate a solution in words and list the ingredients in a first algorithm:

  1. We enumerate all candidate divisors, starting at 2.
  2. When we find a divisor \(d\) of \(n\), we continue with the quotient \(q\), so we assign \(n = q\).
  3. \((q,r) = \mbox{\tt divmod}(n,d)\) computes quotient \(q\) and remainder \(r\) of the division of \(n\) by \(d\).
  4. All divisors are appended to a list.

The flowchart for an algorithm to compute the prime factorization of a natural number is in Fig. 2.

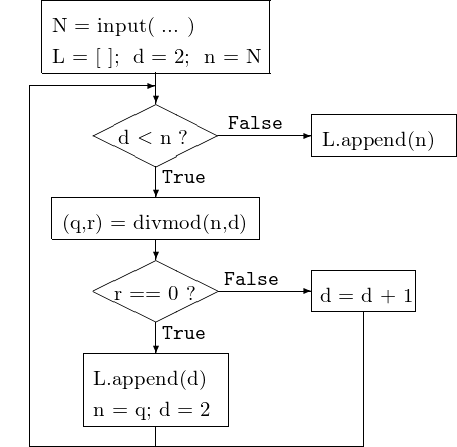
_images/figflowfacprimes.png

Fig. 2 Flowchart to factor a natural number in primes.

The code in the script facnum.py is listed below.

from functools import reduce
NBR = int(input('give a natural number n : '))
FACTORS = []
DIVISOR = 2
WORK = NBR
while DIVISOR < WORK:
    (QUOT, REST) = divmod(WORK, DIVISOR)
    if REST == 0:
        FACTORS.append(DIVISOR)
        (WORK, DIVISOR) = (QUOT, 2)
    else:
        DIVISOR = DIVISOR + 1
FACTORS.append(WORK)
print('factors of ' + str(NBR) + ' :', FACTORS)
PRD = reduce(lambda x, y: x*y, FACTORS)
print('product of factors :', PRD)

In Python 2, the function reduce() is a built-in function which offers support for functional programming. In Python 3, reduce() now belongs to the module functools which must be imported explicitly before usage. The statement

PRD = reduce(lambda x,y: x*y , FACTORS)

computes the product

\[p = \prod_{p_i \in L} p_i = p_1 \times p_2 \times \cdots \times p_k.\]

The anonymous function lambda x,y: x*y is applied to the list FACTORS reducing the list FACTORS to the product of all its elements.

Exercises

  1. Use facnum.py to verify that 2017 is a prime number. What is the next year (following 2017) that is a prime number?
  2. Make enumdivs.py more efficient by examining only \(\sqrt{n}\) candidate divisors.
  3. Relate the number of \(n \% d\) operations in enumdivs.py to the number of decimal places of \(n\). If we add one more decimal place to the input \(n\), how many more operations does enumdivs.py do?
  4. Improve the efficiency of facnum.py also by taking fewer candidate divisors as in exercise 2 above.
  5. Verify the correctness of facnum.py by an exhaustive enumeration of all numbers \(n\) within the range \(1, \ldots, m\), where \(m\) is given by the user.
  6. Analyze the running time of facnum.py experimentally by trying various input numbers. For which numbers does facnum.py take the longest time? Which numbers are easiest?