Extending Python

Because Python is interpreted, its execution efficiency for computationally extensive problems is often inadequate. This is the case for the factorization in primes problem of the first lecture.

We can extend Python with a module which exported compiled C code which runs much faster.

Timing Programs

We take the same Python script as in the previous lecture to factor a natural number in primes. The only modification – in preparation for the C code – is that the output is written to a string, instead of to a list.

The input-output specification is stated below:

\[\begin{split}\begin{array}{rcl} input & : & \mbox{a natural number } n \\ output & : & \mbox{a string } n = p_1 ~ p_2 ~ \cdots ~ p_k, k > 0 \\ & & \mbox{where } n = p_1 \times p_2 \times \cdots \times p_k \\ & & \mbox{and every } p_i \mbox{ is prime, } i=1,2\ldots,k. \end{array}\end{split}\]

As an example, considering a run of the script at the command prompt $:

$ python facnums.py
give a natural number n : 121121
121121 = 7 11 11 11 13
$

Writing the output to a string can be viewed as delaying the print statements during the computation. If n is a number, then

print('%d = ', n)

is equivalent to

s = '%d = ' % n
print(s)

Observe the following:

• The '%d' is a format string and the % following the string is the conversion operator.
• We can update the string s via s = s + ' %d' % n and postpone the printing of s till the end of the program.

The flowchart for the algorithm is in Fig. 3.

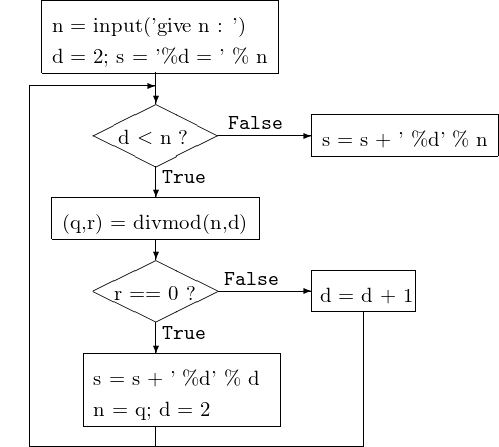
Fig. 3 Factoring a natural number in primes, writing the output to a string.

The modified script facnums.py is below:

"""
factor a number into product of primes,
writing the result to a string
"""
n = eval(input('give a natural number n : '))
d = 2; s = '%d =' % n
while(d < n):
    (q,r) = divmod(n,d)
    if(r == 0):
        s = s + ' %d' % d
        n = q; d = 2
    else:
        d = d + 1
s = s + ' %d' % n
print(s)

The easiest way to time programs (at least on Unix like operating systems) is to use the time command. Because slow typers may take a long time to enter the input, we direct the input so the input is read from file. In the example below, we use the input file input, which contains the single number 121121.

$ time python3 facnums.py < input
give a natural number n : 121121 = 7 11 11 11 13

real    0m0.039s
user    0m0.027s
sys     0m0.009s

It takes 39 milliseconds total, of which 27 milliseconds are spent on the user program, there are 9 milliseconds of time spent by the system.

For prime numbers, the program takes a long time, consider running the Python script versus a C program on the prime number on 1000000007. The runs are performed on a MacBook Pro, of early 2015, which has a 3.1 GHz Intel Core i7.

$ time python3 facnums.py < input_prime
give a natural number n : 1000000007 = 1000000007

real    8m13.203s
user    7m58.106s
sys     0m 3.166s

The C program facnum0.c is compiled with gcc as gcc -o /tmp/facnum0 facnum0.c and we run it on the same input:

$ time /tmp/facnum0 < input_prime
give a natural number n : 1000000007 = 1000000007

real    0m2.848s
user    0m2.786s
sys     0m0.015s

The C program is 173 times faster than Python!

Writing a C program

Starting from the Python script, we will develop an equivalent C program.

Every C program typically starts with the inclusion of one or several header files before the definition of the main function. Unlike the dynamic typing mechanism in Python, the types of the variables in C must be declared explicitly. The start of the C program facnum0.c is as follows:

/* L-2 MCS 275 : facnum0.c */

#include <stdio.h>

int main ( void )
{
   int n,d,r;

   printf("give a natural number n : ");
   scanf("%d",&n);

   printf("%d =",n);

Observe the following:

• The typing in C is static: n, d, r are of type int.
• The header file stdio.h contains the functions printf and scanf to respectively write and read.
• The symbol &n is the address of the variable n.
• The C code is block oriented. The beginning of each block is marked with the opening curly brace { while } marks the end of the block.

To introduce the control structures in C, we put the equivalent C statement next to the Python ones.

d = 2;                 | d = 2
while(d < n)           | while(d < n):
{                      |
   r = n % d;          |    r = n % d
   if(r == 0)          |    if(r == 0):
   {                   |
      printf(" %d",d); |       print(' %d' % d)
      n = n/d;         |       n = n//d
      d = 2;           |       d = 2
   }                   |
   else                |    else:
      d = d + 1;       |       d = d + 1
}                      |
printf(" %d\n",n);     | print(' %d\n' % n)

return 0;

The return 0; is the typical last statement in the main function of a C program. The returned 0 indicates to the operating system the normal termination of the program.

The prime factors computed by the C program will be passed to Python in a string – delaying the printing. Therefore, the C code will print to a string.

The statement

printf("%d = ",n)

is then equivalent to

char s[80]; /* 80 characters for result */
sprintf(s,"%d =",n); /* print to s */

Adding a factor d to the result s:

char f[10]; /* 10 characters for factor */
sprintf(f," %d",d);
strcat(s,f); /* string concatenation */

The printing to a string instead of immediately to screen is a first step to make a library version of the code to export the C code to Python. The next step is to wrap the computations in a function.

The rewriting of code, wrapping code into a functions for reuse or extensions, is a practice called refactoring. Instead of one main function, we have a function factor which isolates the computations. The input and output are then still handled by the main function.

#include <stdio.h>
#include <string.h>

int factor ( int n, char *s );
/* writes the prime factors of n to the string s */

int main ( void )
{
   int n;
   char s[80]; /* string for result */

   printf("give a natural number n : ");
   scanf("%d",&n);
   factor(n,s);
   printf("%s",s); /* print result */

   return 0;
}

Before the definition of the main function, we formulate the prototype of the function. The prototype list the name and the arguments of the function. Once the prototype is defined, the function can be called in the code that follows the prototype.

After the definition of the main function, we define the code for the function factor.

int factor ( int n, char *s )
{
   int d,r;
   char f[10]; /* string for factor */
   sprintf(s,"%d =",n);
   d = 2;
   while(d < n)
   {
      r = n % d;
      if(r == 0)
      {
         sprintf(f," %d",d);
         strcat(s,f);
         n = n/d; d = 2;
      }
      else
         d = d + 1;
   }
   sprintf(f," %d\n",n);
   strcat(s,f);
   return 0;
}

Call by Value and Call by Reference

In the C function prototype

int factor ( int n, char *s );

there are two parameters: n and s. The * before the s indicates that the function expects an address to a character. This address defines the beginning of the sequence of characters in the string s. In factor, we pass the parameter s as call by reference. There is no * before the parameter n and then we say that the parameter n is passed as call by value.

The main differences between call by value and call be reference are the following:

• call by value: The value of the variable is passed to the function. The value is not changed by the function.
• call by reference: Instead of the value, the address, or a reference to the variable is passed to the function. This address defines the location of the value in memory. The function may change the value of the parameeter that is passed by a call by reference.

In Python, we can also work with references to values. Consider the following session:

>>> a = 3; b = a
>>> (a,b)
(3, 3)
>>> a = 4
>>> (a,b)
(4, 3)

In the first line, b is assigned to a and thus gets the same value. We say that a and b both refer to the integer 3. When we assign 4 to a, the value a refers to changes, but b still refers to 3. Suppose that we wanted b to change as well, because we want b to be just another name for the same value a refers to. With lists we can accomplish this.

>>> a = [3]; b = a
>>> (a,b)
([3], [3])
>>> a[0] = 4
>>> (a,b)
([4], [4])

One way to interpret the statement a = [3] is that a refers to the list [ ] which contains as first element a[0] and the variable a[0] refers to the integer 3. With the assignment b = a, the name``b`` refers to the same list [ ] referred to by a, which contains as its first element a[0]. When we change a[0] we change the first element of the list b refers to. Thus with lists, we have that b is just another name for the same object the name a refers to.

In a Python function, call it also factor, we can achieve the same call by reference effect by given a list as argument. Consider the schematic of a function definition:

def factor ( nbr, result ):
    result.append(..)

Whatever we do to the list result, e.g.: append some object, the result of this operation will remain to the caller of the function.

Extending Python

The goal is to use the C code from a Python session. The C code will be in a module NumFac.

>>> import NumFac
>>> dir(NumFac)
['__doc__', '__file__', '__name__', 'factor', 'test']
>>> from NumFac import test, factor
>>> test()
give a natural number n : 121121
121121 = 7 11 11 11 13
>>> s = factor(121121,'')
>>> s
'121121 = 7 11 11 11 13\n'
>>> s.split(' ')
['121121', '=', '7', '11', '11', '11', '13\n']

After the split, the factors are in a list.

We will define the code for the extension and the instructions to build the shared object NumFac.so step by step:

1. Locate on your computer, for the correct version of Python, the location of the header file Python.h.

   The location of this header file Python.h needs to be passed to the compiler. Add the definition of the location in the makefile, with the proper gcc compiler instruction.

2. The main function in the C program will be converted into a test function which also will be exported by the shared object. This interactive test function takes no input arguments.

3. We wrap the function factor in a Python function.

4. The registration table defines the functions in the shared object that are exported to Python.

5. At the end of the file, we define the initialization of the module.

In the first step, we append to the file with the C code:

#include "Python.h"

In the makefile, we need to define the location of Python.h:

PYTHON3=/Library/Frameworks/Python.framework/Versions/3.6/include/python3.6m

NumFac.so:
        gcc -dynamiclib -undefined dynamic_lookup \
            -o NumFac.so -I$(PYTHON3) numfac.c

Typing make NumFac.so at the command prompt in a Terminal window will then make the shared object NumFac.so. Note that in the makefile, the gcc is preceded by one tab.

In the second step, we define an interactive test function. It is good practice to keep the main program as an interactive test program:

static PyObject *NumFac_test ( PyObject *self, PyObject *args )
{
   test();
   return (PyObject*)Py_BuildValue("");
}

While the function test takes no input arguments and does not return anything, the function factor does. In the third step, we define the wrapping of the function factor.

static PyObject *NumFac_factor ( PyObject *self, PyObject *args )
{
   PyObject *result;
   int n;
   char s[80];
   if(!PyArg_ParseTuple(args,"is",&n,&s)) return NULL;
   factor(n,s);
   result = (PyObject*)Py_BuildValue("s",s);
   return result;
}

In the fourth step, we define the registration table. The registration table contains the documentation strings for the functions the module exports:

static PyMethodDef NumFacMethods[] =
{
   { "factor" , NumFac_factor , METH_VARARGS,
     "factor a natural number into primes" } ,
   { "test" , NumFac_test , METH_VARARGS,
     "interactive test on prime factoring" } ,
   { NULL , NULL, 0, NULL } ,
};

The documentation strings show when the user does help().

The fifth and last step deals with the module initialization. At the end of the file, we initialize the module:

static struct PyModuleDef NumFacModule = {
   PyModuleDef_HEAD_INIT,
   "NumFac",
   "prime number factorization",
   -1,
   NumFacMethods
};

PyMODINIT_FUNC
PyInit_NumFac()
{
   return PyModule_Create(&NumFacModule);
}

After the five steps, we compile and install the module. To check whether the extension module is still valid C code, we compile as gcc -c numfac.c To create a shareable object (file with extension .so), we create a script setup.py:

from distutils.core import setup, Extension

# for using numfac.c :

MOD = 'NumFac'
setup(name=MOD,ext_modules=[Extension(MOD, sources=['numfac.c'])])

and do python3 setup.py build Instead of python3 setup.py install, do cp build/lib*/NumFac.so . (copy the shareable object to the current directory).

Exercises

1. Take the script enumdivs.py from Lecture 1 and write a corresponding C program: enumdivs.c. Write the factors to screen instead of into a list.

2. Modify the enumdivs.c from the previous exercise so that the factors are written into a string.

3. Use the modified enumdivs.c from the previous exercise to build a Python extension EnumDivs.

4. Take a Python function to compute the greatest common divisor of two natural numbers a and b:

   s = 'gcd(%d,%d) = ' % (a,b)
   r = a % b
   while r != 0:
      a = b
      b = r
      r = a % b
   print s + '%d' % b
   

   Build a Python extension from equivalent C code.