Solving Puzzles

We will apply recursive backtracking to solve puzzles. A classical problem is the search for a path in a maze. We solve this problem first without a GUI and then with a GUI. A variation of this problem is percolation. We end defining the problem of a sliding puzzle.

Finding a Path in a Maze

Our goal is to find a path in a maze (or labyrinth). In our application of recursive backtracking, we use a list of lists to represent the maze. In the second stage with develop a GUI with Tkinter.

There are two stages in the program:

1. We define the maze, modifying a random distribution of blocked squares. This stage is shown in Fig. 30.
2. We find a path in the maze, as shown in Fig. 31.

We develop our solution in two parts. First with a plain text interface to understand the essential concepts. With a GUI, we obtain a more enjoyable program.

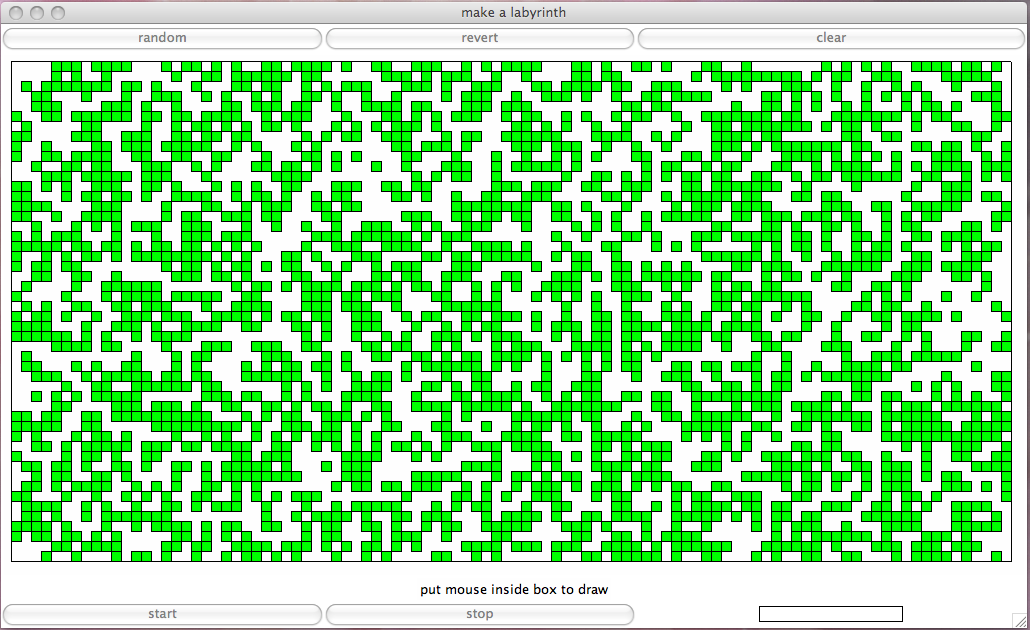
Fig. 30 Defining a path in a maze.

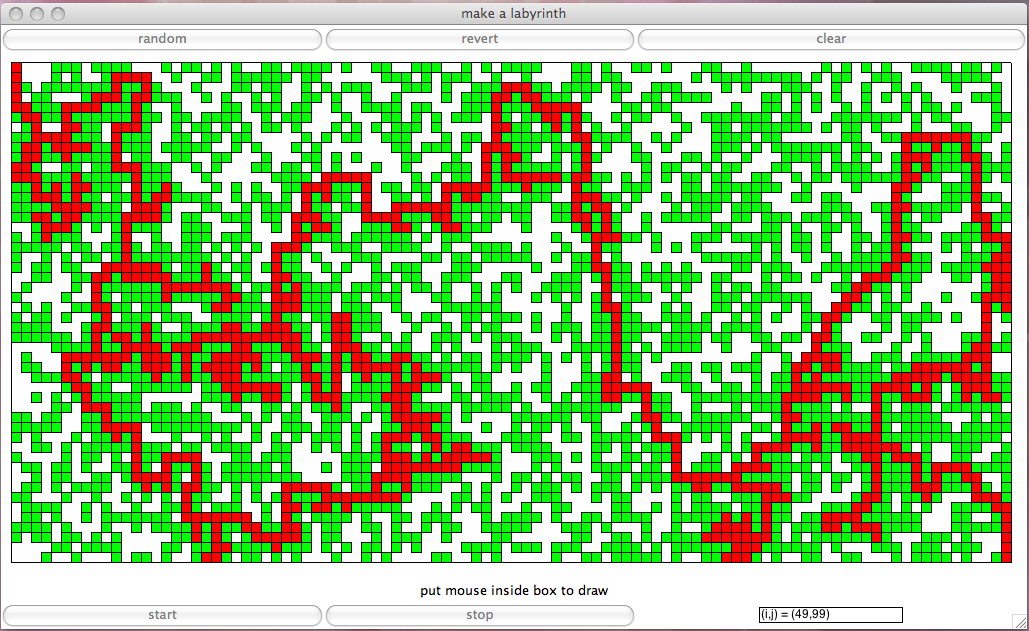
Fig. 31 Finding a path in a maze.

To represent the maze, we use a list of lists of integer entries. Each square [i][j] of the maze can have three types of values:

1. -1 indicates the square is blocked.
2. 0 indicates the square is free and is not visited on any path.
3. k indicates the square is visited as the k-th square in a path.

By marking the visited squares we never walk along the same path and the walk terminates. In a maze with \(n\) rows and \(m\) columns,

• a path starts at square \([0][0]\); and
• \([n-1][m-1]\) is the destination of the path.

Code to make a random maze is defined by the function below.

def random_maze(rows, cols):
    """
    Returns a list of lists, as many lists as the value
    of rows, and every list has as many elements as the
    value of cols.  A zero indicates a free position,
    occupied positions are marked by -1.
    Positions [0][0] and [rows-1][cols-1] are free.
    """
    from random import randint
    maze = []
    for _ in range(rows):
        row = [randint(-1, 0) for _ in range(cols)]
        maze.append(row)
    maze[0][0] = 0
    maze[rows-1][cols-1] = 0
    return maze

A randomly generated maze is often unlikely to allow for a path from [0][0] to [rows-1][cols-1]]. With an interactive function, listed below, the user can turn blocked squares into free ones to make a path.

def make_maze(rows, cols):
    """
    Generates a random maze of the dimensions specified
    by rows and cols.  The user can make adjustments.
    """
    maze = random_maze(rows, cols)
    while True:
        show_maze(maze)
        row = int(input('to change, give row index : '))
        if row < 0:
            break
        col = int(input('to change, give column index : '))
        if col < 0:
            break
        maze[row][col] = (-1 if maze[row][col] == 0 else 0)
    return maze

In the development of a recursive solution, defined by a function search_path(), we first determine its parameters.

The input are the four elements in tuple (M, i, j, k):

• M represents the maze, as a list of lists;
• i and j are indices to respectively a row and a column of M where M[i][j] is a free position;
• k is the counter for the square M[i][j] visited on the path.

Therefore, M[i][j] will be the k-th square visited on the path.

The output are two elements in the tuple (M, b):

• M records the visited squares, marked with increasing numbers;
• b is True if the destination is reached and is False if stepping on M[i][j] did not lead to the destination.

Upon return from the call (M, b) = search_path(M, i, j, k), the search will continue to the next free square if b is False, or else it will stop.

If the search does not stop, where to go next? There are four directions to go:

\[\begin{split}\begin{array}{c|c|c} & (i-1,j) & \\ \hline (i,j-1) & (i,j) & (i,j+1) \\ \hline & (i+1,j) & \end{array}\end{split}\]

subject to the following conditions:

• go to row \(i-1\), only if \(i > 0\),
• go to row \(i+1\), only if \(i < n-1\), where \(n\) equals the number of rows,
• go to column \(j-1\), only if \(j > 0\),
• go to column \(j+1\), only if \(j < m-1\), where \(m\) equals the number of columns,
• of course, the square must be free and not visited before.

The base case is given in the code below:

def search_path(maze, i, j, k):
    """
    Given a maze and a current free position [i][j],
    marks the position in the maze with the value of k.
    Searches a path to the position [rows-1][columns-1]
    where rows is the number of rows in maze and
    where columns is the number of elements in all rows.
    Visited tiles are marked with increasing numbers.
    Returns the maze and a boolean indicating the arrival.
    """
    maze[i][j] = k
    if i == len(maze)-1 and j == len(maze[i]) - 1:
        return (maze, True)
    else:

For the backtracking part, we have to explore all four directions (west, east, north, and south of the current square) subject to the conditions formulated above. The code for search_path then continues.

# backtracking in the general case of search_path
    arrived = False
    if i < len(maze)-1:
        if maze[i+1][j] == 0:
            (maze, arrived) = search_path(maze, i+1, j, k+1)
    if not arrived and j < len(maze[i])-1:
        if maze[i][j+1] == 0:
            (maze, arrived) = search_path(maze, i, j+1, k+1)
    if not arrived and i > 0:
        if maze[i-1][j] == 0:
            (maze, arrived) = search_path(maze, i-1, j, k+1)
    if not arrived and j > 0:
        if maze[i][j-1] == 0:
            (maze, arrived) = search_path(maze, i, j-1, k+1)
    return (maze, arrived)

Handling Mouse Events

To develop the GUI for this puzzle, we have to consider how to deal with mouse input.

Often the amount of data we generate is too huge for an orderly in a classical terminal window. Much more data can be stored in an image on canvas and via the mouse we may interact with the data. In Fig. 32 is a simple GUI to illustrate the filling of squares on canvas with mouse clicks.

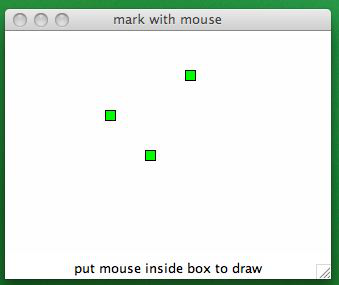
Fig. 32 Filling squares on canvas with mouse clicks.

We view the canvas as a grid of squares. The constructor of the class FillingSquares defines the setup of the GUI.

from tkinter import Tk, Label, Canvas, StringVar
from random import randint

class FillingSquares(object):
    """
    Filling squares on canvas with mouse clicks.
    """
    def __init__(self, wdw, r, c):
        """
        The mouse is bound to the canvas,
        with given rows and columns.
        A label displays mouse position.
        """
        wdw.title("mark with mouse")
        self.mag = 10   # magnification factor
        self.rows = r   # number of rows on canvas
        self.cols = c   # number of columns on canvas
        self.cnv = Canvas(wdw,\
            width=self.mag*self.cols+2*self.mag,\
            height = self.mag*self.rows+2*self.mag,\
            bg='white')
        self.cnv.grid(row=1, column=0, columnspan=3)
        # to display mouse position :
        self.MousePosition = StringVar()
        self.MousePosition.set("put mouse inside box to draw")
        self.PositionLabel = Label(wdw, \
            textvariable=self.MousePosition)
            self.PositionLabel.grid(row=2, column=0, columnspan=3)
        # bind mouse events
        self.BindMouseEvents()
        # storing which squares are filled
        self.filled = []
        for i in range(r):
            self.filled.append([0 for _ in range(c)])

The binding of the mouse events is done in the constructor – notice the call sell.BindMouseEvents() – and defined in the method below.

def BindMouseEvents(self):
    """
    Binds mouse events to the canvas.
    """
    self.cnv.bind("<Button-1>", self.ButtonPressed)
    self.cnv.bind("<ButtonRelease-1>", self.ButtonReleased)
    self.cnv.bind("<Enter>", self.EnteredWindow)
    self.cnv.bind("<Leave>", self.ExitedWindow)
    self.cnv.bind("<B1-Motion>", self.MouseDragged)

The methods ButtonPressed, ButtonReleased, EnteredWindow, ExitedWindow, and MouseDragged are activated by the mouse. The methods are defined below.

def ButtonPressed(self, event):
    """
    Display the coordinates of the button pressed.
    """
    self.MousePosition.set("currently at [ " + \
        str(event.x) + ", " + str(event.y) + " ]" +\
        " release to fill, or drag")

The message label guides the user of the GUI.

def ButtonReleased(self, event):
    """
    Displays the coordinates of button released.
    """
    self.MousePosition.set("drawn at [ " + \
        str(event.x) + ", " + str(event.y) + " ]" + \
        " redo to clear")
    self.DrawRectangle(event.x,event.y)

The DrawRectangle defines the action of the GUI. The other methods below make use only of the message label to give feedback to the user.

def EnteredWindow(self, event):
    """
    Displays the message that mouse entered window.
    """
    self.MousePosition.set("press mouse to give coordinates")

def ExitedWindow(self, event):
    """
    Displays the message that mouse exited window.
    """
    self.MousePosition.set("put mouse inside box to draw")

def MouseDragged(self, event):
    """
    Display the coordinates of a moving mouse.
    """
    self.MousePosition.set("dragging at [ " + \
        str(event.x) + ", " + str(event.y) + " ]" + \
        " release to draw")

This simple example suffices to continue the development of the GUi to visualize the search of a path in a maze.

A GUI to Search a Path in a Maze

In defining the GUI, we start with listing the data attributes. The list of lists that represents the maze is the main data attribute of the GUI. The layout of the GUI is defined by the following widgets:

• A canvas to draw the maze.
• Buttons make the maze, called random, revert, and clear. The random button fills squares at random on canvas, while revert inverts the state of each square, filling empty squares and emptying filled squares. The button clear wipes the canvas clean.
• Buttons start and stop, to start and stop the animation.
• An entry widget shows the current position in the maze.

With the mouse, the user can free up squares to define a path through the maze.

The button Random activates the method:

def RandomFill(self):
    """
    Fills the canvas with boxes placed at random.
    """
    for i in range(0, len(self.filled)):
        for j in range(0, len(self.filled[i])):
            name = '('+str(i)+','+str(j)+')'
    ...

Observe the following:

• The self.filled is a list of lists.
• Every square at row i and column j has a unique name: (i,j).

The complete definition of the initial definition of the maze is below.

def RandomFill(self):
    """
    Fills the canvas with boxes placed at random.
    """
    for i in range(0, len(self.filled)):
        for j in range(0, len(self.filled[i])):
            name = '('+str(i)+','+str(j)+')'
            if randint(0, 1) == 1:
                x0 = self.mag+i*self.mag
                y0 = self.mag+j*self.mag
                x1 = x0 + self.mag; y1 = y0 + self.mag
                self.cnv.create_rectangle(y0,x0,y1,x1, \
                    fill="green",tags=name)
                self.filled[i][j] = -1
            else:
                self.cnv.delete(name)
                self.filled[i][j] = 0

Now we arrive at the definition of the animation of the search. Recall the definition of the function Search(M,i,j,k), where M represented the maze. For the GUI, we have the data attribute filled to define the maze. The GUI exports the method animate applied to self, with parameters i, j, and k. The return of animate is a boolean to indicate if the destination was reached. Because the maze is a data attribute of the GUI, animate does not return a matrix.

def animate(self,i,j,k):
    """
    starts the search for a path
    """
    self.filled[i][j] = k
    self.ent.delete(0, END)
    self.ent.insert(INSERT, \
        '(i,j) = ('+str(i)+','+str(j)+')')
    x0 = (i+1)*self.mag; y0 = (j+1)*self.mag
    x1 = (i+2)*self.mag; y1 = (j+2)*self.mag
    self.cnv.create_rectangle \
        (y0,x0,y1,x1,fill="red",tags='dot')
    self.cnv.after(self.delay)
    self.cnv.update()
    if self.go:
        if i == len(self.filled) - 1 \
            and j == len(self.filled[i]) - 1:
            return True  # found the end
    else:
        b = False
        if self.go and i < len(self.filled)-1:
            if self.filled[i+1][j] == 0 and self.go:
                b = self.animate(i+1, j, k+1)
        if not b and self.go:
            if j < len(self.filled[i])-1:
                if self.filled[i][j+1] == 0 and self.go:
                    b = self.animate(i, j+1, k+1)
        if not b and self.go and i > 0:
            if self.filled[i-1][j] == 0 and self.go:
                b = self.animate(i-1, j, k+1)
        if not b and self.go and j > 0:
            if self.filled[i][j-1] == 0 and self.go:
                b = self.animate(i, j-1, k+1)
        return b

Percolation and Sliding Puzzles

A variation on search for a path in a maze is the percolation problem, illustrated in Fig. 33. There is percolation if there is a path starting at an open square at the top and ending at an open square at the bottom. Both configurations in Fig. 33 percolate, but only the one on the left percolates vertically.

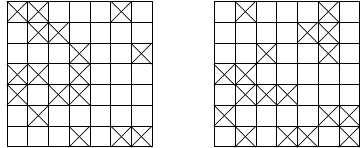
Fig. 33 Empty squares admit flow, crosses block the flow.

Simulations like these provide a starting point to study porous materials, leading into the subject of percolation theory.

An example of a sliding puzzle is shown in Fig. 34.

Fig. 34 The goal of the puzzle is to sort the squares by sliding.

The rules of the sliding puzzle are as follows. Given is a n-by-n board of sliding pieces. There is one open space where adjacent pieces may slide into. Each piece has a unique number. This number determines its right place on the board. The goal of the sliding puzzle is to slide each piece to its right spot on the board.

The GUI contains several elements:

• buttons to start, scramble, unscramble, and clear;
• a canvas widget to display the sliding puzzle;
• a list of lists stores the puzzle data;
• the scramble/unscramble buttons are animations; and
• mouse events allow user to solve the puzzle.

What defines a move? When piece \((i,j)\) moves to its adjacent open spot.

A puzzle with n rows and m columns is solved if piece at \((i,j)\) has number \(i \times (n-1) + j + 1\), for all pieces in the puzzle. The function solve will first check whether the values for the pieces match their position. If so, return True. This check is the base case.

In the general case, we generate recursive calls. For all pieces p adjacent to the open spot, run the following statements in a loop:

1. Slide p to the open spot.
2. Do the recursive call b = solve().
3. Test the return value: if b: break and the puzzle is solved.

Exercises

1. Modify the Search function to solve the percolation problem. Test if your modification works.
2. Adjust the GUI for finding a path through a maze to the percolation problem.
3. Instead of changing the length of the bars with scales in project one, explore how to change the length by allowing the user to drag the joints with the mouse.
4. Add a solve button to sliding_puzzle.py and write code for solving the puzzle.
5. Compare the difficulty of solving the sliding puzzles with finding a path in a maze. Which one is harder and why?
6. Suppose a graph is represented by a list of lists A of zeroes and ones. If there is an edge from node i to j, then \(A[i][j] = 1\), otherwise \(A[i][j] = 0\). Write a Python function to find a path between any two nodes.