Enumeration and Backtracking

Enumeration and backtracking are exhaustive problem solving methods, applying recursive algorithms. The exhaustiveness often leads to exponential time. Greedy algorithms and heuristic methods may prune the search space and give satisfactory practical performance.

Enumerating Bit Combinations

Consider the automatic generation of truth tables. For example, we can simplify expressions via De Morgan’s law:

\[{{\tt not~ (( not~x )~or~( not~y ))} ~=~ {\tt x~and~y}}\]

A Truth Table proves De Morgan’s law:

\[\begin{split}\begin{array}{cc|ccc|cc} {\tt x} & {\tt y} & {\rm (1)} & {\rm (2)} & {\rm (3)} & {\rm (4)} & {\rm (5)} \\ \hline 0 & 0 & 1 & 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 1 & 1 \end{array}\end{split}\]

where in the table above, we made the following abbreviations: \(0 = {\tt False}\), \(1 = {\tt True}\), \({\rm (1)} = {\tt not~x}\), \({\rm (2)} = {\tt not~y}\), \({\rm (3)} = {\rm (1)} {\tt ~or~} {\rm (2)}\), \({\rm (4)} = {\tt not~} {\rm (3)}\), \({\rm (5)} = {\tt x~and~y}\). The proof of the law follows from the last two columns in the table being equal to each other.

In writing all bit combinations, we will develop the script enumbits.py. Its running is illustrated below.

$ python3 enumbits.py
Give number of bits : 3
[0, 0, 0]
[0, 0, 1]
[0, 1, 0]
[0, 1, 1]
[1, 0, 0]
[1, 0, 1]
[1, 1, 0]
[1, 1, 1]

Observe the pattern in this enumeration. The lists are list in lexicographic order, as words in a dictinary.

In the recursive computation of all bit combinations, we view the bit sequences as the leaves of a binary tree. The internal nodes of the tree are only partially filled in, as in Fig. 29.

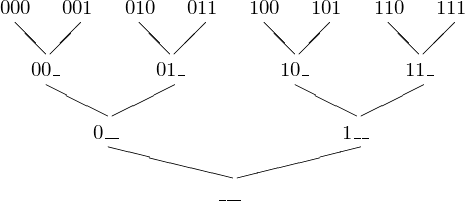
Fig. 29 A binary tree to list all bit combinations.

The tree grows from its root to the leaves:

• Every leave is a print statement (base case).
• Every internal node is a recursive function call.

Let’s define a recursive function enumbits, to compute a combinations of \(n\) bits. Two parameters suffice for this function:

• bits is a list which serves as the accumulating parameter; and
• k points to the current position in the list.

Initially, k == 0 and bits has space for \(n\) objects.

in the base case when k == len(bits), then we execute print bits.

In general, for k < len(bits):

1. bits[k] = 0, call enumbits for k+1
2. bits[k] = 1, call enumbits for k+1

The main program is below:

def main():
    """
    Prompts the user for number of bits
    and initializes the list.
    """
    nbr = int(input('Give the number of bits : '))
    lst = [0 for _ in range(nbr)]
    enumbits(0, lst)

The prototype for the recursive function is

def enumbits(k, bits):
    """
    Writes all bit combinations of len(bits),
    starting at the k-th position.
    """

The definition of the parameters and their functionality counts often for more than half of the solution. The complete definition of the function comes next.

def enumbits(k, bits):
    """
    Writes all bit combinations of len(bits),
    starting at the k-th position.
    """
    if k >= len(bits):
        print(bits)
    else:
        bits[k] = 0
        enumbits(k+1, bits)
        bits[k] = 1
        enumbits(k+1, bits)

The first application is the computation of truth tables. We exploit Python’s dynamic typing, as in the following session:

>>> e = "not x or not y"
>>> x = True
>>> y = False
>>> eval(e)
True

Logical expressions as strings delays their evaluation. We can apply eval only if all variables in an expression have values.

An extension of the bit enumeration is for problems when there are more than two alternatives: Then the number N of alternatives is an extra parameter. In the general case, the loop for k in range(N) enumerate all choices.

An illustration of combining many alternatives, consider a problem you may encounter when solving a crossword puzzle.

Enumerate all three letter words: begin{enumerate} item starting with c, s, or v; item with one vowel in the middle; and item ending in d, t, or w. end{enumerate} This problem is solved by the product of three lists:

csv = ['c', 's', 'v']
vowels = ['a', 'e', 'i', 'o', 'u']
dtw = ['d', 't', 'w']

The number of plausible words equals \(3 \times 5 \times 3 = 45\).

Our recursive function enumwords has 3 parameters:

1. letters is a list of lists to choose from;
2. k is the index to current list; and
3. accu is a string accumulating the word.

Recall that adding a character c to a string s is done simply as s + c.

Initially, we have k == 0 and accu == ''. The recursive algorithm then compares k to len(letters):

• If k == len(letter), then do print accu. This is the base case.
• Otherwise, for all characters letter in letters[k], call enumwords with k+1 and accu + letter.

The main function is as follows:

def main():
    """
    enumerates letter combinations
    """
    csv = ['c', 's', 'v']
    vowels = ['a', 'e', 'i', 'o', 'u']
    dtw = ['d', 't', 'w']
    let = [csv, vowels, dtw]
    enumwords(0, let, '')

where the function enumwords is defined below:

def enumwords(k, letters, accu):
    """
    Starting with the k-th list in letters,
    adds letters to the current string accu.
    """
    if k >= len(letters):
        print(accu)
    else:
        for letter in letters[k]:
            enumwords(k+1, letters, accu+letter)

Another extension to the recursive enumeriation is to add a stopping condition. Consider a session where we ask the user whether to continue or not.

$ python3 enumwstop.py
the word is "cad" continue ? (y/n) y
the word is "cat" continue ? (y/n) y
the word is "caw" continue ? (y/n) y
the word is "ced" continue ? (y/n) y
the word is "cet" continue ? (y/n) n

The changes to enumwords are summarized in the following items.

• The base case calls an interactive function.
• The return value of enumwords is a boolean: to continue or not.
• In the general case, if a call to enumwords returns False, then we break out of the loop.

The question in the interactive session is encapsulated in the function ask_to_continue().

def ask_to_continue(word):
    """
    Shows the string word and then asks
    the user to continue or not.
    """
    qst = 'the word is \"' + word + '\"'
    qst = qst + ' continue ? (y/n) '
    ans = input(qst)
    return ans == 'y'

Then the changed function enumwords is below.

def enumwords(k, letters, accu):
    """
    Starting with the k-th list in letters,
    adds letters to the current string accu,
    returns a boolean: to continue or not.
    """
    if k >= len(letters):
        return ask_to_continue(accu)
    else:
        for letter in letters[k]:
            cont = enumwords(k+1, letters, accu+letter)
            if not cont:
                break
        return cont

Backtracking

To introduce backtracking, consider the knapsack problem. A traveler selects objects to put in a knapsack. The problem statement is the following:

\[\begin{split}\begin{array}{rcl} input & : & \mbox{a list of values } V, \mbox{a lower bound } L, \mbox{and an upper bound } U \\ output & : & \mbox{all selections } S \subseteq V: \sum_{s \in S} \in [L, U] \end{array}\end{split}\]

In an extended version the input is a list of weights. The upper bound is for the sum of weights. The lower bound is for the sum of values.

A restricted problem is the subset sum problem. Find all sums of numbers in a given list that match a given value.

Running the script knapsack.py could go as follows.

$ python3 knapsack.py
give number of objects : 5
give a list of 5 values : [2.1, 1.8, 3.2, 4.1, 0.8]
lower bound on sum : 3
upper bound on sum : 5
V([0, 1, 4]) = 2.10 + 1.80 + 0.80 = 4.70
V([0, 1]) = 2.10 + 1.80 = 3.90
V([1, 2]) = 1.80 + 3.20 = 5.00
V([2, 4]) = 3.20 + 0.80 = 4.00
V([2]) = 3.20 = 3.20
V([3, 4]) = 4.10 + 0.80 = 4.90
V([3]) = 4.10 = 4.10

In designing a recursive algorithm, we first define the parameters.

• The recursive function knapsack takes on input the list of values V and the bounds on the sum.
• The parameter k is the index of the current object being considered for inclusion in the knapsack.

In the base case, we have k == len(V). If the sum(V) is within bounds, then V is printed.

In the general case, for k < len(V), consider adding object k

• only if its value V[k] plus the current sum does not exceed the upper bound.
• Also call for k+1 without adding it.

Finally, we have two accumulating parameters: The current selection and the list of the values of the current selection.

In the definition of the recursive function knapsack observe the specification in the documentation string.

def knapsack(things, low, upp, k, sel, val):
    """
    Shows all selections sel of things whose sum
    of values in val: low <= sum(val) <= upp.
    Input parameters:
    things : a list of values;
    low : lower bound on sum;
    upp : upper bound on sum;
    k : index to the current thing.
    Accumulating parameters:
    sel : stores selection of things;
          if selected i-th thing in things,
          then sel[i] == 1, else sel[i] == 0;
    val : values of the selected things.
    Initialize sel and val both to [], k to 0.
    """
    if k >= len(things):
        if low <= sum(val) <= upp:
            write(sel, val)
    if k < len(things):
        if sum(val) + things[k] <= upp:
            sel.append(k)
            val.append(things[k])
            knapsack(things, low, upp, k+1, sel, val)
            del sel[len(sel)-1]
            del val[len(val)-1]
        knapsack(things, low, upp, k+1, sel, val)

The helper function write() called in the base case of knapsack is defined below.

def write(sel, val):
    """
    Does formatted printing in knapsack,
    for the selection sel and values val.
    """
    result = 'V(' + str(sel) + ') = '
    for i in range(0, len(val)):
        if i > 0:
            result = result + ' + '
        result = result + '%.2f' % val[i]
    result = result + ' = ' + '%.2f' % sum(val)
    print(result)

We end with the code for the function main().

def main():
    """
    Prompts user for the number of objects
    asks for the list of their values,
    a lower and an upper bound on the sum.
    """
    from ast import literal_eval
    nbr = int(input('give number of objects : '))
    qst = 'give a list of %d values : ' % nbr
    vals = literal_eval(input(qst))
    low = float(input('lower bound on sum : '))
    upp = float(input('upper bound on sum : '))
    knapsack(vals, low, upp, 0, [], [])

if __name__ == "__main__":
    main()

Exercises

1. Use the enumeration of all bit combinations in a script to verify using a truth table whether two logical expressions are equivalent.
2. Write code to enumerate all sublists of a given list.
3. Modify the code for the recursive function knapsack with an interactive stopping condition.
4. Let the script for the knapsack problem also take on input the weights of the objects. Prompt the user for an additional list of weights and use the upper bound for the total weight of the selected objects.
5. In chess, a queen can attack all squares that run horizontally, vertically, and diagonally starting at the queen’s position. On an 8-by-8 chess board, compute in how many ways you can put 8 queens so they do not attack each other.