Recursion versus Iteration¶
The Towers of Hanoi¶
The Towers of Hanoi is the name of an ancient mathematical puzzle.
The input is a number of disks on one pile. All disks have a different size. No larger disk sits above a smaller disk. There are two other empty piles. The input is shown at the left of Fig. 24.

Fig. 24 The towers of Hanoi: input on the left, output on the right.
The output is shown at the right of Fig. 24. The task is to move the disks from the first pile to the second,
- Move one disk at a time.
- Never place a larger disk on a smaller one, you may use the third pile as a buffer.
A recursive solution assumes we know how to move a stack with one disk less. This solution is sketched in Fig. 25.
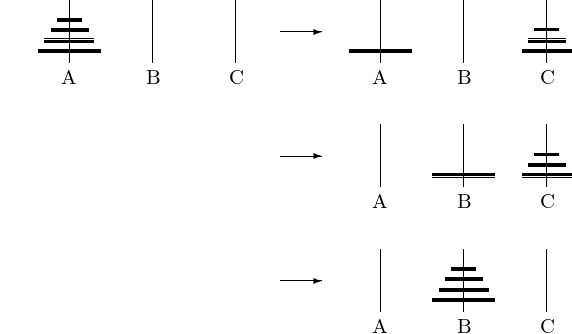
Fig. 25 A recursive solution to the towers of Hanoi problem.
A recursive algorithm runs through the following rules:
Base case: move one disk from A to B.
To move \(n\) disks from A to B:
Move \(n-1\) disks from A to C using B as auxiliary pile, see Fig. 26.
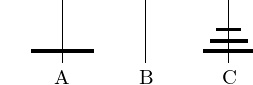
Fig. 26 Moving \(n-1\) disks from A to C using C as auxiliary pile.
Move the \(n\)-th disk from A to B, see Fig. 27.
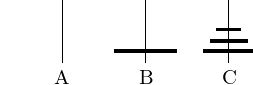
Fig. 27 Moving the \(n\)-th disk from A to B.
Move \(n-1\) disks from C to B, using A as auxiliary pile, see Fig. 28.
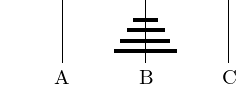
Fig. 28 Moving \(n-1\) disks from C to B, using A as auxiliary pile.
In our Python solution, we use a stack. In a stack, we remove only the top element (we pop) and add only at the top (we push). The session below illustrates the use of a list as a stack. Consider a pile of 4 disks of decreasing size, represented by the first 4 consecutive positive natural numbers:
>>> A = [x for x in range(1, 5)]
>>> A
[1, 2, 3, 4]
To remove the top element, we do
>>> A.pop(0)
1
>>> A
[2, 3, 4]
To put an element on top, we do
>>> A.insert(0,1)
[1, 2, 3, 4]
Below we formulate a recursive Python function to solve the towers of Hanoi problem.
def hanoi(nbr, apl, bpl, cpl):
"""
Moves nbr disks from apl to bpl, cpl is auxiliary.
"""
if nbr == 1:
# move disk from apl to bpl
bpl.insert(0, apl.pop(0))
else:
# move nbr-1 disks from apl to cpl, using bpl
hanoi(nbr-1, apl, cpl, bpl)
# move nbr-th disk from apl to bpl
bpl.insert(0, apl.pop(0))
# move nbr-1 disks from cpl to bpl, using apl
hanoi(nbr-1, cpl, bpl, apl)
The main function to interactively test the function hanoi
is next:
def main():
"""
Prompts for the number of disks,
initializes the piles, and
then calls the hanoi function.
"""
nbr = int(input('Give the number of disks :'))
apl = [x for x in range(nbr)]
bpl = []
cpl = []
print('A =', apl, 'B =', bpl, 'C =', cpl)
hanoi(nbr, apl, bpl, cpl)
print('A =', apl, 'B =', bpl, 'C =', cpl)
To experience the exponential complexity, we will trace the execution, adding extra print statements. A run with the extended solution is below.
$ python hanoi.py
Give number of disks : 4
at start : A = [1, 2, 3, 4] B = [] C = []
move 1, n = 1 : A = [2, 3, 4] C = [1] B = []
move 2, n = 2 : A = [3, 4] B = [2] C = [1]
move 3, n = 1 : C = [] B = [1, 2] A = [3, 4]
move 4, n = 3 : A = [4] C = [3] B = [1, 2]
move 5, n = 1 : B = [2] A = [1, 4] C = [3]
move 6, n = 2 : B = [] C = [2, 3] A = [1, 4]
move 7, n = 1 : A = [4] C = [1, 2, 3] B = []
move 8, n = 4 : A = [] B = [4] C = [1, 2, 3]
move 9, n = 1 : C = [2, 3] B = [1, 4] A = []
move 10, n = 2 : C = [3] A = [2] B = [1, 4]
move 11, n = 1 : B = [4] A = [1, 2] C = [3]
move 12, n = 3 : C = [] B = [3, 4] A = [1, 2]
move 13, n = 1 : A = [2] C = [1] B = [3, 4]
move 14, n = 2 : A = [] B = [2, 3, 4] C = [1]
move 15, n = 1 : C = [] B = [1, 2, 3, 4] A = []
In the output above, the number of spaces before the move counter
equals the depth of the tree of recursive calls.
In the extended version with the print statements, we have to change the representation of the piles. A simple list to represent a pile no longer suffices. The roles of the piles shift. Each pile is a 2-tuple:
- The name of the pile comes first. The name is a string.
- The second iterm is a list of numbers.
Writing a pile is then one single format conversion:
>>> pile = ('A', [1, 2, 3])
>>> '%s = %s' % pile
'A = [1, 2, 3]'
The writing of the piles is implemented in the function below.
def write_piles(pre, apl, bpl, cpl):
"""
Writes the contents of the piles apl, bpl,
and cpl, after writing the string pre.
Every pile is a 2-tuple: the name
of the pile and a list of numbers.
"""
sapl = '%s = %s' % apl
sbpl = '%s = %s' % bpl
scpl = '%s = %s' % cpl
print(pre, sapl, sbpl, scpl)
When we write the state of each pile, at each move, we like to see the recursion depth. The recursion depth is represented by the number of spaces.
def write(k, move, nbr, apl, bpl, cpl):
"""
Writes the contents of piles apl, bpl, cpl,
preceded by k spaces, writing the move
and the number of disks nbr.
"""
pre = k*' '
pre += 'move %d, n = %d :' % (move, nbr)
write_piles(pre, apl, bpl, cpl)
The third modification concerns the counting of the moves. In addition to the number of disks and the tuple representations of the piles, we need:
- a counter for the depth of the recursion, and
- a counter for the number of moves.
The function hanoi below has those two counters in its arguments.
def hanoi(nbr, apl, bpl, cpl, k, move):
"""
Moves nbr disks from apl to bpl, cpl is auxiliary.
The recursion depth is counted by k,
move counts the number of moves.
Writes the state of the piles after each move.
Returns the number of moves.
"""
Then then new main function is the following.
def main():
"""
Prompts user for the number of disks,
initializes the stacks and calls hanoi.
"""
nbr = int(input('Give number of disks : '))
apl = ('A', list(range(1, nbr+1)))
bpl = ('B', [])
cpl = ('C', [])
write_piles('at start :', apl, bpl, cpl)
cnt = hanoi(nbr, apl, bpl, cpl, 0, 0)
print('number of moves :', cnt)
write_piles(' at end :', apl, bpl, cpl)
The definition of the extended function hanoi is below.
def hanoi(nbr, apl, bpl, cpl, k, move):
"""
Moves nbr disks from apl to bpl, cpl is auxiliary.
The recursion depth is counted by k,
move counts the number of moves.
Writes the state of the piles after each move.
Returns the number of moves.
"""
if nbr == 1:
# move disk from A to B
bpl[1].insert(0, apl[1].pop(0))
write(k, move+1, nbr, apl, bpl, cpl)
return move+1
else:
# move nbr-1 disks from A to C, B is auxiliary
move = hanoi(nbr-1, apl, cpl, bpl, k+1, move)
# move nbr-th disk from A to B
bpl[1].insert(0, apl[1].pop(0))
write(k, move+1, nbr, apl, bpl, cpl)
# move nbr-1 disks from C to B, A is auxiliary
move = hanoi(nbr-1, cpl, bpl, apl, k+1, move+1)
return move
To solve a puzzle with 1 disk, we need 1 move. For 2 disks, 3 moves are needed. For 3 disks, we need 7 moves. In the example run of the extended versio of the code, we saw that 15 moves are needed for a puzzle with 4 disks. How many moves do we need to solve a puzzle with \(n\) disks?
Let \(T(n)\) count number of moves for \(n\) disks:
We find the general formula for :math:T(n)
by solving the recurrence relation:
The problem of the towers of Hanoi has an exponential complexity in its input size \(n\). The complexity is an intrinsic properly of a problem. No matter what algorithm we apply to solve this problem, its run time will always be proportional to its complexity.
The Fibonacci Numbers¶
The \(n\)-th Fibonacci number \(F_n\) is defined as
There are two base cases in the recursive solution,
implemented by the function fibonacci, listed below.
def fibonacci(nbr):
"""
Returns the nbr-th Fibonacci number.
"""
if nbr == 0:
return 0
elif nbr == 1:
return 1
else:
return fibonacci(nbr-1) + fibonacci(nbr-2)
Consider the tree of function calls, as shown below for the computation of \(F_5\).
$ python3 fibonacci.py
Give n : 5
F(5) = F(4) + F(3)
F(4) = F(3) + F(2)
F(3) = F(2) + F(1)
F(2) = F(1) + F(0)
F(1) = 1
F(0) = 0
F(1) = 1
F(2) = F(1) + F(0)
F(1) = 1
F(0) = 0
F(3) = F(2) + F(1)
F(2) = F(1) + F(0)
F(1) = 1
F(0) = 0
F(1) = 1
F(5) = 5
number of calls : 25
To compute the number 5,
we executed 25 function calls.
The code to trace the execution is below.
How many additions did we perform?
Is this number of addition optimal?
def fibotrace(nbr, k, cnt):
"""
Returns (f, cnt) where f is the nbr-th Fibonacci
number and cnt the number of function calls.
Prints execution trace using the control parameter k.
"""
outs = k*' ' + 'F(%d) = ' % nbr
if nbr == 0:
print(outs + '0')
return (0, cnt)
elif nbr == 1:
print(outs + '1')
return (1, cnt)
else:
print(outs + 'F(%d) + F(%d)' % (nbr-1, nbr-2))
(fb1, cnt1) = fibotrace(nbr-1, k+1, cnt+1)
(fb2, cnt2) = fibotrace(nbr-2, k+1, cnt+1)
return (fb1+fb2, cnt1+cnt2)
Consider the formulation of an iterative algorithm to compute the Fibonacci numbers. To compute \(F_n\), we execute \(n\) steps. In each step we add two numbers: the previous one to the previous to the previous one.
def iterfib(nbr):
"""
Iterative algorithm for nbr-th Fibonacci number.
"""
if nbr == 0:
return 0
else:
(first, second) = (0, 1)
for _ in range(2, nbr+1):
(first, second) = (second, first + second)
return second
Observe how code gets shorter with tuple assignment.
Although the iterative formulation is simple enough, it is different from the definition, which always makes the verification of the correctness harder. There is an alternative implementation, which uses the original recursive definition, without sacrificing efficiency. This alternative is provided by memoization.
Memoization¶
The towers of Hanoi problem is hard no matter what algorithm is used, because its complexity is exponential. The first recursive computation of the Fibonacci numbers took long, its cost is exponential. The computation of the \(n\)-th Fibonacci numbers requires \(n-1\) additions, so its complexity is linear.
If the number of function calls exceeds the size of the results, it may be better use an iterative formulation. Using a stack to store the function calls, every recursive program can be transformed into an iterative one.
As an alternative to an iterative solution,
we introduce memoization using the Fibonacci numbers.
What if we store the results of
previous function calls in a Python dictionary?
A dictionary is a set of key:value pairs.
We use the dictionary as follows:
- The
keywill store the value of the parameter. - The
valuestores the value of the result.
Using the dictionary D:
- Every call with
nstarts with a lookup: isn in D? - If
n in D, thenreturn D[n]. - Otherwise, store the result
RwithD[n] = R.
We exploit a feature of Python: we can store data in a function call. To an argument of a function we assign a dictionary:
def storecalls(nbr, calls={}):
"""
Stores the value of nbr in the dictionary calls.
Each time we print the address of calls
and all values stored in calls.
The length of the dictionary records the number
of times the function is called.
"""
print('calls =', calls, 'with id =', id(calls))
calls[len(calls)] = nbr
The id() function returns the identity of an object.
CPython returns the memory address of the object.
An example of running storecalls is in the session below.
$ python storecalls.py
give a number (0 to exit) : 3
calls = {} with id = 4300915016
give a number (0 to exit) : 4
calls = {0: 3} with id = 4300915016
give a number (0 to exit) : 8
calls = {0: 3, 1: 4} with id = 4300915016
give a number (0 to exit) : 2
calls = {0: 3, 1: 4, 2: 8} with id = 4300915016
...
What just happened?
- At the first call to the function, the arguments of the
function are evaluated. With
calls = { }, an empty dictionary is created and placed somewhere in memory. - At each following call, the same memory address is used.
Using the address (returned in the output of id()),
we can obtain the value of the object stored at the location
defined by the address.
This process is called dereferencing an address.
Importing the function storecalls
from the module storecalls:
>>> from storecalls import storecalls
>>> storecalls(3)
calls = {} with id = 4303043528
>>> storecalls(8)
calls = {0: 3} with id = 4303043528
>>> from ctypes import cast, py_object
>>> cast(4303043528, py_object).value
{0: 3, 1: 8}
In CPython, id() returns the address.
With cast we can dereference the address: given the address,
we obtain the value of the object stored at that address.
Applying this feature from Python to memoizing the function to compute the Fibonacci numbers is implemented below.
def memfib(nbr, calls={}):
"""
Returns the nbr-th Fibonacci number, using calls to
memoize the values computed in previous calls.
"""
if nbr in calls: # first check the dictionary
return calls[nbr]
else: # compute the value recursively
if nbr == 0:
result = 0 # first base case
elif nbr == 1:
result = 1 # second base case
else:
result = memfib(nbr-1) + memfib(nbr-2)
calls[nbr] = result # store in the dictionary
return result
Observe that the control structure corresponds to the mathematical definition of the Fibonacci numbers.
Now that we can compute large Fibonacci numbers fast, we run into another limitation. The recursion limit is the maximum depth of the Python interpreter stack. This limit prevents infinite recursion.
>>> from sys import getrecursionlimit
>>> getrecursionlimit()
1000
We can set the maximum depth of the Python interpreter stack:
>>> from sys import setrecursionlimit
>>> setrecursionlimit(2000)
>>> getrecursionlimit()
2000
We need this to compute large Fibonacci numbers.
The new function main() is listed below.
from sys import setrecursionlimit
def main():
"""
Prompts the user for a number n,
and computes the n-th Fibonacci number.
"""
nbr = int(input('Give a number : '))
setrecursionlimit(nbr+3)
fib = memfib(nbr)
print('The %d-th Fibonacci number is %d' % (nbr, fib))
if __name__ == "__main__":
main()
Exercises¶
- We define the Harmonic numbers \(H_n\) as \(H_1 = 1\) and \(H_{n} = H_{n-1} + 1/n\). Write a recursive function for \(H_n\).
- Extend the recursive function for \(H_n\) (see above) with a parameter to keep track of the number of function calls. Write an iterative function for \(H_n\).
- The number of derangements of n elements is defined as \(d_0 = 1\), \(d_1 = 0\), and for \(n>1\): \(d_n = (n-1)(d_{n-1} + d_{n-2})\). Define a recursive Python function to compute \(d_n\). Use memoization to make the function efficient.
- Write an iterative version for the function
is_palindrome()of Lecture 8. - Define a class
Towerto represent a pile, with the operations to pop and push a disk. Use this class in a recursive hanoi function which prints all the moves.