Lecture 14: Substitution, Expansion, and Factorization¶
Substitution is one of the fundamental tools to work with expressions. Expansion is the counterpart of factorization.
Substitution¶
As a first application of substitution, we can replace an expression by a new variable to prevent expansion when we manipulate expression. Substitution is normally executed in sequence, but expressions are callable objects and calling an expression by keyword arguments performs the substitution simultaneously, as required when we want to permute the variables in an expression. Knowing the list of operands in an expression is useful. With string manipulations we can perform a pure syntactical substitution.
Suppose we would like to rewrite \((x+y)^2 + \frac{1}{(x+y)^2}\) into \(\frac{(x+y)^4 + 1}{(x+y)^2}\).
We consider then an expression in x and y
that we want to bring on the same denominator.
var('x,y')
p = (x+y)^2 + 1/(x+y)^2
print(p, 'has type', type(p))
If we want to bring the expression on a common denominator,
then we could try the factor() method.
p.factor()
The output is
(x^4 + 4*x^3*y + 6*x^2*y^2 + 4*x*y^3 + y^4 + 1)/(x + y)^2.
The factor expands the numerator, which is not what we want.
To shield (x+y)^2 from expanding,
we will save x+y into a new variable z.
Then we will factor the expression in z.
After this, we substitute z back to x + y.
var('z')
q = p.subs({(x+y): z})
print('after substitution of x+y into z :', q)
fq = q.factor()
print('after factoring :', fq)
qq = fq.subs(z=x+y)
print('after substitution of z into x+y :', qq)
And we see printed as output:
after substitution of x+y into z : z^2 + 1/z^2
after factoring : (z^4 + 1)/z^2
after substitution of z into x+y : ((x + y)^4 + 1)/(x + y)^2
To view the expression nicely typeset, we do
qq.show()
and then we see \(\frac{(x+y)^4 + 1}{(x+y)^2}\).
Observe that even when we submit a dictionary as argument
of the subs() method, the substitution happens in sequence
and not simultaneously. Suppose we want to permute the
variables in an expression. For example, we want to replace
a by b, b by c, and c by a.
Then the expression a + 2*b + 3*c turns into b + 2*c + 3*a
via a simultaneous substitution, that is: if the substitution
is executed simultaneously.
The simultaneous substitution of the variables in an expression is illustrated in Fig. 18.
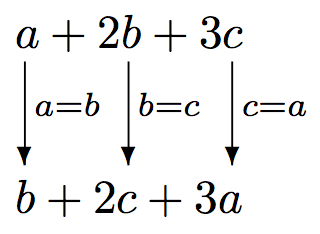
Fig. 18 Simultaneous substitution of the variables in an expression
as done by e(a=b, b=c, c=a) for e = a + 2*b + 3*c.¶
The sequential substitution of the variables in an expression is illustrated in Fig. 19.
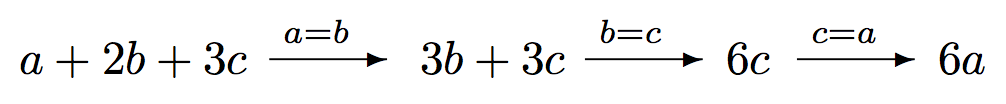
Fig. 19 Sequential substitution of the variables in an expression,
as done by e.subs(a=b).subs(b=c).subs(c=a) for e = a + 2*b + 3*c.¶
Expressions are callable objects and when we evaluate by keyword argument, then the substitution is executed simultaneously.
var('a,b,c')
e = a + 2*b + 3*c
print('the expression :', e)
print('substitution with dictionary argument :', e.subs({a:b, b:c, a:c}))
print('evaluation by keyword arguments :', e(a=b,b=c,c=a))
The result of e.subs({a:b, b:c, a:c}) turns out to be
the same as e(a=b, b=c, c=a) as those statements both
perform the substitution simultaneously.
Returning to the first application of substitution on p,
if we had tried to replace (x+y)^2 by z, then we
would have noticed that only the numerator changed.
Looking at the operands of p explains why this is.
print(p)
print(p.operands())
and we see that the list of operands is
[(x + y)^2, (x + y)^(-2)].
With string manipulation, we can perform a pure syntactical substitution.
s = str(p)
print(s)
t = s.replace('(x + y)^2', 'z')
print(t)
which then shows the string z + 1/z.
Knowing the list of operands, we can substitute (x+y)^2 by z^2
and (x+y)^(-2) by z^(-1).
p.subs({(x+y)^2:z, (x+y)^(-2):z^(-1)})
which will show the expression z + 1/z.
Expansion¶
When we give an expression in factored form, such as \((a + b + c) (x^3 + 9 x + 8)\) then we see that Sage does not expand the expression automatically. Why not? The main reason is expression swell.
var('a,b,c,x')
p = (a + b + c)*(x^3 + 9*x + 8)
print(p)
If we want to expand the expression,
then we apply the expand() method.
print(p.expand())
The expand() did too much, it expanded everything and
we have lost the structure of the polynomial in x.
Suppose we want to keep the factor (a + b + c) intact, what do we do then?
Well, we declare a new variable and substitute the expression
a + b + c to this new variable before calling the expand() method.
var('d')
dp = p.subs({a+b+c:d})
print(dp)
Now we expand and then replace d with the original a + b + c.
edp = dp.expand()
print(edp)
pp = edp.subs({d:(a+b+c)})
print(pp)
and we see
d*x^3 + 9*d*x + 8*d and
(a + b + c)*x^3 + 9*(a + b + c)*x + 8*a + 8*b + 8*c.
There is an alternative and shorter way to obtain the above result.
We view p as a polynomial in x with coefficients in QQ[a,b,c].
Converting p into the ring QQ[a,b,c][x] is straightforward:
q = QQ[a,b,c][x](p)
The outcome of print(q) is the same as the result
of the above print(pp).
The conversion of an expression into an element of a polynomial ring
of course only works if the expression is a polynomial.
Factorization¶
The opposite to expand is factor. We distinguish between exact, symbolic, and numeric factorization. A complete exact factorization is only possible if all the roots are rational numbers.
f = factor(x^2 - 1)
print(f, 'has type', type(f))
and we see the expression (x + 1)*(x - 1).
In a symbolic factorization, we add a formal root,
a so-called algebraic number.
For example, if we start with the rational numbers,
then we extend QQ with a root of an irreducible polynomial,
using the symbol a in the extended number field K.
y = polygen(QQ)
q = y^2 + 2
print(factor(q))
print(q.is_irreducible())
K.<a> = QQ.extension(q)
kq = (K[y])(q)
print(factor(kq))
Then the symbolic factorization is (x - a) * (x + a).
The numerical factorization happens always over a complex field.
z = polygen(CC)
print(factor(z^2 + 2))
and the numerical (approximate) factorization is
(x - 1.41421356237310*I) * (x + 1.41421356237310*I).
Assignments¶
Give the Sage commands to transform \((x+y)^2 + \frac{1}{x+y}\) into \(\frac{(x+y)^3 + 1}{x+y}\) and vice versa.
Give the Sage commands to transform \(x^2 + 2 x + 1 + \frac{1}{x^2 + 2 x + 1}\) into \(\frac{(x+1)^4 + 1}{(x+1)^2}\) and vice versa.
Give the Sage commands to transform \(x^3 - x y^2 - y x^2 + y^3 + x^2 - y^2\) into \((x^2 - y^2)(x-y+1)\).
Give the Sage commands to transform \((x + z^2 + 1)(y - z^2 - 1)\) into \(x y - x (z^2 + 1) + (z^2 + 1) y - (z^2 + 1)^2\).