Lecture 18: Defining Mathematical Functions

Expressions in SageMath are callable objects and for fast evaluation in machine numbers we have fast_callable objects. Although we may define functions with the Python def syntax, we can differentiate, integrate, and plot Sage functions. The simplest discontinuous functions are step functions.

Functions in SageMath and in Python

We can define functions as in Python, but also more directly.

f(x,y) = sin(x) + e^cos(y)
print(f, 'has type', type(f))

The print statement shows (x, y) |--> e^cos(y) + sin(x) and we see that a function is an expression.

print(f(2,pi))
print(f.integrate(x))

This shows e^(-1) + sin(2) and (x, y) |--> x*e^cos(y) - cos(x). Observe thus that, as we integrate a function, the result is again displayed as a function.

Let us explore the difference with Python functions.

def g(x,y):
    return sin(x) + e^cos(y)
print(g, 'has type', type(g))

Now the type of g is that of function. We cannot integrate a Python function, the command below does not work.

g.integrate(x)

because the function object has no attribute integrate. But because we are defining functions in SageMath, we can evaluate the function symbolically.

e = g(x,y)
print(e, 'has type', type(e))

and we see e^cos(y) + sin(x) has type <type 'sage.symbolic.expression.Expression'>

So we can turn an expression into a function.

h(x,y) = e
print(h, 'has type' ,type(h))
print(h.integrate(x))

We see that h is defined as a function that we can integrate.

Step Functions

Can we define step functions? Step functions are the simplest discontinuous functions.

print(unit_step, 'has type', type(unit_step))
print('at -3 :', unit_step(-3))
print('at 4 :', unit_step(4))

The unit_step is defined in the class sage.functions.generalized.FunctionUnitStep. For negative x values, the value of the unit step is zero, for positive x, the value is one. Let us look at the plot, for x between -1 and +1.

plot(unit_step, -1, 1, aspect_ratio=1)

Setting the aspect_ratio to 1 forces the plot to take the same scale on the horizontal as on the vertical axes. The unit step function is shown in Fig. 20.

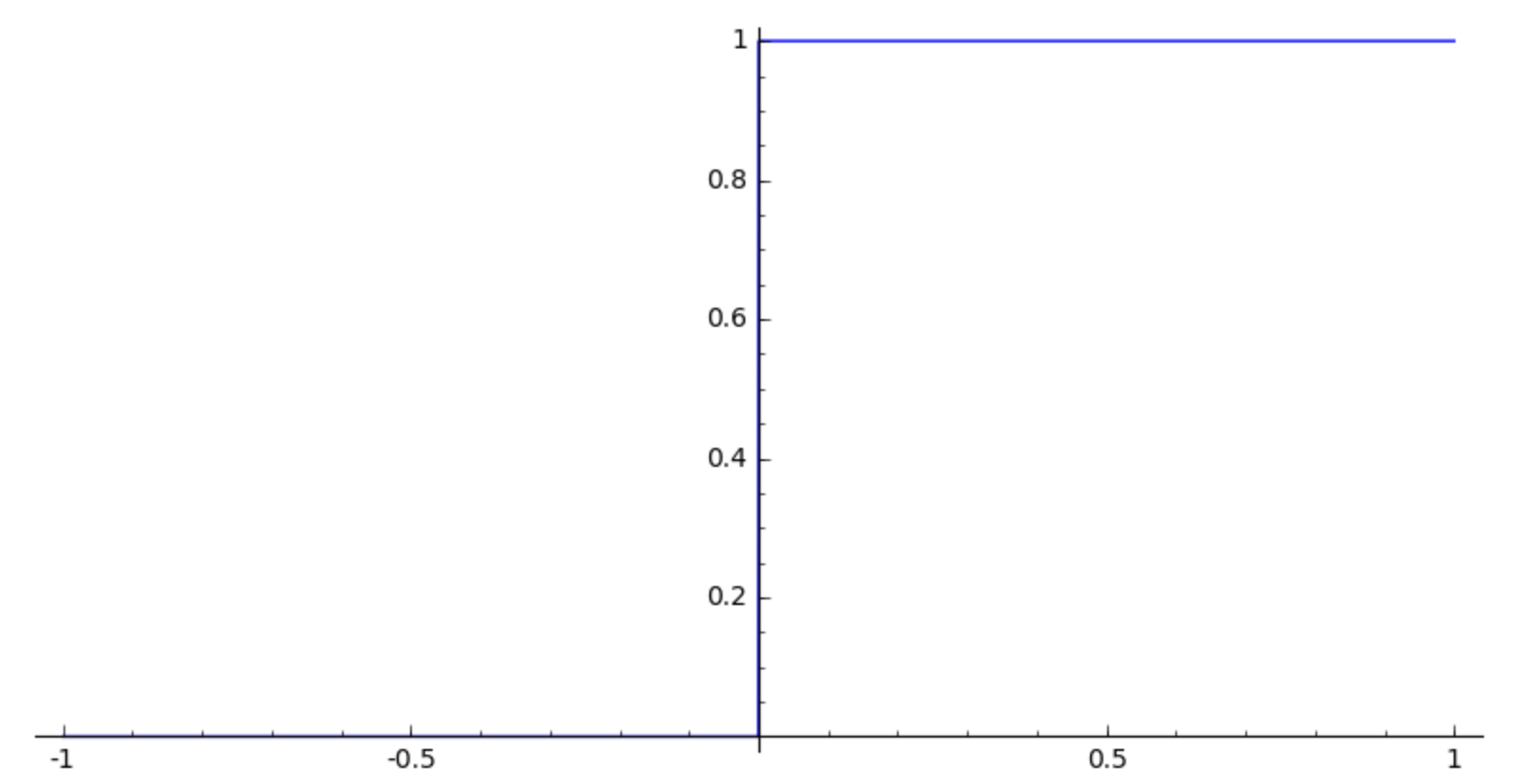
Fig. 20 The unit step function.

The derivative of the unit step function is the Dirac delta function.

diff(unit_step(x),x)

which shows dirac_delta(x).

We can take the definite integral of the unit step function.

integral(unit_step(x), (x, -3, 3))

and, as expected, the integral returns 3.

Another important discontinuous function is the Kronecker delta, which is a function in two variables returning 1 if both arguments are equal and returning 0 otherwise.

print(kronecker_delta(1,2))
print(kronecker_delta(1,1))

and we see 0 and 1 printed.

Piecewise Functions

We can make piecewise functions. For example,

\[\begin{split}f(x) = \left\{ \begin{array}{lcl} 1 & if & x < 1 \\ \infty & if & x = 1 \\ x^2 & if & x > 1 \\ \end{array} \right.\end{split}\]

To define this piecewise function, we use piecewise.

f = piecewise([((-infinity, 1), 1), ([1,1], infinity), ((1, infinity), x^2)] )
print(f)

Combining Functions

We can combine functions. Suppose we want to make a 3-step staircase function, defined as follows: f(x) = 0 for x < 0, f(x) = 1/3 for x in [0,1), f(x) = 2/3 for x in [1,2) and f(x) = 1 for x >= 2.

f(x) = unit_step(x)/3 + unit_step(x-1)/3 + unit_step(x-2)/3
plot(f(x),(x,-1,3),aspect_ratio=0.5)

The figure is shown in Fig. 21.

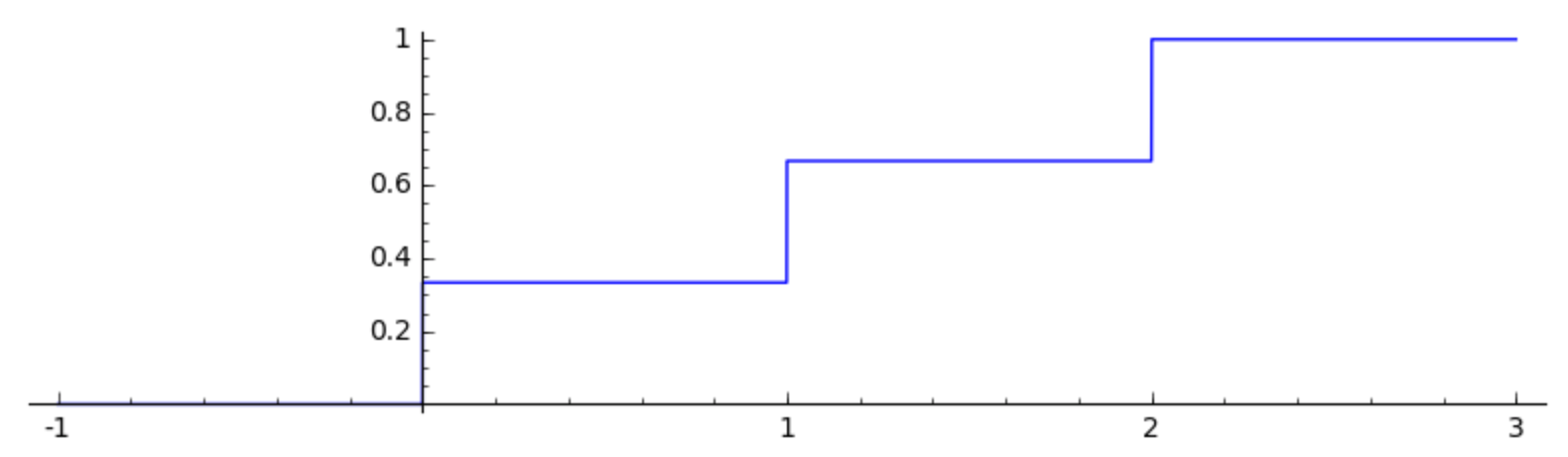
Fig. 21 A staircase function.

Assignments

1. Define the following function:

   \[\begin{split}f(x) = \left\{ \begin{array}{lcl} 3x+1 & if & x ~odd \\ x/2 & if & x ~even \end{array} \right.\end{split}\]

   Apply f recursively starting at a random integer number \(n\), computing \(f(n)\), then \(f(f(n))\), \(f(f(f(n)))\), and so on. Do you observe a pattern?

2. Run the code below in a SageMath session. Explain what happens. Hint: consider the evaluation of a Python function at a variable in turning an expression into a SageMath function.

   def h(x):
       if x<2:
           return 0
       else:
           return x-2
   plot(h(x), (x, -2, 2))
   

3. Define a piecewise linear function that is zero for negative values of x and takes the value x/2 for positive values of x.

4. Make a hat function f(x) with definition f(x) = 0 for x less than -1 or larger than 1; and f(x) = 1 for x in the interval [-1,+1]. Show with a plot that your definition is correct.

5. Consider the formula

   \[{\displaystyle \pi = \sum_{k=0}^\infty \frac{1}{16^k} \left( \frac{4}{8 k + 1} - \frac{2}{8 k + 4} - \frac{1}{8 k + 5} - \frac{1}{8 k + 6} \right)}.\]

   Make a function f(k) that returns the value of what is in the \(( \cdot )\) in the sum for \(\pi\).

   Use this function in a list comprehension to compute the first 100 hexadecimal digits of \(\pi\).

   How accurate is this approximation for \(\pi\)? Write the magnitude of the error.