Lecture 19: Recursive Functions¶

Recursion is a very powerful tool to define function in a compact way. Unfortunately, a direct implementation of a recursive function may lead to very inefficient code. Using dictionaries in Python we can apply memoization and obtain efficient recursive functions without having to rewrite the recursion into an iteration.

Memoization in Python¶

The Fibonacci numbers are defined recursively. The first two numbers are zero and one. The next numbers are the sum of the two previous ones. To compute the \(n\)-th Fibonacci number, we follow the three rules listed below.

\(F(0) = 0\)
\(F(1) = 1\)
\(F(n) = F(n-1) + F(n-2)\), if \(n > 1\).

The Python function below follows those three rules in a nested branching statement.

def fibonacci(n):
    """
    Returns the n-th Fibonacci number.
    """
    if n == 0:
        result = 0
    elif n == 1:
        result = 1
    else:
        result = fibonacci(n-1) + fibonacci(n-2)
    return result

Let us look at the first 10 Fibonacci numbers:

[fibonacci(n) for n in range(11)]

and this shows the list of the first 10 Fibonacci numbers: [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55].

The problem is that it gets very efficient as n grows.

timeit('fibonacci(20)')

We see 25 loops, best of 3: 15.8 ms per loop as executed on a 3.1 GHz Intel Core i7 Mac OS X 10.12.6. Let us continue:

timeit('fibonacci(21)')

shows 25 loops, best of 3: 24.7 ms per loop and we do it once more, for the 22-nd Fibonacci number:

timeit('fibonacci(22)')

and we see 5 loops, best of 3: 40.3 ms per loop. Observe that 15.8 + 24.7 = 40.5. The time to compute the 22-nd Fibonacci number equals the sum of the time to compute the 20-th and the 21-st Fibonacci number. The timings thus also follow a similar pattern as the Fibonacci number are increase exponentially.

If we examine the tree of function calls, then we see why this definition leads to a very inefficient function. We abbreviate fibonacci() by f().

f(5)
 +-- f(4)
 |    +-- f(3)
 |    |    +-- f(2)
 |    |    |    +-- f(1) = 1
 |    |    |    +-- f(0) = 0
 |    |    +-- f(1) = 1
 |    +-- f(2)
 |         +-- f(1) = 1
 |         +-- f(0) = 0
 +-- f(3)
      +-- f(2)
      |    +-- f(1) = 1
      |    +-- f(0) = 0
      +-- f(1) = 1

Even for a very simple case as the 5-th Fibonacci number, we see that the f(3) gets computed thrice and f(2) twice.

If we draw the tree with LabelledBinaryTree, starting at the leaves F(0) and F(1), then we arrive at the iterative version of the algorithm.

L0 = LabelledBinaryTree([], label='F(0)')
L1 = LabelledBinaryTree([], label='F(1)')
L2 = LabelledBinaryTree([L0, L1], label='F(2)')
ascii_art(L2)

The two base cases are displayed in Fig. 22 as they occur in the computation of F(2).

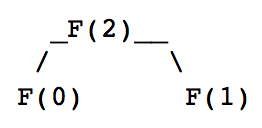
_images/figfibfun2callstree.png — Fig. 22 The computation of `F(2)` as `F(0) + F(1)`.¶

Consider the computation of F(3), F(4), and F(5), following the iterative algorithm to compute F(5).

L3 = LabelledBinaryTree([L1, L2], label='F(3)')
L4 = LabelledBinaryTree([L2, L3], label='F(4)')
L5 = LabelledBinaryTree([L3, L4], label='F(5)')
ascii_art(L5)

The result of ascii_art(L5) is shown in Fig. 23.

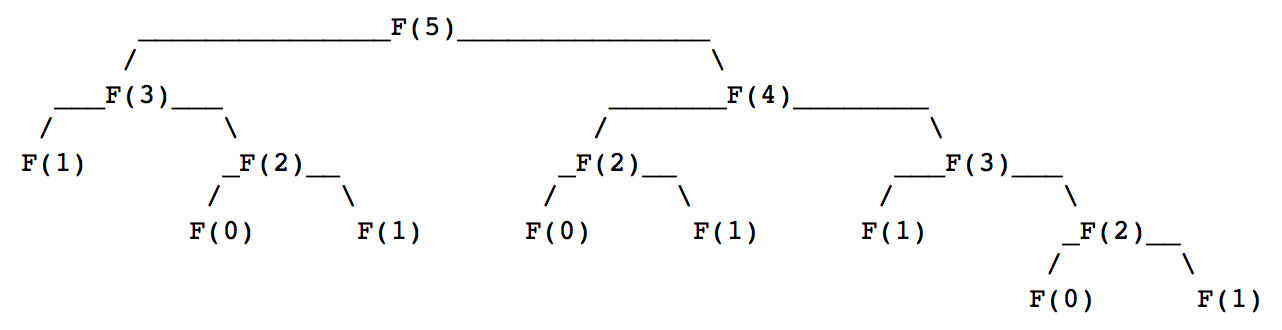
_images/figfibfuncallstree.png — Fig. 23 The tree of function calls in the computation of `F(5)`.¶

With default arguments we can have functions store data. In the memoized version of the recursive Fibonacci function we use a dictionary to store the values for previous calls. The keys in the dictionary are the arguments of the function and the values are what the function returns. With each call to the function, the dictionary is consulted and only if there is no key for the argument, then the body of the function is executed.

def memoized_fibonacci(n, D={}):
    """
    Returns the n-th Fibonacci number, using D to
    memoize the values computed in previous calls.
    """
    if n in D:
        return D[n]   # dictionary lookup
    else:
        if n == 0:
            result = 0
        elif n == 1:
            result = 1
        else:
            result = memoized_fibonacci(n-1) + memoized_fibonacci(n-2)
    D[n] = result     # store the new result
    return result

Now if we time this new function.

timeit('memoized_fibonacci(20)')

we see 625 loops, best of 3: 590 ns per loop.

[memoized_fibonacci(n) for n in range(30)]

In the memoized version, we have replaced a number of function calls that grows exponentially in \(n\) by an amount of storage that grows linearly in \(n\). For memoization to work, it is important that the anount of storage remains proportional to the dimension of the problem.

Memoization in SageMath¶

In symbolic computing we define functions to compute expressions. Chebyshev polynomials are orthogonal polynomials, available in SageMath via the function chebyshev_T.

t3 = chebyshev_T(3, x)
print(t3, 'has type', type(t3))

and we see 4*x^3 - 3*x has type <type 'sage.symbolic.expression.Expression'>.

The 3-terms recurrence to define a Chebyshev polynomial of degree \(n\) in the variable \(x\) is

\(T(0,x) = 1\),
\(T(1,x) = x\), and
\(T(n,x) = 2 x T(n-1,x) - T(n-2,x)\).

The straightforward definition based on this 3-terms recurrence is below in the function T. Observe the application of expand(). We normalize the Chebyshev polynomials into the fully expanded form.

def T(n, x):
    """
    Returns the n-th Chebyshev polynomial in x.
    """
    if n == 0:
        return 1
    elif n == 1:
        return x
    else:
        return expand(2*x*T(n-1, x) - T(n-2, x))

To test the function, we compute the third Chebyshev polynomial.

T(3, x)

and indeed, we see 4*x^3 - 3*x. We can check the efficiency of the implementations.

print('the Chebyshev in Maxima :')
timeit('chebyshev_T(10,x)')
print('our direct function T :')
timeit('T(10,x)')

The output is

the Chebyshev in Maxima : 625 loops, best of 3: 799 µs per loop
our direct function T : 25 loops, best of 3: 10.2 ms per loop

We apply the memoization technique from Python to the SageMath function T and call the memoized function mT. Our T had two parameters:

n is the degree of the polynomial, and
x is the variable in the polynomial.

Therefore, the keys in the dictionary will be a tuple (n, x).

def mT(n, x, D = {}):
    """
    Returns the n-th Chebyshev polynomial in x,
    using memoization with the dictionary D.
    """
    if (n, x) in D:
        return D[(n, x)]  # dictionary lookup
    else:
        if n == 0:
            result = 1
        elif n == 1:
            result = x
        else:
            result = expand(2*x*mT(n-1, x) - mT(n-2, x))
    D[(n, x)] = result    # store the new polynomial
    return result

To check its correctness, we do again print(mT(3,x)) to see 4*x^3 - 3*x. Let us check how much faster the memoized version is.

timeit('mT(10,x)')

and we obtain 625 loops, best of 3: 491 ns per loop.

Assignments¶

The Bell numbers \(B(n)\) are defined by \(B(0) = 1\) and

\[\begin{split}B(n) = \sum_{i=0}^{n-1} \left( \begin{array}{c} n-1 \\ i \end{array} \right) B(i),\end{split}\]

for \(n > 0\). They count the number of partitions of a set of \(n\) elements.

Write a recursive function to compute the Bell numbers. The binomial coefficient \(\left( \begin{array}{c} n-1 \\ i \end{array} \right)\) is computed by binomial(n-1,i). Make sure your procedure is efficient enough to compute B(50).
The Stirling numbers of the first kind \(c(n,k)\) satisfy the recurrence

\[c(n,k) = - (n-1) c(n-1,k) + c(n-1,k-1), \mbox{ for } n \geq 1 \mbox{ and } k \geq 1,\]

with the initial conditions that \(c(n,k) = 0\) if \(n \leq 0\) or \(k \leq 0\), except \(c(0,0) = 1\).
1. Write an efficient recursive function, call it stirling1 to compute \(c(n,k)\).
  
  The \(n\) must be the first argument of stirling1 while \(k\) is its second argument, e.g.: for \(n = 100\) and \(k = 33\), stirling1(100,33) should return \(c(100,33)\).
2. How many digits does the number \(c(100,33)\) have? Give also the SageMath command(s) to obtain this number.
The \(n\)-th Chebychev polynomial is also often defined as \(\cos(n \arccos(x))\).

Give the definition of the function C which takes on input the degree \(n\) and a value for \(x\).

Thus C(n,x) returns \(\cos(n \arccos(x))\) while C(10,0.512) returns the value of the 10-th Chebychev polynomial at 0.512. Compare this value with chebyshev_T(10,0.512).
Let L(n,x) denote a special kind of the Laguerre polynomial of degree n in the variable x.

We define L(n,x) by three rules:
1. L(0,x) = 1,
2. L(1,x) = x, and
3. for any degree n > 1: n*L(n,x) = (2*n-1-x)*L(n-1,x) - (n-1)*L(n-2,x).
Write a SageMath function Laguerre that returns L(n,x). Make sure your function can compute the 50-th Laguerre polynomial.
Denote the composite Trapezoidal rule for \(\int_a^b f(x) dx\) using \(2^n\) intervals by T(n,f,a,b).

We can define T(n, f, a, b) recursively by two rules:
1. T(0, f, a, b) = (f(a) + f(b))*(b-a)/2 and
2. T(n, f, a, b) = T(n-1, f, a, (a+b)/2) + T(n-1, f, (a+b)/2, b), for n > 0.
Do the following.
1. Write a recursive SageMath function for T.
2. Explain how you can define T so that f is never evaluated twice at the same point.
  
  Illustrate using n = 5 in T for the numerical approximation of \(\int_0^1 \cos(x) dx\).
The Bernoulli polynomials are defined by

\[B_0(x) = 1, \quad B_k(x) = k \left( \int_0^x B_{k-1}(t) dt - \int_0^1 \left( \int_0^x B_{k-1}(t) dt \right) dx \right), k > 0.\]
1. Write an efficient recursive function B which returns \(B_k(x)\) in expanded form. The arguments of B are the degree \(k\) and the name of the variable \(x\) in the polynomial \(B_k(x)\). Thus, to compute \(B_{50}(x)\), we type B(50,x).
2. What is the coefficient of \(x^{49}\) in the polynomial \(B_{50}(x)\)? Give also the SageMath command to obtain this coefficient.

Lecture 19: Recursive Functions¶

Memoization in Python¶

Memoization in SageMath¶

Assignments¶

Table of Contents

Previous topic

Next topic

This Page