Lecture 1: Introduction¶

In this first lecture we define the problem statement, give an application, recall Newton’s method and formulate a statement of the theorem of Bézout.

Problem Statement¶

We consider as given a system \(f({\bf x}) = {\bf 0}\) of \(N\) polynomials \(f = (f_1,f_2,\ldots,f_N)\) in \(n\) unknowns \({\bf x} = (x_1,x_2,\ldots,x_n)\). Depending on whether \(N > n\), \(N = n\), or \(N < n\), we call the system respectively overdetermined, square, and underdetermined. The coefficients of the polynomials are complex numbers and may be known with limited accuracy, as the result of empirical data.

We distinguish three different forms of the input polynomials:

The degree is the main characteristic of the polynomials.

The degree is usually the first attribute of a polynomial, we speak of quadratic, cubic, quartic, and quintic polynomials when the degree is respectively 2, 3, 4, and 5.

A polynomial of degree \(d\) is dense if all monomials of degree \(d\) or less occur with nonzero coefficient. In general, dense polynomials of degree \(d\) in \(n\) variables have a number of monomials which grows exponentially. Consider Pascal’s formula:

\[\begin{split}\left( \begin{array}{c} d + n \\ d \end{array} \right) = \left( \begin{array}{c} d + (n-1) \\ d \end{array} \right) + \left( \begin{array}{c} (d-1) + n \\ d-1 \end{array} \right).\end{split}\]

The first term of the sum counts the number of monomials of degree \(d\) while the second term counts the number of monomials of degree strictly less than \(d\).

As the size of dense polynomials grows exponentially, dense polynomials are not practical to work with.
A finite set \(A\) of exponent vectors is the support of a polynomial.

Then we denote a polynomial \(p({\bf x})\) in multi-index notation as

\[p({\bf x}) = \sum_{{\bf a} \in A} c_{\bf a} {\bf x}^{\bf a}, \quad c_{\bf a} \in {\mathbb C} \setminus \{ 0 \}, \quad {\bf a} = (a_1,a_2,\ldots,a_n).\]

For example, \(p(x_1,x_2) = c_{12} x_1 x_2^2 + c_{20} x_1^2 + c_{11} x_1 x_2 + c_{00}\) uses a multi-index notation for the nonzero coefficients. While degree(\(p\)) = 3, a quick drawing of all possible third degree monomials in two variables, shows that a dense cubic has 10 coefficients. But our example is sparse: \(\#A = 4\).

Most polynomials occurring in practical applications are \(sparse\), i.e.: only relatively few monomials occur with nonzero coefficient. The sparse structure of a polynomial is then represented by its support or often also by the convex hull of the support, the so-called Newton polygon (or polytope in arbitrary dimensions).
A program is given which evaluates the polynomial.

Considering polynomials as functions is done typically in numerical analysis. While evaluating polynomials seems at first sight rather straightforward, finding the optimal way to evaluate a polynomial in several variables is not so obvious. Except for dense polynomials – where the nested Horner scheme is best – the optimal evaluation strategy is often dependent on the type of application.

Since the coefficients of the polynomials are considered to be of limited accuracy, the algorithms we will study will find approximate solutions. In case there are finitely many solutions, we are interested in having a sharp bound on the number of solutions. When there are infinitely many solutions, like surfaces and curves, we are interested in knowing the degrees of the components and the number of irreducible factors.

Inverse Kinematics¶

The design of mechanisms is one application area for polynomial systems. As a first application, consider a planar robot arm, consisting of two links and two joints. The position of the hand of the robot is determined by the angles the two links make. See the figure Fig. 1

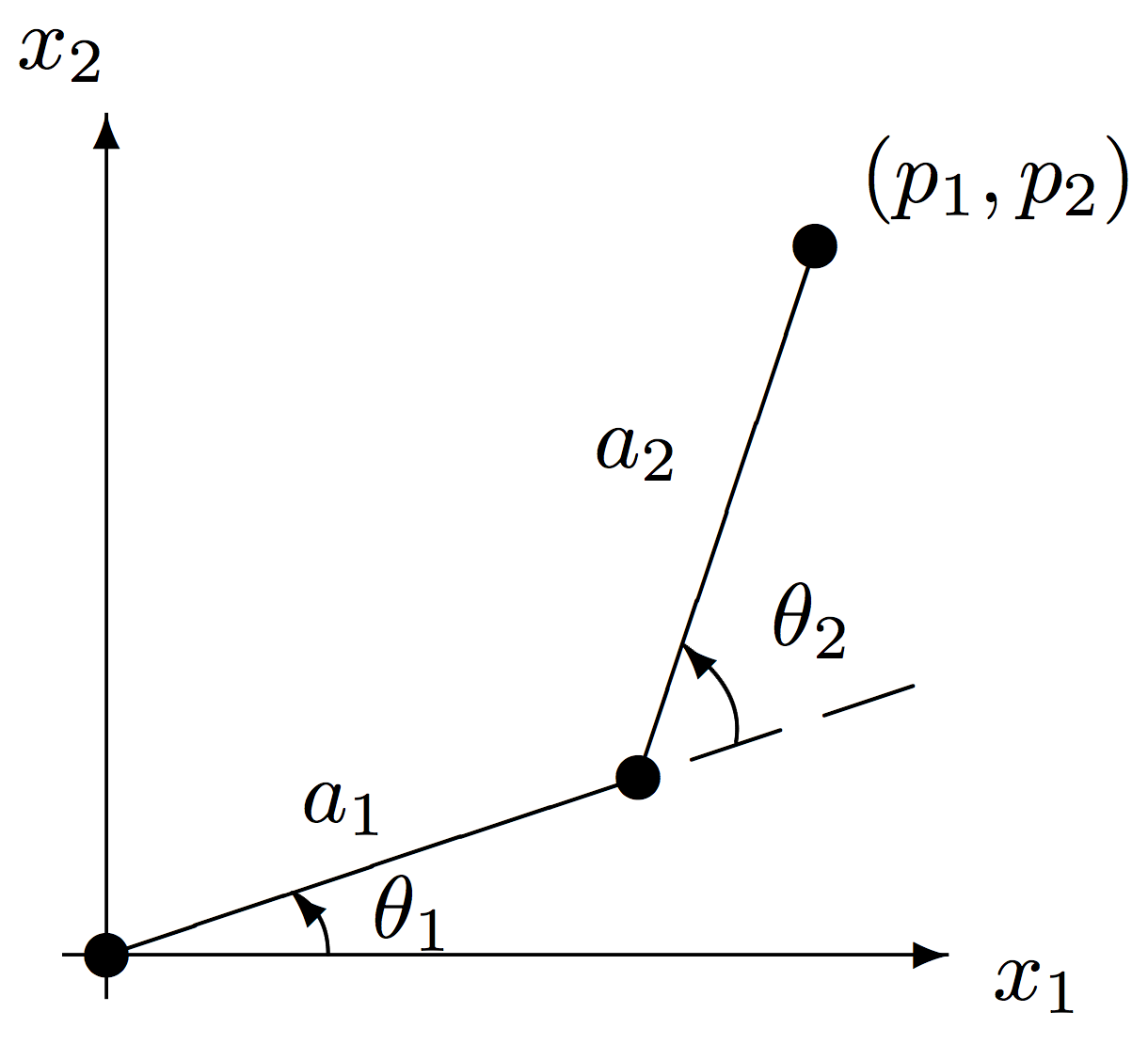
Fig. 1 The inverse kinematics of a two dimensional robot arm.

Given the coordinates \((p_1,p_2)\) for the desired position of the robot hand, the inverse kinematics problem is to determine the values for the angles \((\theta_1,\theta_2)\) so that the hand reaches the desired position.

To formulate the equations, consider the transformation of the coordinate system so that the new origin is at the first joint, rotated so that the first coordinate axis is aligned with the first link.

\[\begin{split}\left[ \begin{array}{c} x_1 \\ x_2 \\ 1 \end{array} \right] = \underbrace{ \left[ \begin{array}{ccc} c_1 & -s_1 & 0 \\ s_1 & c_1 & 0 \\ 0 & 0 & 1 \end{array} \right]}_{rotate~by~\theta_1} \underbrace{ \left[ \begin{array}{ccc} 1 & 0 & a_1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right]}_{translate} \left[ \begin{array}{c} x'_1 \\ x'_2 \\ 1 \end{array} \right], \quad s_1 = \sin(\theta_1), c_1 = \cos(\theta_1).\end{split}\]

If we denote product of the rotation-translation matrices by

\[\begin{split}A_1 = \left[ \begin{array}{ccc} c_1 & -s_1 & c_1 a_1 \\ s_1 & c_1 & s_1 a_1 \\ 0 & 0 & 1 \end{array} \right],\end{split}\]

and similarly \(A_2\) for the coordinate transformation using the second link and the second angle, then we write the two coordinate transformations by the matrix equation

\[\begin{split}\left[ \begin{array}{c} x_1 \\ x_2 \\ 1 \end{array} \right] = A_1 A_2 \left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] = \left[ \begin{array}{c} c_1 c_2 a_2 - s_1 s_2 a_2 + c_1 a_1 \\ s_1 c_2 a_2 + c_1 s_2 a_2 + s_1 a_1 \\ 1 \end{array} \right],\end{split}\]

which expresses that the hand of the robot has coordinates \((0,0)\) in the third coordinate system and \((x_1,x_2)\) in the first coordinate system. So the system we must solve is

\[\begin{split}\left\{ \begin{array}{c} c_1 c_2 a_2 - s_1 s_2 a_2 + c_1 a_1 = p_1 \\ s_1 c_2 a_2 + c_1 s_2 a_2 + s_1 a_1 = p_2 \\ c_1^2 + s_1^2 = 1 \\ c_2^2 + s_2^2 = 1 \\ \end{array} \right.\end{split}\]

with the last two equations respectively expressing \(\sin^2(\theta_1) + \cos^2(\theta_1) = 1\) and \(\sin^2(\theta_2) + \cos^2(\theta_2) = 1\). With given numbers for the lengths of links \(a_1\) and \(a_2\) and values for the coordinates \((p_1,p_2)\), we have a system of four quadratic equations to solve the inverse position problem. This example was taken from Chapter 10 of the book of Alexander Morgan on Solving polynomial systems using continuation for engineering and scientific problems reissued as a SIAM Classic in Applied Mathematics in 2009. Polynomial systems play a prominent role in the design of linkages.

Newton’s Method¶

Locally, if we have a good guess about a solution, we may obtain a more accurate solution using Newton’s method. The idea for Newton’s method has its origin in Taylor series.

For \(n=1\), the Taylor expansion of a function \(f\) about \(x\) is

\[f(x + \Delta x) = f(x) + \Delta x \frac{f'(x)}{1!} + (\Delta x)^2 \frac{f''(x)}{2!} + (\Delta x)^3 \frac{f'''(x)}{3!} + \cdots = \sum_{j=0}^\infty (\Delta x)^j \partial_j f(x).\]

To derive Newton’s method, we truncate the expansion at the second term:

\[f(x + \Delta x) = f(x) + \Delta x f'(x) + O((\Delta x)^2).\]

If we have that at \(x\): \(f(x) \approx 0\), and we look for \(\Delta x\) so that \(f(x + \Delta x) = 0\), then we solve the truncated expansion for \(\Delta x\) and obtain \(\Delta x = - f(x)/f'(x)\) as the update to the current approximation \(x\). This formula gives rise to a sequence \(x_k\) of successive approximations of a root, given by

\[x_{k+1} := x_k - \frac{f(x_k)}{f'(x_k)}, \quad {\rm for}~ k = 0,1,\ldots\]

which is well defined provided the derivative \(f'\) does not vanish. If \(f'\) does not vanish at the root, then the sequence converges quadratically for \(x_0\) close enough to the root, i.e.: if \(f(x^*) = 0\): \(|| x_{k+1} - x^* || \leq || x_k - x^* ||^2\). We can formalize the algorithm using MATLAB (or Octave):

function [x,fail] = newton(f,df,x,eps,N)
%
%  Applies Newton's method to the function f, with derivative in df,
%  starting at the point x.  It produces a sequence of approximations.
%  Stops when the sequence reaches the point x where
%  |f(x)| < eps or when two consecutive points in the sequence
%  have distance less than eps apart from each other.
%  Failure is reported (fail = 1) when the accuracy requirement
%  is not satisfied in N steps; otherwise fail = 0 on return.
%
%  Example :
%  >> [x,fail] = newton('sin','cos',pi/4,1e-8,10)
%
fprintf('running the method of Newton...\n');
fx = feval(f,x);
for i = 1:N
   dx = fx/feval(df,x);
   x = x - dx;
   fx = feval(f,x);
   fprintf('  x = %e, dx = %e, f(x) = %e\n', x, dx, fx);
   if (abs(fx) < eps) | (abs(dx) < eps)
      fail = 0;
      fprintf('succeeded after %d steps\n', i);
      return;
   end
end
fprintf('failed requirements after %d steps\n', N);
fail = 1;

For \(n=2\), we generalize the Taylor expansion of \(f\) as

\[\begin{split}\begin{array}{l} f(x_1 + \Delta x_1, x_2 + \Delta x_2) = f(x_1,x_2) + \frac{\Delta x_1}{1!} \frac{\partial f}{\partial x_1}(x_1,x_2) + \frac{\Delta x_2}{1!} \frac{\partial f}{\partial x_2}(x_1,x_2) \\ ~~~+ \frac{(\Delta x_1)^2}{2!} \frac{\partial^2 f}{\partial x_1^2}(x_1,x_2) + \frac{(\Delta x_1)(\Delta x_2)}{1! 1!} \frac{\partial^2 f}{\partial x_1 \partial x_2}(x_1,x_2) + \frac{(\Delta x_2)^2}{2!} \frac{\partial^2 f}{\partial x_2^2}(x_1,x_2) + \cdots = {\displaystyle \sum_{|{\bf a}| = 0}^\infty (\Delta {\bf x})^{\bf a} \partial_{\bf a} f({\bf x})}, \end{array}\end{split}\]

where for \({\bf a} = (a_1,a_2,\ldots,a_n)\) the operator \(\partial_{\bf a}\) is defined by

\[\partial_{\bf a} = \frac{1}{a_1! a_2! \cdots a_n!} \frac{\partial^{|{\bf a}|}} {\partial^{a_1}_1 \partial^{a_2}_2 \cdots \partial^{a_n}_n}, \quad {\rm with}~ |{\bf a}| = a_1 + a_2 + \cdots + a_n.\]

If a function is differentiable, then it means that locally we may replace the function by a linear function. For \(\Delta {\bf x} \approx 0\), \(f({\bf x}) \approx\) linear. To derive Newton’s method in several variables, we write the Taylor expansions in matrix form:

\[\begin{split}f({\bf x} + \Delta {\bf x}) = f({\bf x}) + \left[ \begin{array}{cccc} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_N}{\partial x_1} & \frac{\partial f_N}{\partial x_2} & \cdots & \frac{\partial f_N}{\partial x_n} \\ \end{array} \right](\Delta {\bf x}) + O((\Delta {\bf x})^2).\end{split}\]

The matrix which appears in this expansion is the Jacobian matrix, which we denote by \(J_f\). Let \(N = n\), so \(f\) is a square system.

Assume that \({\bf x}\) is a current approximation for the root \({\bf x}^*\) (for which \(f({\bf x}^*) = 0\)) and that we wish to find \(\Delta {\bf x}\) so that \({\bf x} + \Delta {\bf x} = {\bf x}^*\). Ignoring the second order terms in the Taylor expansion of \(f({\bf x} + \Delta {\bf x}) = 0\), we have \(f({\bf x}) + J_f \Delta {\bf x} = {\bf 0}\). If \(J_f\) is invertible, we may solve for \(\Delta {\bf x}\) as solution of the linear system \(J_f \Delta {\bf x} = -f({\bf x})\) which gives the update which brings us closer to the root \({\bf x}^*\).

We say that \({\bf x}^*\) is a regular root if \(\det(J_f({\bf x}^*)) \not= 0\). Otherwise, \({\bf x}^*\) is a singular root. Singular roots occur at multiple solutions and solutions that are nonisolated.

A solution \({\bf x}^*\) is isolated if there exists a ball centered at \({\bf x}^*\) with a nonzero radius that contains no other solution of the system. When a solution is not isolated it lies on a curve or surface. Note that real solutions may occur as isolated real points on a complex curve, i.e.: there is no other real solution in its neighborhood. Consider for example the single equation \(x^2 + y^2 = 0\) defining a pair of complex conjugated lines \(y = \pm \sqrt{-1} x\) through the point \((0,0)\). The point \((0,0)\) is just as nonisolated as all the other solutions satisfying \(x^2 + y^2 = 0\), but it is the only real solution and thus one could regard it as an isolated real solution.

Newton’s method is one of the most important algorithms to solve nonlinear problems. An advanced treatment is described in the book of Peter Deuflhard on Newton Methods for Nonlinear Problems. Affine Invariance and Adaptive Algorithms, published by Springer-Verlag in 2004.

The Theorem of Bézout¶

For general nonlinear systems, we cannot make a statement about the number of isolated solutions. For polynomial systems, the main theorem of algebraic geometry is the theorem of Bézout. We can view this theorem as a generalization of the fundamental theorem of algebra:

the fundamental theorem of algebra

A polynomial of degree d in one variable with nonzero leading coefficient has exactly d complex roots, where each root is counted with its multiplicity.

For a univariate polynomial p, the multiplicity of z as a root of p is k if in addition to \(p(z) = 0\) also all derivatives of p up to order \(k-1\) vanish at z.

If we consider a system of two univariate polynomials, of degrees \(d_1\) and \(d_2\) respectively, then it is obvious that there are \(d_1 \times d_2\) isolated solutions. The theorem of B’ezout says that a system can have no more isolated solutions than the product of the degrees of the polynomials. Formally we can write

theorem of Bézout on the number of isolated solutions

Consider a system \(f({\bf x}) = {\bf 0}\) of n equations \(f = (f_1,f_2,\ldots,f_n)\) in n unknowns \({\bf x} = (x_1,x_2,\ldots,x_n)\).

The number of isolated solutions in \({\mathbb C}^n\) is bounded by

\[D = \prod_{i=1}^n \deg(f_i).\]

We call D the total degree of the system. Also here the solutions have to be counted with multiplicities, although a precise definition of the multiplicity is much harder for polynomial systems. The total degree is a somewhat crude but important complexity bound for polynomial systems.

One proof of the theorem of Bézout works by deforming the polynomials in the system into polynomials in one variable. This kind of proof by deformation leads to homotopy continuation methods for solving polynomial systems.

Software for Algebraic Geometry¶

A crude classification for software suitable for algebraic geometry distinguishes between the big M’s (commercial software) and free open source packages.

The big M’s are Maple, Mathematica, Magma, and MATLAB (purchased MuPAD for symbolic computations).
Free and open source (GNU GPL): CoCoA, Macaulay2, Singular. ApCoCoA stands for Applied Computations in Computer Algebra. SageMath contains Singular as a component. We can use Octave as a free alternative to MATLAB.
Some specialized software packages, e.g.: PHCpack has a developing Python interface phcpy.

The focus of this course is actually not on the implementation but more on the study of symbolic-numerical algorithms to solve systems of polynomial equations.

Finally, we end with a list of conferences related to computational algebraic geometry:

ACA: Applications of Computer Algebra
CASC: Computer Algebra in Scientific Computation
MEGA: Effective Methods in Algebraic Geometry
ISSAC: International Symposium on Symbolic and Algebraic Computation
SIAM conference on Algebraic Geometry
SNC: Symbolic-Numeric Computation

Bibliography¶

E. Bézout. General Theory of Algebraic Equations. Princeton University Press, 2006. Translated by Eric Feron. Original French edition published as Théorie générale des équations algébriques by Ph.-D. Pierres, Paris, 1779.
L. Blum, F. Cucker, M. Shub, and S. Smale. Complexity and Real Computation. Springer-Verlag, 1998.
P. Deuflhard. Newton Methods for Nonlinear Problems. Affine Invariance and Adaptive Algorithms. Springer-Verlag, 2004.
T.Y. Li. Solving polynomial systems. The Mathematical Intelligencer, 9(3):33-39, 1987.
J.M. McCarthy. Geometric Design of Linkages. Springer-Verlag, 2000.
A. Morgan. Solving polynomial systems using continuation for engineering and scientific problems. Prentice-Hall, 1987. Published as volume 57 in the series Classics in Applied Mathematics, SIAM, 2009.
T. Sauer. Numerical Analysis. Pearson Addison-Wesley, 2006.

Exercises¶

The notion of a sparse polynomial changes when one considers the number of vertices which span its Newton polygon, i.e.: a dense polynomial may have a Newton polygon which is spanned by only a few vertices. Give an example of two polynomials which have the same Newton polygon where one polynomial is sparse and the other is dense.
How many arithmetical operations are needed to evaluate a polynomial of degree d in n variables with a Horner scheme? Start with \(n=1\) and generalize.
How many solutions do you expect to the inverse position problem for the planar robot arm with two links? Make a case analysis.
Use Maple (or any other computer algebra system) to solve the inverse position problem for the planar robot arm with two links? In your answer, give the Maple instructions you used and report on the results Maple returns to you. Open source alternatives to Maple, e.g.: CoCoA, Macaulay2, Sage, or Singular may be used as well.
Generalize the MATLAB script newton so that it also works for systems. You can of course also use Octave. Give a numerical example to illustrate that your generalized newton script works.
Apply the theorem of Bézout to bound the number of isolated solutions to the system which must be solved for the inverse position problem for the planar robot arm with two links. Can you derive an equivalent formulation for this problem which leads to a system with lower total degree? (Hint: consider multiplying the matrix equation by \(A_1^{-1}\).)
Use Maple (or SageMath, or any other computer algebra system) and make a worksheet or notebook to derive the polynomial equations for the inverse kinematics problem. Also derive the alternative formulation suggested in the previous exercise, multiplying with \(A^{-1}\).