Lecture 2: Elimination Methods¶
In this lecture we define projective coordinates, give another application, explain the Sylvester resultant method, illustrate how to cascade resultants to compute discriminant, and then state the main theorem of elimination theory. Because of the algebraic nature of the methods, we assume the coefficients to be exact (in \(\mathbb Z\) or \(\mathbb Q\)) and all calculations (with Maple or Sage) are performed with exact arithmetic and/or with the manipulation of symbolic coefficients.
Projective Coordinates¶
Consider the problem of intersecting two circles in the plane. Without loss of generality, we may choose our coordinate system so that the x-axis passes through the centers of the circles and let the first circle be centered at the origin and have radius one. Let then the second circle have radius \(r\) and denote the coordinates of its center by \((c,0)\). The corresponding system is then
By elimination (subtracting from the second equation the first) we see that there can be at most two isolated roots.
Just like two parallel lines meet at infinity, the system has solutions at infinity. We can compute these solutions by transforming the system into projective coordinates. The map \(\psi\)
defines an embedding of \({\mathbb C}^n\) into projective space \({\mathbb P}^n\), mapping points into equivalence classes. While most common, note that $psi$ is just a projective transformation, we will encounter other ones. The equivalence relation \(\sim\) is defined by
From the embedding defined by the map \(\psi\) we see that as \(x_0 \rightarrow 0\), that then the coordinates \(x_i \rightarrow \infty\), for \(i = 1,2,\ldots,n\). So a point with \(x_0 = 0\) lies at infinity.
To find the solution at infinity of the system of the two intersecting circles, we embed it into projective space replacing first \(x_1\) by \(x_1/x_0\), \(x_2\) by \(x_2/x_0\) and then multiplying by \(x_0^2\), to obtain
Notice how every monomial in the system has now the same degree. We say that the system is now homogeneous. To find the solutions at infinity, we set \(x_0 = 0\) and solve \(x_1^2 + x_2^2 = 0\). Since coordinates in \({\mathbb P}^2\) are determined only up to a factor, we may set \(x_1 = 1\) and find then \(x_2 = \pm \sqrt{-1}\).
Thus we find \([0 : 1 : \pm \sqrt{-1} ]\) as the two solutions at infinity of the problem of intersecting two circles. Except for the case when there are infinitely many solutions, the theorem of B|eacute|zout in projective space states that there are always as many solutions as the product of the degrees.
The importance of projective space to practical applications lies in the scaling of the coordinates. Computing solutions with huge coordinates leads to an ill-conditioned numerical problem. Embedding the problem into projective space provides a numerically more favorable representation of the solutions with huge coordinates. Obviously, the coefficients of the polynomials also naturally belong to a projective space, because the solution set does not change as we multiply the polynomials with a nonzero coefficient.
Molecular Configurations¶
The picture at the left in figure Fig. 2 represents a robot arm with 6 revolute joints. The middle picture is a configuration of six atoms. Placing these two pictures on top of each other suggests that the bonds between the atoms correspond to the joints of the robot arm while the links of the robot arm correspond to the atoms. Note that the configurations are spatial.
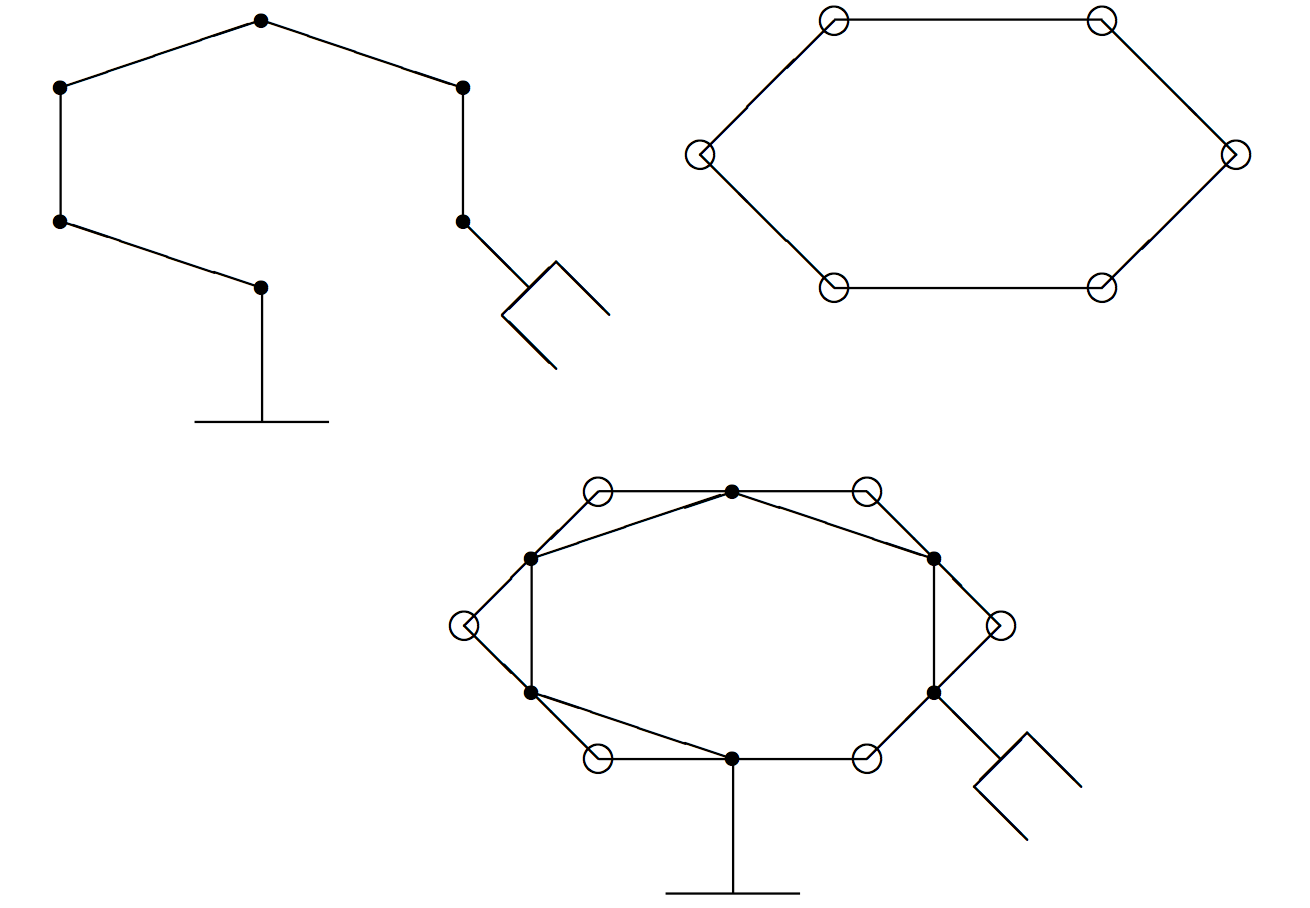
Fig. 2 A robot arm with 6 joints and a molecular configuration.
To determine the configuration, we label the atoms clockwise as \(p_1, p_2, \ldots, p_6\). Consider then the three triangles \(T_1, T_2\), and \(T_3\), spanned respectively by the respective triplets \((p_1,p_2,p_6)\), \((p_2,p_3,p_4)\), and \((p_4,p_5,p_6)\). Denote by \(\theta_i\), for \(i=1,2,3\), the angle between \(T_i\) and the base triangle spanned by \((p_2,p_4,p_6)\). Fixing the distances between the atoms and angles \(\theta_i\) determines the configuration.
To design a configuration, we must solve the system
where the \(\alpha_{ij}\) are input coefficients.
Instead of solving directly for the cosines and sines of the angles, we can obtain a smaller system transforming to half angles: letting \(t_i = \tan(\theta_i/2)\), for \(i=1,2,3\), implies \(\cos(\theta_i) = (1-t_i^2)/(1+t_i^2)\) and \(\sin(\theta_i) = 2t_i/(1+t_i^2)\). After clearing denominators, we obtain the system
where the \(\beta_{ij}\) are the input coefficients.
Note that the second system has fewer equations. However the equations of the second system are of degree four. While the decrease in dimension is often seen as favorable for symbolic elimination methods, numerically, dealing with polynomials of higher degree may often be challenging.
This application is described in greater detail in the 1995 PhD thesis of Ioannis Emiris along with elimination methods to solve such systems.
Resultants¶
The following lemma is taken from the book by Cox, Little and O’Shea:
Lemma
Two polynomials f and g have a common factor \(\Leftrightarrow\) there exist two nonzero polynomials A and B
such that \(A f + B g = 0\), with \(\deg(A) < \deg(g)\) and \(\deg(B) < \deg(f)\).
Proof.
\(\Rightarrow\) Let \(f = f_1 h\) and \(g = g_1 h\), then \(A = -g_1\) and \(B = -f_1\): \(A f + B g = - g_1 f_1 h + f_1 g_1 h = 0\).
\(\Leftarrow\) Suppose f and g have no common factor. By the Euclidean algorithm we then have that \(\mbox{GCD}(f,g) = 1 = \widetilde{A} f + \widetilde{B} g\). Assume \(B \not= 0\). Then \(B = 1 B = (\widetilde{A} f + \widetilde{B} g ) B\). Using \(B g = - Af\) we obtain \(B = (\widetilde{A} B - \widetilde{B} A) f\). As \(B \not= 0\), it means that \(\deg(B) \geq \deg(f)\) which gives a contradiction. Thus f and g must have a common factor. \(\square\)
The importance of this lemma is that via linear algebra we will get a criterion on the coefficients of the polynomials f and g to decide whether they have a common factor. Consider for example \(f(x) = a_0 + a_1 x + a_2 x^2 + a_3 x^3\) and \(g(x) = b_0 + b_1 x + b_2 x^2\). If f and g have a common factor, then there must exist two nonzero polynomials \(A(x) = c_0 + c_1 x\) and \(B(x) = d_0 + d_1 x + d_2 x^2\) such that \(A(x) f(x) + B(x) g(x) = 0\). Executing the polynomial multiplication and requiring that all coefficients with x are zero leads to a homogeneous system in the coefficients of A and B:
In matrix form, we have
The matrix of the linear system is called the Sylvester matrix of f and g. Only if its determinant is zero can the linear system have a nontrivial solution. Observe that the determinant leads to a polynomial in the coefficients of the polynomials. This polynomial is called the resultant.
With the computer algebra system Maple,
we can eliminate x from two polynomials f and g,
via the following commands:
[> sm := LinearAlgebra[SylvesterMatrix](f,g,x);
[> rs := LinearAlgebra[Determinant](sm);
If we are given a polynomial system, we can eliminate one variable by viewing the equations as polynomials in that one variable while hiding the other variables as part of the symbolic coefficients. This is the basic principle of elimination methods.
Geometrically, the process of elimination corresponds to projecting the solution set onto a space with fewer variables. While dealing with fewer variables sounds attractive, it is not too hard to find examples where the elimination introduces additional singular solutions.
While the setup in this lecture is symbolic, for problems with approximate coefficients, the determinant computation is replaced by determining the numerical rank via a singular value decomposition or via a QR decomposition.
Cascading Resultants to Compute Discriminants¶
Resultants can be used to define discriminants. For a polynomial with indeterminate coefficients we may ask for a condition on the coefficients for which there are multiple roots, i.e.: where both the polynomial and its derivative vanish. The discriminant of f can thus be seen as the resultant of f and its derivative.
The notion of a discriminant is not limited to polynomials in one variable. We can say that the system
has exactly two solutions
except for those c and r satisfying
The polynomial \(D(c,r)\) is the discriminant for the system. The discriminant variety is the solution set of the discriminant. For the example, it is shown in figure Fig. 3.
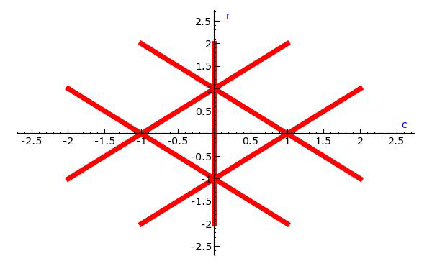
Fig. 3 A discriminant variety.
By symmetry, we can classify the regular solutions into four different categories.
Given a system f with parameters, a straightforward method to compute the discriminant takes 2 steps:
- Let \(E\) be \((f,\det(J_f))\), where \(J_f\) is the Jacobian matrix of f.
- Eliminate from E all the indeterminates, using resultants.
What remains after elimination is an expression in the parameters: the discriminant.
For the example, we consider:
With SageMath, we proceed as follows (note that sage: is the prompt
in a terminal session):
sage: x,y,c,r = var('x,y,c,r')
sage: f1 = x^2 + y^2 - 1
sage: f2 = (x-c)^2 + y^2 - r^2
sage: J = matrix([[diff(f1,x),diff(f1,y)],[diff(f2,x),diff(f2,y)]])
sage: dJ = det(J)
sage: print f1, f2, dJ
2 2
y + x - 1
2 2 2
y + (x - c) - r
4 x y - 4 (x - c) y
To use the resultants of Singular, we declare a ring of rational numbers
and convert the three polynomials: f1, f2, and dJ to this ring.
sage: R.<x,y,c,r> = QQ[]
sage: E = [R(f1),R(f2),R(dJ)]
sage: print E
[x^2 + y^2 - 1, x^2 + y^2 - 2*x*c + c^2 - r^2, 4*y*c]
Cascading resultants, we first eliminate x and then eliminate y. To eliminate x we combine the equations pairwise:
sage: e01 = singular.resultant(E[0],E[1],x)
sage: e12 = singular.resultant(E[1],E[2],x)
sage: print e01, e12
4*y^2*c^2+c^4-2*c^2*r^2+r^4-2*c^2-2*r^2+1 16*y^2*c^2
After elimination of y we obtain the discriminant:
sage: discriminant = singular.resultant(e01,e12,y)
sage: factor(R(discriminant))
(256) * (c - r - 1)^2 * (c - r + 1)^2 * (c + r - 1)^2 * (c + r + 1)^2 * c^4
Notice the ring conversion before the factorization.
With Macaulay2, we obtain the same result. Consider the commands in the script:
R = ZZ[c,r][x,y]
f = {x^2 + y^2 - 1, (x-c)^2 + y^2 - r^2}
F = ideal(f)
jac = jacobian(F)
J = determinant(jac)
r01 = resultant(f#0, f#1, x)
r12 = resultant(f#1, J, x)
disc = resultant(r01, r12, y)
print factor(disc)
The print shows
4 2 2 2 2
(c) (c - r - 1) (c - r + 1) (c + r - 1) (c + r + 1) (256)
The Main Theorem of Elimination Theory¶
Resultants provide a constructive proof for the following theorem.
Theorem
Let \(V \subset {\mathbb P}^n\) be the solution set of a polynomial system. Then the projection of \(V\) onto \({\mathbb P}^{n-1}\) is again the solution set of a system of polynomial equations.
The use of projective coordinates is needed. Consider for instance \(x_1 x_2 - 1 = 0\). The projection of this hyperbola onto the coordinate axes leads to a line minus a point. A line minus a point is not the solution set of a polynomial. This observation points at another drawback of resultants (in addition to the potential introduction of singular solutions): the solutions of the resultant may include solutions at infinity which are spurious to the original problem.
In Theorem 14.1 of the book of D. Eisenbud we find the main theorem of elimination theory formulated in more general terms, but also with an outline of a constructive proof using resultants, see exercise 14.1 on page 318.
Bibliography¶
- D. Cox, J. Little, and D. O’Shea. Ideals, Varieties and Algorithms. An Introduction to Computational Algebraic Geometry and Commutative Algebra. Undergraduate Texts in Mathematics. Springer–Verlag, second edition, 1997.
- D. Eisenbud. Commutative Algebra with a View Toward Algebraic Geometry, volume 150 of Graduate Texts in Mathematics. Springer-Verlag, 1995.
- I.Z. Emiris and B. Mourrain. Computer algebra methods for studying and computing molecular conformations. Algorithmica, 25(2-3):372-402, 1999. Special issue on algorithmic research in Computational Biology, edited by D. Gusfield and M.-Y. Kao.
Exercises¶
For the system of the two intersection circles determine the exceptional values for the parameters c and r for which there are infinitely many solutions. Justify your answer.
Derive the formulas for the transformation which uses half angles, we used to transform the system with the \(\alpha\) coefficients into the system with the \(\beta\) coefficients.
Consider \(f(x) = a x^2 + b x + c\). Use resultant methods to compute the discriminant of this polynomial.
Use resultants to solve the system
\[\begin{split}\left\{ \begin{array}{rcl} x_1 x_2 - 1 & = & 0 \\ x_1^2 + x_2^2 - 1 & = & 0. \\ \end{array} \right.\end{split}\]Consider the system
\[\begin{split}\left\{ \begin{array}{rcl} x^2 + y^2 - 2 & = & 0 \\ x^2 + \frac{y^2}{5} - 1 & = & 0. \end{array} \right.\end{split}\]Show geometrically by making a plot of the two curves that elimination will lead to polynomials with double roots. Compute resultants (as univariate polynomials in x or y) and show algebraically that they have double roots.
Consider as choice in system for the \(\beta_{ij}\) coefficients the matrix (second instance in the Emiris-Mourrain paper of 1999):
\[\begin{split}\left[ \begin{array}{ccccc} -13 & -1 & -1 & 24 & -1 \\ -13 & -1 & -1 & 24 & -1 \\ -13 & -1 & -1 & 24 & -1 \\ \end{array} \right].\end{split}\]Try to solve the system using these coefficients. How many solutions do you find?
Extend the discriminant computation for the ellipse \((\frac{x}{a})^2 + (\frac{y}{b})^2 = 1\) and the circle \((x-c)^2 + y^2 = r^2\). Interpret the result by appropriate projections of the four dimensional parameter space onto a plane.
Examine the intersection of three spheres. What are the components of its discriminant variety?