Four Sample Questions

The four questions in this lecture are representative for some of the topics covered in the course.

Scaled Speedup

Benchmarking of a program running on a 12-processor machine shows that 5% of the operations are done sequentially, i.e.: that 5% of the time only one single processor is working while the rest is idle.

Compute the scaled speedup.

The formula for scaled speedup is \(\displaystyle S_s(p) \leq \frac{st + p(1-s)t}{t} = s + p(1-s) = p + (1-p) s\). Evaluating this formula for \(s = 0.05, p = 12\) yields

\[S_s(12) = 12 + (1-12) 0.05 = 11.45.\]

Network Topologies

Show that a hypercube network topology has enough connections for a fan-in gathering of results.

Consider Fig. 76, which illustrates the fan-in algorithm for 8 nodes.

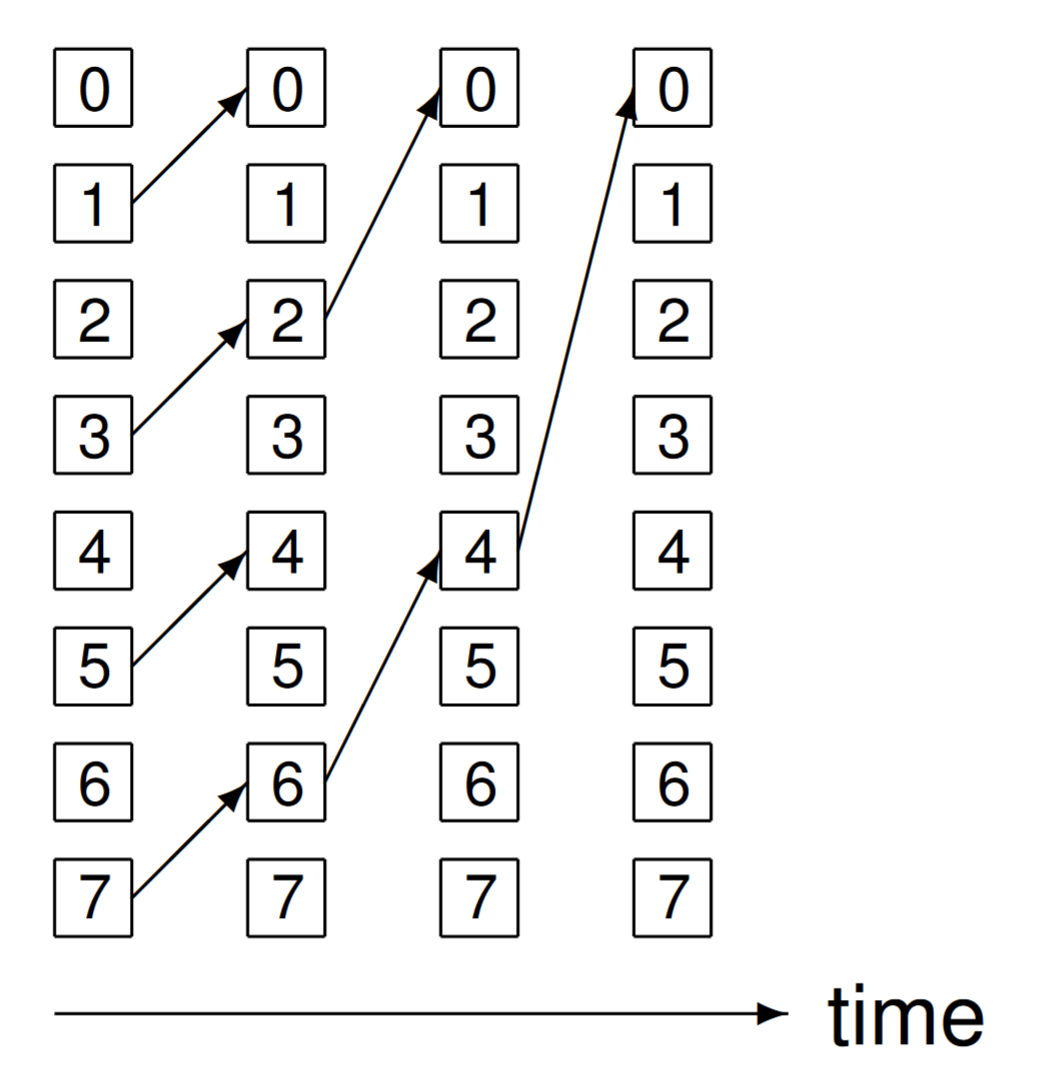
_images/figfaninreview.png

Fig. 76 Fanning in the result for 8 nodes.

For the example in Fig. 76, three steps are executed:

  1. 001 \(\rightarrow\) 000; 011 \(\rightarrow\) 010; 101 \(\rightarrow\) 100; 111 \(\rightarrow\) 110

  2. 010 \(\rightarrow\) 000; 110 \(\rightarrow\) 100

  3. 100 \(\rightarrow\) 000

To show a hypercube network has sufficiently many connections for the fan-in algorithm, we proceed via a proof by induction.

  • The base case: we verified for 1, 2, 4, and 8 nodes.

  • Assume we have enough connections for a \(2^k\) hypercube.

    We need to show that we have enough connections for a \(2^{k+1}\) hypercube:

    1. In the first \(k\) steps:

      • node 0 gathers from nodes \(1, 2, \ldots 2^k-1\);

      • node \(2^k\) gathers from nodes \(2^k+1, 2^k+2, \ldots,2^{k+1} - 1\).

    2. In step \(k+1\): node \(2^k\) can send to node 0, because only one bit in \(2^k\) is different from 0.

Task Graph Scheduling

Given are two vectors \({\bf x}\) and \({\bf y}\), both of length \(n\), with \(x_i \not= x_j\) for all \(i \not= j\). Consider the code below:

for i from 2 to n do
    for j from i to n do
        y[j] = (y[i-1] - y[j])/(x[i-1] - x[j])

  1. Define the task graph for a parallel computation of \({\bf y}\).

  2. Do a critical path analysis on the graph to determine the upper limit of the speedup.

For \(n=4\), the numbers are in the table below:

\[\begin{split}\begin{array}{ccc} {\displaystyle y_2 = \frac{y_1 - y_2}{x_1 - x_2}} & & \\ \vspace{-2mm} \\ {\displaystyle y_3 = \frac{y_1 - y_3}{x_1 - x_3}} & {\displaystyle y_3 = \frac{y_2 - y_3}{x_2 - x_3}} & \\ \vspace{-2mm} \\ {\displaystyle y_4 = \frac{y_1 - y_4}{x_1 - x_4}} & {\displaystyle y_4 = \frac{y_2 - y_4}{x_2 - x_4}} & {\displaystyle y_4 = \frac{y_3 - y_4}{x_3 - x_4}} \\ \end{array}\end{split}\]

If the computations happen row by row, then there is no parallelism. Observe that the elements in each column can be computed independently from each other. Label the computation on row \(i\) and column \(j\) by \(T_{i,j}\) and consider the graph in Fig. 77.

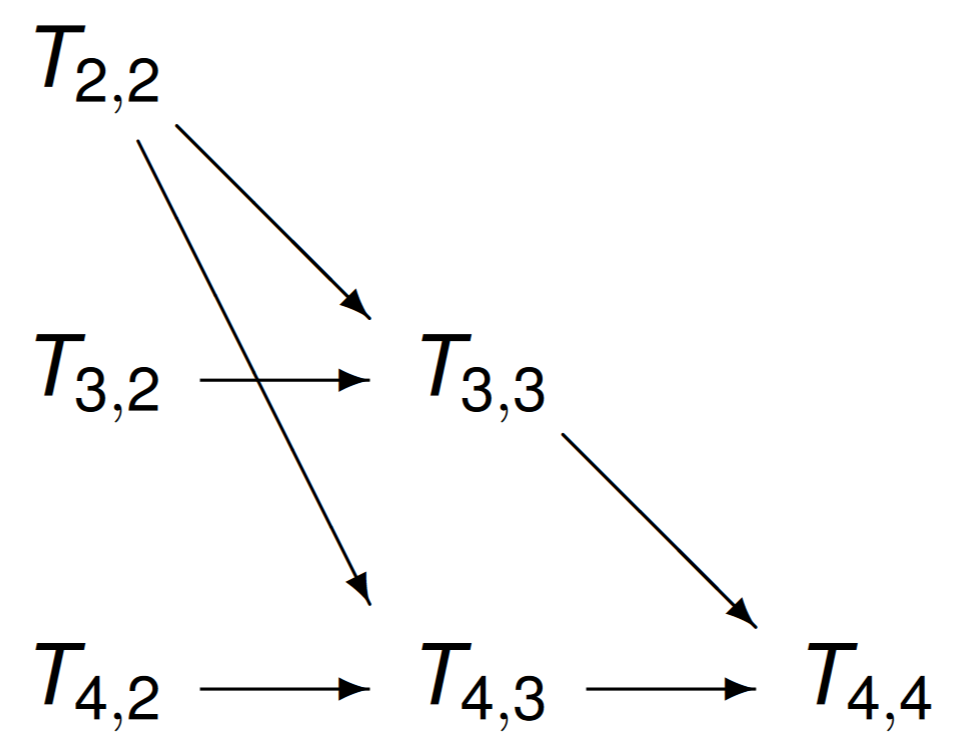
_images/figtaskgraphreview.png

Fig. 77 The task graph for \(n=4\).

For \(n = 4\), with 3 processors, it takes three steps to compute the table. The speedup is 6/3 = 2. Each path leading to \(T_{4,4}\) has two edges or three nodes. So, the length of the critical path is 2.

For any \(n\), with \(n-1\) processors, it takes \(n-1\) steps, leading to a speedup of \(n(n-1)/2 \times 1/(n-1) = n/2\).

Compute Bound or Memory Bound

A kernel performs 36 floating-point operations and seven 32-bit global memory accesses per thread.

Consider two GPUs \(A\) and \(B\), with the following properties:

  • \(A\) has peak FLOPS of 200 GFLOPS and 100 GB/second as peak memory bandwidth;

  • \(B\) has peak FLOPS of 300 GFLOPS and 250 GB/second as peak memory bandwidth.

For each GPU, is the kernel compute bound or memory bound?

The CGMA ratio of the kernel is \(\displaystyle \frac{36}{7 \times 4} = \frac{36}{28} = \frac{9}{7} \frac{\mbox{operations}}{\mbox{byte}}\).

Taking the ratio of the peak performance and peak memory bandwidth of GPU \(A\) gives \(200/100 = 2\) operations per byte. As \(9/7 < 2\), the kernel is memory bound on GPU \(A\).

Alternatively, it takes GPU \(A\) per thread \(\displaystyle \frac{36}{200 \times 2^{30}}\) seconds for the operations and \(\displaystyle \frac{28}{100 \times 2^{30}}\) seconds for the memory transfers. As \(0.18 < 0.28\), more time is spent on transfers than on operations.

For GPU \(B\), the ratio is \(300/250 = 6/5\) operations per byte. As \(9/7 > 6/5\), the kernel is compute bound on GPU \(B\).

Alternatively, it takes GPU \(B\) per thread \(\displaystyle \frac{36}{300 \times 2^{30}}\) seconds for the operations and \(\displaystyle \frac{28}{250 \times 2^{30}}\) seconds for the memory transfers. As \(0.12 > 0.112\), more time is spent on computations than on transfers.