Fall 2024 Midterm Questions

The four questions below appeared on the midterm exam of Fall 2024.

Question 1 : Isoefficiency

Consider the communication and computation costs (as functions of dimension \(n\) and number of processors \(p\)) in the running times \(t^{(A)}(n,p)\) and \(t^{(B)}(n,p)\) of two programs, respectively \(A\) and \(B\):

\[\begin{array}{lll} {\displaystyle t^{(A)}(n,p) = t^{(A)}_{\rm comm}(n,p) + t^{(A)}_{\rm comp}(n,p),} & {\displaystyle t^{(A)}_{\rm comm}(n,p) = n \log(p),} & {\displaystyle t^{(A)}_{\rm comp}(n,p) = n^2/p,} \end{array}\]

\[\begin{array}{lll} {\displaystyle t^{(B)}(n,p) = t^{(B)}_{\rm comm}(n,p) + t^{(B)}_{\rm comp}(n,p),} & {\displaystyle t^{(B)}_{\rm comm}(n,p) = p + n^2 p,} & {\displaystyle t^{(B)}_{\rm comp}(n,p) = n^3/p.} \end{array}\]

Which program scales best? Use isoefficiency to justify your answer.

Illustrate with values for \(p\) between from 2 and 256, and for \(n\) between 10,000 and 100,000.

Evaluating the efficiencies for both programs gives Table 19 and Table 20, indexed by the number of processors in 2, 4, 8, 16, 32, 64, 128, 256, in the rows, and for the columns by the dimensions in 10000, 20000, 50000, 100000.

Table 19 efficiency of program \(A\)

	10000	20000	50000	100000
2	99.98	99.99	100.00	100.00
4	99.92	99.96	99.98	99.99
8	99.76	99.88	99.95	99.98
16	99.36	99.68	99.87	99.94
32	98.43	99.21	99.68	99.84
64	96.30	98.12	99.24	99.62
128	91.78	95.71	98.24	99.11
256	83.00	90.71	96.07	97.99

Table 20 efficiency of program \(B\)

	10000	20000	50000	100000
2	99.97	99.99	99.99	100.00
4	99.85	99.93	99.97	99.99
8	99.37	99.69	99.87	99.94
16	97.51	98.74	99.49	99.75
32	90.72	95.13	98.00	98.99
64	70.95	83.01	92.43	96.07
128	37.91	54.97	75.32	85.92
256	13.24	23.38	43.28	60.41

As the efficiency of program \(A\) is better than program \(B\) for increasing number of processors and dimensions, program \(A\) scales best.

Question 2 : the roofline model

A processor has 800 GFLOPS as peak performance and 400 GB/s as peak memory bandwidth.

The arithmetic intensity of a computation is 3 flops per byte.

1. Given the processor specifications, draw the roofline model.

   Apply your model to justify whether the computation is compute bound or memory bound.

2. If the arithmetic intensity of the computation is 1 flop per byte, then what is the maximal performance the computation can attain?

The roofline model is drawn in Fig. 78.

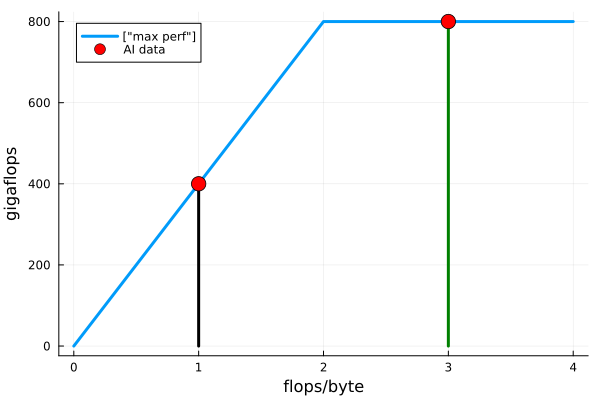
Fig. 78 Roofline model for 800 GFLOP/s and 400 GB/s.

On Fig. 78 we see two vertical lines. The first vertical line at 1 flop per byte contains the points of the possible performance, capped at 400 Gigaflops. At 1 flop per byte, the computation is memory bound. At 3 flops per byte, the maximum performance is 800 Gigaflops and the computation is compute bound.

Question 3 : tasking for enumeration

Consider three sets \(A = \{ a_1, a_2, \ldots, a_n \}\), \(B = \{ b_1, b_2, \ldots, b_n \}\), \(C = \{ c_1, c_2, \ldots, c_n \}\) of vertices in a tripartite graph \(G\) with edges in the set \(E\).

Each edge \(e \in E\) is a pair of the form \((a_i, b_j)\) or \((b_i, c_j)\), for \(i\) and \(j\) in \(\{1,2,\ldots,n \}\).

A matching is a subset of \(E\) where every element of \(A\), \(B\), and \(C\) occurs exactly once.

Consider the straightforward enumeration of all triplets to compute all matchings in \(G\).

1. Explain how tasking can be applied to speed up the enumeration.

2. What speedup do you expect? Relate the speedup to \(n\) and the size of \(E\).

Below is the outline of a possible solution.

1. The matching consists of a set of triplets \((a, b, c)\), where each \(a\), \(b\), \(c\) occurs exactly once in each triplet, \((a, b)\) and \((b, c)\) are edges.

   In exploring the search space, we can enumerate the triplets as follows, for each edge \((u, v) \in E\), consider the matching once with, and once without \((u, v)\), spawning two tasks for each case, with \((u, v) \in A \times B\) or \((u, v) \in B \times C\).

   Each task maintains its path of selected edges and set of triplets.

2. The number of possible edges grows as \(n\) choose 2 squared, as an upper bound between the edges between vertices of sets \(A\) and \(B\), and combined with all edges of vertices of sets \(B\) and \(C\). The search space grows much faster than we can scale the number of threads and the search space can be explored independently by many threads.

   With \(p\) threads, we expect the search space to be explored \(p\) times faster, and we may hope for an optimal speedup.

   Superlinear speedup could occur if one task finds a matching when less than 1/\(p\)-th of the search space has been explored, where \(p\) is the number of threads, but then if we want only one matching, and the question asked for all matchings.

Question 4 : CGMA ratio

Consider the kernel below.

__global__ SumOfSquares ( int n, float *x, float *y )
{
    int bdx = blockIdx.x;
    int tdx = threadIdx.x;
    int offset = bdx*n;

    y[tdx] = 0.0;
    for(int i=0; i<n; i++)
       y[tdx] = y[tdx] + x[offset+i]*x[offset+i];
}

1. Compute the CGMA ratio for this kernel.

2. Explain how the use of registers and shared memory improves the CGMA ratio.

Below is an outline of a possible solution.

1. The CGMA ratio is \(\displaystyle \frac{2n}{4n+1}\).

2. Using two registers xi and yr, as below

   __global__ SumOfSquares ( int n, float *x, float *y )
   {
       int bdx = blockIdx.x;
       int tdx = threadIdx.x;
       int offset = bdx*n;
       float xi;
       float yr = 0.0;
   
       for(int i=0; i<n; i++)
       {
          xi = x[offset+i];
          yr = yr + xi*xi;
       }
       y[tdx] = yr;
   }
   

   improves the CGMA ratio to \(\displaystyle \frac{2n}{n+1}\).