Four Sample Questions

The four questions in this lecture are representative for some of the topics covered in the course.

Limits on Speedup

In a computation, one fifth of all operations must be performed sequentially.

What is the maximum speedup that can be obtained with ten processors?

Justify your answer.

We apply Amdahl’s Law. Consider a job that takes time \(t\) on one processor. Let \(R\) be the fraction of \(t\) that must be done sequentially, \(R = 0.2\).

The formula for speedup on \(p\) processors is \(\displaystyle S_s(p) \leq \frac{t}{Rt + \frac{(1-R)t}{p}} = \frac{1}{R + \frac{1-R}{p}} \leq \frac{1}{R} = 5\).

For ten processors:

\[S(10) \leq \frac{1}{\frac{1}{5} + \frac{8}{100}} = \frac{100}{28}.\]

Space Time Diagram

Consider a 4-stage pipeline, where each stage requires the same amount of processing time.

Draw the space time diagram to process 10 units.

Use the diagram to justify the speedup.

The space time diagram for 4 processors \(P_0\), \(P_1\), \(P_2\), and \(P_3\) is shown in Fig. 155.

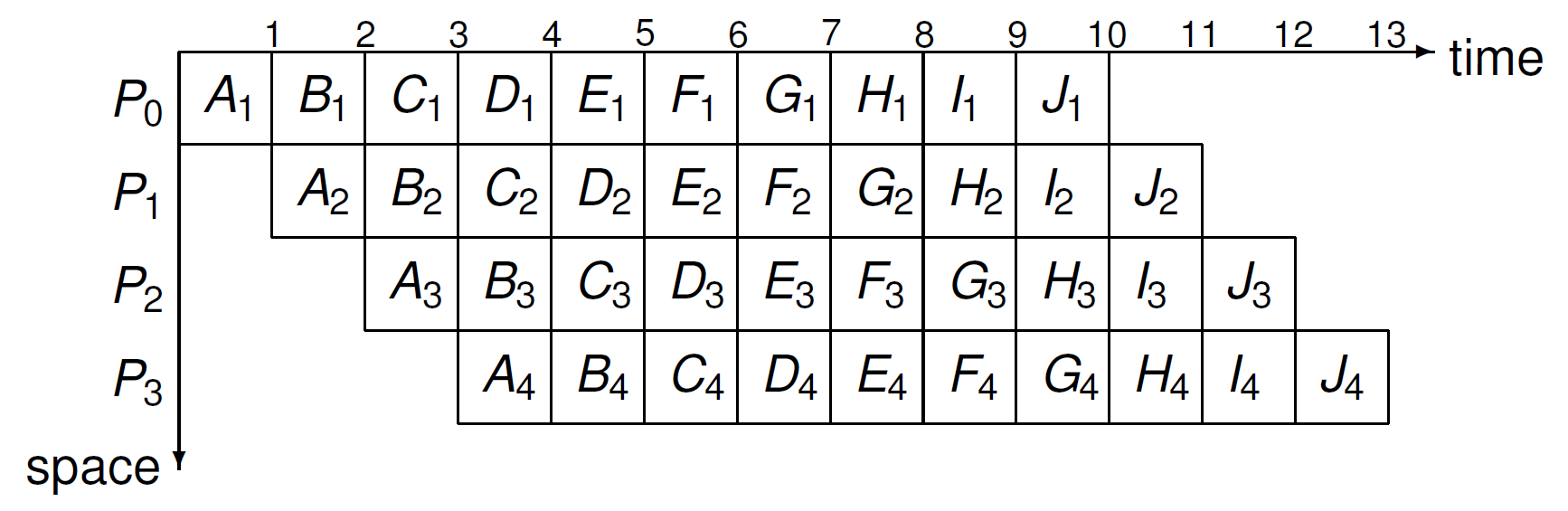
Fig. 155 The space diagram to produce 10 units \(A\), \(B\), \(C\), \(D\), \(E\), \(F\), \(G\), \(H\), \(I\), \(J\), with a pipeline of four processors \(P_0\), \(P_1\), \(P_2\), and \(P_3\).

Using the assumption that every stage requires the same amount of processing time, which is one time unit, we see that the parallel time is 13 time units, whereas the sequential time is \(4 \times 10 = 40\). So, the speedup is \(40/13 \approx 3.08\).

Registers and Shared Memory

Assume a CUDA kernel is launched with 8 thread blocks, with 512 threads in each block.

1. The kernel defines a local variable.

   How many copies of this variable exist during the execution of the kernel?

2. The kernel define a variable as shared memory.

   How many copies of this variable exist during the execution of the kernel?

Justify the number in your answer.

The answers to the two questions are below.

1. \(8 \times 512\) copies of the variable, because local variables are stored in registers, and each thread has its own registers.

2. 8 copies of the variable, because shared memory is shared between all threads in a block and because there are 8 blocks, there are 8 copies of the variable.

Convolutions

Consider the convolution of two power series given by coefficients in \(x\) and \(y\):

\[z_k = \sum_{i=0}^k x_i y_{k-1},\]

where \(z_k\) is a coefficient of the series \(z_0 + z_1 t + z_2 t^2 + \cdots\).

A basic implementation is given in the kernel below:

__global__ void convolute
( double *x, double *y, double *z )
{
   int k = threadIdx.x;     // thread k computes z[k]
   z[k] = x[0]*y[k];
   for(int i=1; i<=k; i++) z[k] = z[k] + x[i]*y[k-i];
}

This kernel is called for one block of threads. You may assume that the number of threads in the block equals the dimension of the arrays \(x\), \(y\), and \(z\).

1. What is the Compute to Global Memory Access ratio for the kernel?

2. Change the kernel into an equivalent one using fewer global memory accesses.

3. What is the CGMA ratio for your new kernel?

4. Explain the thread divergence of the given kernel.

   Describe a way to eliminate the thread divergence.

The answers to those questions are below.

1. The CGMA ratio of the kernel is computed as follows.

   • z[k] = x[0]*y[k] does one multiplication and 3 memory accesses;

   • z[k] = z[k] + x[i]*y[k-i] does one addition, one multiplication, and 4 memory accesses.

   Therefore, the CGMA ratio is

   \[\frac{1}{3} + \frac{2 k}{4 k}\]

   for thread \(k\).

2. A new kernel with fewer memory accesses is below.

   __global__ void convolute
   ( double *x, double *y, double *z )
   {
      int k = threadIdx.x;   // thread k computes z[k]
      double zk;             // a register stores z[k]
      __shared__ xv[MAX];    // store x and y
      __shared__ yv[MAX];    // into shared memory
      xv[k] = x[k];          // assume dimension
      yv[k] = y[k];          // equals #threads
      __syncthreads;
      zk = xv[0]*yv[k];
      for(int i=1; i<=k; i++) zk = zk + xv[i]*yv[k-i];
      z[k] = zk;
   }
   

3. The CGMA ratio of this new kernel is \(\displaystyle \frac{1 + 2 k}{3}\).

4. The new kernel, and the original kernel as well, has thread divergence, because of the test i<=k, each thread does a different number of operations.

   Because all threads in a warp execute the same instruction, executing this kernel will require twice the blockDim.x.

   Zero padding eliminates thread divergence, as in the kernel below.

   __global__ void convolute
   ( double *x, double *y, double *z )
   {
      int k = threadIdx.x;   // thread k computes z[k]
      int dim = blockDim.x;
      double zk;             // a register stores z[k]
      __shared__ xv[MAX];    // store x and y
      __shared__ yv[2*MAX];  // into shared memory
      xv[k] = x[k];          // assume dimension
      yv[k] = 0.0;
      yv[k] = y[dim+k];      // equals #threads
      __syncthreads;
      zk = xv[0]*yv[dim+k];
      for(int i=1; i<=dim; i++)
         zk = zk + xv[i]*yv[k+dim-i];
      z[k] = zk;
   }