Fall 2024 Final Exam Questions

The six questions below appeared on the final exam of Fall 2024.

Question 1 : Isoefficiency

Let \(\displaystyle T(n,p) = n \log(p) + \frac{n^2}{p}\) be the time of a parallel program to process \(n\) items with \(p\) processors.

  1. Compute the efficiency for \(n = 1000\) and \(p = 8\).

  2. If we want an efficiency of at least 90% for \(p = 128\), what should then the value for \(n\) be?

Below is a possible solution.

  1. Efficiency is speedup divided by the number of processors \(p\).

    \[S(n,p) = \frac{n^2}{(n \log(p) + n^2/p}, \quad E(n,p) = \frac{S(n,p)}{p}.\]

    evaluated at \(n = 1000\), \(p = 8\): \(E(1000, 8) = 0.98\) or 98%.

    Observe that the 2-logarithm is used.

  2. For a 90% efficiency with p = 128, we solve

\[(1/128) n^2/(n \log(128) + n^2/128) = 0.9,\]

or equivalently

\[n^2 = 128 \times 0.9 (7 n + n^2/128) = 128 \times 0.9 \times 7 n + 0.9 n^2\]

which simplifies further into \(0.1 n^2 = 128 \times 0.9 \times 7n\), and \(0.1 n = 128 \times 0.9 \times 7\), leading to

\[n = 128 \times 9 \times 7 = 8064.\]

So, we need a dimension of 8,064 to obtain a 90% efficiency with 128 processors.

Using the 10-logarithm instead gives 5590.

Question 2 : Multitasked Radix Sort

Describe the application of tasking for a parallel radix sort for floating-point numbers, considering the first \(k\) bits of the fraction of the floats and using \(p = 2^k\) tasks. Task \(t\) maintains the sorted sequence of all numbers where the first \(k\) bits equals \(t\). For example, if \(k = 2\), then the buckets are 00, 01, 10, 11, corresponding to the first bits in the fraction of the numbers.

What is the expected speedup? Justify your answer.

Below is a possible solution.

  • Sorting \(n\) numbers has a cost of \(O(n \log(n))\).

  • With \(p\) processors and \(p\) buckets, separating the numbers into the buckets takes \(O(n)\) sequential time, which is divided by \(p\) when done in parallel.

  • Assuming the buckets hold each about \(n/p\) numbers, sorting the buckets takes \(O((n/p) \log(n/p))\) time.

Therefore, the expected speedup is

\[\frac{n \log(n)}{\frac{n}{p} \log \left( \frac{n}{p} \right)}.\]

Question 3 : Divide-and-Conquer Polynomial Evaluation

Design a divide-and-conquer parallel program to evaluate

\[p(x) = c_0 + c_1 x + c_2 x^2 + \cdots + c_d x^d, \quad d = 2^n,\]

at some \(x\), for fixed coefficients \(c_0\), \(c_1\), \(c_2\), \(\cdots\), \(c_d\).

  1. What is the task graph for this parallel program?

  2. Given sufficiently many processors, use the task graph to derive the best speedup for this problem.

A possible solution is below.

The base case of the recursion is for \(n=0\), or \(d=1\).

In each step of the recursion, the polynomial is split in two (almost) equal halves:

\[p(x) = p_1 + x^{d/2} p_2, \quad \deg(p_1) = \frac{d}{2} - 1, \quad \deg(p_2) = \frac{d}{2}.\]

  1. The task graph is a binary tree. For example, for \(d=4\).

    c0 + c1*x + c2*x^2 + c3*x^3 + c4*x^4

= (c0 + x*c1) + x^2*(c2 + c3*x + c4*x^2)

= (c0)  (c1)    x^2*(c2 + x*(c3 + c4*x))

=                (c2)   x*(c3 + x*c4)

=                       (c3)    (c4)

  2. The length of the critical path corresponds to the depth of the tree. Therefore, given sufficiently many processors, the parallel time is \(O(\log(d)\) whereas the sequential time is \(O(d)\), yielding a speedup proportional to \(d/\log(d)\).

Question 4 : Pipelined Function Evaluation

The problem is to evaluate \(\displaystyle f(x) = \sum_{k=1}^4 e^{-k x^2} \sin(kx)\) at \(x_1\), \(x_2\), \(\ldots\), \(x_{10}\).

  1. Define a 4-stage pipeline algorithm for this problem.

  2. Draw a space time diagram to compute the speedup.

Below is a possible solution.

  1. There are four terms in the sum of the definition of \(f\). Therefore, there are four stages, where \(i\) runs from 1 to 10 to evaluate \(f\) at \(x_1\), \(x_2\), \(\ldots\), \(x_{10}\).

    1. The first processor receives \(x_i\) as input, evaluates \(e^{- x^2} \sin(x)\) at \(x = x_i\), and sends it to the second processor.

    2. The seconds processor receives \(e^{- x_i^2} \sin(x_i)\), evaluates \(e^{-2 x^2} \sin(2x)\) at \(x = x_i\), and sends \(e^{- x_i^2} \sin(x_i) + e^{-2 x_i^2} \sin(2x_i)\) to the third processor.

    3. The third processor receives \(e^{- x_i^2} \sin(x_i) + e^{-2 x_i^2} \sin(2x_i)\), evaluates \(e^{-3 x^2} \sin(3x)\) at \(x = x_i\), and sends \(e^{- x_i^2} \sin(x_i) + e^{-2 x_i^2} \sin(2x_i) + e^{-3 x_i^2} \sin(3x_i)\) to the fourth processor.

    4. The third processor receives \(e^{- x_i^2} \sin(x_i) + e^{-2 x_i^2} \sin(2x_i) + e^{-3 x_i^2} \sin(3x_i)\), evaluates \(e^{-4 x^2} \sin(4x)\) at \(x = x_i\), and sends \(e^{- x_i^2} \sin(x_i) + e^{-2 x_i^2} \sin(2x_i) + e^{-3 x_i^2} \sin(3x_i) + e^{-4 x_i^2} \sin(4x_i)\) to the output.

  2. The space time diagram is shown in Fig. 156.

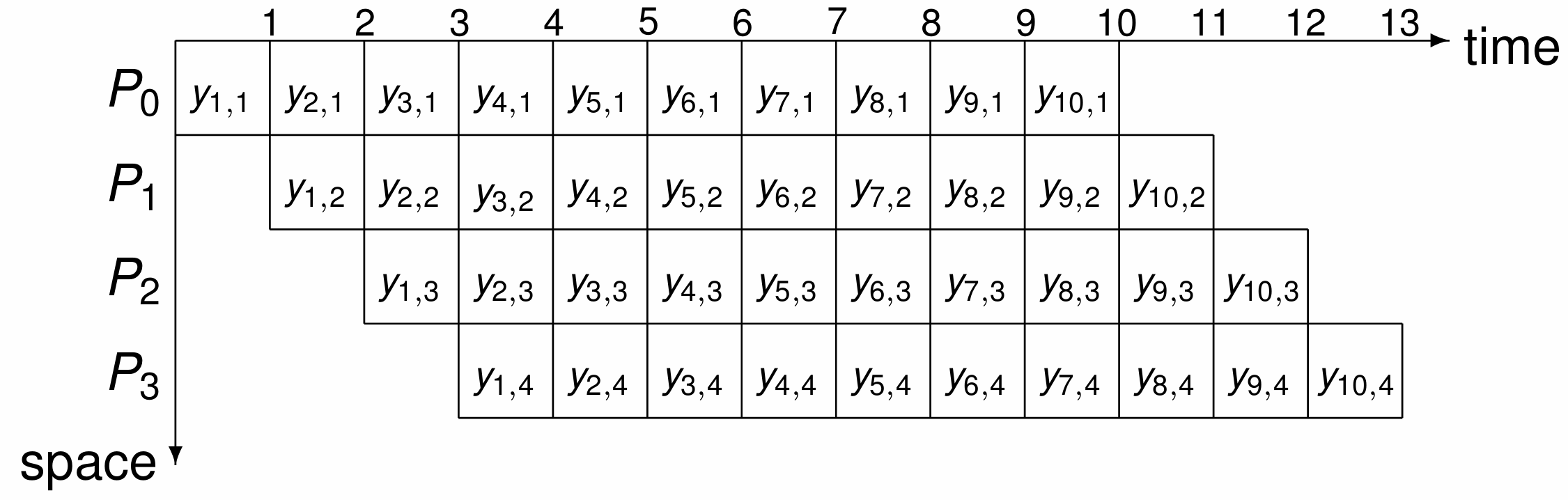
    _images/figspacetimefuneval.png

    Fig. 156 The space diagram to evaluate \(f\) at \(x_1\), \(x_2\), \(x_3\), \(x_4\), \(x_5\), \(x_6\), \(x_7\), \(x_8\), \(x_9\), \(x_{10}\), with a pipeline of four processors \(P_0\), \(P_1\), \(P_2\), and \(P_3\), where \(y_{i,j}\) is the output of stage \(j\) at \(x_i\).

    The space diagram in Fig. 156 allows to deduce the speedup of \(40/13\).

Question 5 : Data Staging

Consider the design of a kernel to compute the square of the differences between the coordinates of the first point and 32 other points in the plane. Given \((x_0, y_0)\), \((x_1, y_1)\), \(\ldots\), \((x_{32}, y_{32})\), the kernel computes

\[(x_0 - x_1)^2 + (x_0 - x_2)^2 + \cdots + (x_0 - x_{32})^2 + (y_0 - y_1)^2 + (y_0 - y_2)^2 + \cdots + (y_0 - y_{32})^2.\]

What is the best way to stage the input data,

  1. as \(x_0\), \(y_0\), \(x_1\), \(y_1\), \(\ldots\), \(x_{32}\), \(y_{32}\), or

  2. as \(x_0\), \(x_1\), \(\ldots\), \(x_{32}\), \(y_0\), \(y_1\), \(\ldots\), \(y_{32}\)?

Justify your answer.

Below is a possible solution.

For parallelism, thread \(i\) will compute \((x_0 - x_i)^2\), loading in \(x_0\) first and and then reading \(x_i\) from global memory. In the second stage, thread \(i\) loads y_0, then \(y_i\) to compute \((y_0 - y_i)^2\). The numbers \((x_0 - x_i)^2\) and \((y_0 - y_i)^2\) are stored in shared memory for the prefix sum algorithm.

If \(x_0\), \(x_1\), \(\ldots\), \(x_{32}\) are stored in adjacent locations in global memory, then adjacent threads will load data at adjacent locations which is beneficial for memory coalescing. The same argument holds for storing \(y_0\), \(y_1\), \(\ldots\), \(y_{32}\) in adjacent locations in global memory.

So, the second way of staging the input data works best.

Question 6 : Resource Limitations

An Ampere A100 GPU has 108 multiprocessors, with 64 cores per multiprocessor.

Per block, 65536 registers and 49152 bytes of shared memory are available, for a total of 167936 bytes of shared memory per multiprocessor. The maximum number of threads per block is 1024, and 2048 is the maximum number of threads for each multiprocessor.

  1. Kernel A uses 256 threads/block, 10 registers/thread, and 1024 bytes of shared memory/block.

  2. Kernel B uses 64 threads/block, 15 registers/thread, and 512 bytes of shared memory/block.

Can the kernels achieve full occupancy? If not, specify the limiting factor(s).

Below is a possible solution.

Both kernels are below the limit of 1024 threads per block.

Kernel A needs \(10 \times 256 = 2560\) registers, which is below the 65536 number of available registers. Each block uses 1024 bytes of shared memory, which is below the available number of bytes of shared memory per block, and at \(256/64 = 4\), the usage of shared memory per streaming multiprocessor is 4096, also below the available 167936 bytes per streaming multiprocessor. So, kernel A can achieve full occupancy.

Kernel B uses \(64 \times 15 = 960\) registers per block, which is below the limit of 65536. If 108 blocks are launched, then kernel B uses \(108 \times 512 = 55296\) bytes of shared memory, also below the available amount of shared memory. So, kernel B can achieve full occupancy.