Data Partitioning

To distribute the work load, we distinguish between functional and domain decomposition. To synchronize computations, we can use MPI_Barrier. We consider efficient scatter and gather implementations to fan out data and to fan in results. To overlap the communication with computation, we can use the nonblocking immediate send and receive operations.

functional and domain decomposition

To turn a sequential algorithm into a parallel one, we distinguish between functional and domain decomposition: In a functional decomposition, the arithmetical operations are distributed among several processors. The Monte Carlo simulations are example of a functional decomposition. In a domain decomposition, the data are distributed among several processors. The Mandelbrot set computation is an example of a domain decomposition. When solving problems, the entire data set is often too large to fit into the memory of one computer. Complete game trees (e.g.: the game of connect-4 or four in a row) consume an exponential amount of memory.

Divide and conquer used to solve problems:

  1. break the problem in smaller parts;
  2. solve the smaller parts; and
  3. assemble the partial solutions.

Often, divide and conquer is applied in a recursive setting where the smallest nontrivial problem is the base case. Sorting algorithms which apply divide and conquer are mergesort and quicksort.

parallel summation

Applying divide and conquer, we sum a sequence of numbers with divide and conquer, as in the following formula.

\[\begin{split}\begin{array}{lcr} {\displaystyle \sum_{k=0}^7 x_k} & = & (x_0 + x_1 + x_2 + x_3) + (x_4 + x_5 + x_6 + x_7) \\ & = & ((x_0 + x_1) + (x_2 + x_3)) + ((x_4 + x_5) + (x_6 + x_7)) \end{array}\end{split}\]

The grouping of the summands in pairs is shown in Fig. 23.

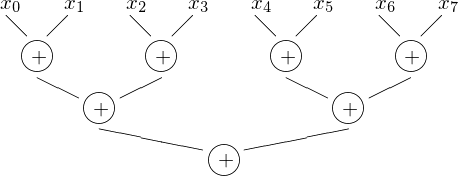
_images/figsumdivconq.png

Fig. 23 With 4 processors, the summation of 8 numbers in done in 3 steps.

The size of the problem is n, where \(\displaystyle S = \sum_{k=0}^{n-1} x_k\). Assume we have 8 processors to make 8 partial sums:

\[\begin{split}\begin{array}{lcr} S & = & (S_0 + S_1 + S_2 + S_3) + (S_4 + S_5 + S_6 + S_7) \\ & = & ((S_0 + S_1) + (S_2 + S_3)) + ((S_4 + S_5) + (S_6 + S_7)) \end{array}\end{split}\]

where \(m = (n-1)/8\) and \(\displaystyle S_i = \sum_{k=0}^{m} x_{k + im}\) The communication pattern goes along divide and conquer:

  1. the numbers \(x_k\) are scattered in a fan out fashion,
  2. summing the partial sums happens in a fan in mode.

Fanning out an array of data is shown in Fig. 24.

_images/figfanoutdata.png

Fig. 24 Fanning out data.

Algorithm: at step k, 2**k processors have data, and execute:
for j from 0 to 2**(k-1) do
    processor j sends data/2**(k+1) to processor j + 2**k;
    processor j+2**k receives data/2**(k+1) from processor j.

In fanning out, we use the same array for all nodes, and use only one send/recv statement. Observe the bit patterns in nodes and data locations, as shown in Table 8.

Table 8 Bit patterns and data locations.
  step
node 0 1 2 3 data
000 [0...7] [0...3] [0...1] [0] 000
001   [4...7] [4...5] [4] 100
010     [2...3] [2] 010
011     [6...7] [6] 110
100       [1] 001
101       [5] 101
110       [3] 011
111       [7] 111

At step 3, the node with label in binary expansion \(b2 b1 b0\) has data starting at index \(b_0 b_1 b_2\).

Fanning out with MPI is illustrated below, with 8 processes.

$ mpirun -np 8 /tmp/fan_out_integers
stage 0, d = 1 :
0 sends 40 integers to 1 at 40, start 40
1 received 40 integers from 0 at 40, start 40
stage 1, d = 2 :
0 sends 20 integers to 2 at 20, start 20
1 sends 20 integers to 3 at 60, start 60
2 received 20 integers from 0 at 20, start 20
3 received 20 integers from 1 at 60, start 60
stage 2, d = 4 :
0 sends 10 integers to 4 at 10, start 10
1 sends 10 integers to 5 at 50, start 50
2 sends 10 integers to 6 at 30, start 30
3 sends 10 integers to 7 at 70, start 70
4 received 10 integers from 0 at 10, start 10
6 received 10 integers from 2 at 30, start 30
7 received 10 integers from 3 at 70, start 70
data at all nodes :
5 received 10 integers from 1 at 50, start 50
2 has 10 integers starting at 20 with 20, 21, 22
7 has 10 integers starting at 70 with 70, 71, 72
0 has 10 integers starting at 0 with 0, 1, 2
1 has 10 integers starting at 40 with 40, 41, 42
3 has 10 integers starting at 60 with 60, 61, 62
4 has 10 integers starting at 10 with 10, 11, 12
6 has 10 integers starting at 30 with 30, 31, 32
5 has 10 integers starting at 50 with 50, 51, 52

To synchronize across all members of a group we apply MPI_Barrier(comm) where comm is the communicator (``MPI_COMM_WORLD). MPI_Barrier blocks the caller until all group members have called the statement. The call returns at any process only after all group members have entered the call.

The computation of the offset is done by the function parity_offset, as used in the program to fan out integers.

int parity_offset ( int n, int s );
/* returns the offset of node with label n
 * for data of size s based on parity of n */

int parity_offset ( int n, int s )
{
   int offset = 0;
   s = s/2;
   while(n > 0)
   {
      int d = n % 2;
      if(d > 0) offset += s;
      n = n/2;
      s = s/2;
   }
   return offset;
}

The main program to fan out integers is below.

int main ( int argc, char *argv[] )
{
   int myid,p,s,i,j,d,b;
   int A[size];

   MPI_Status status;
   MPI_Init(&argc,&argv);
   MPI_Comm_size(MPI_COMM_WORLD,&p);
   MPI_Comm_rank(MPI_COMM_WORLD,&myid);

   if(myid == 0) /* manager initializes */
      for(i=0; i<size; i++) A[i] = i;

   s = size;
   for(i=0,d=1; i<3; i++,d*=2) /* A is fanned out */
   {
      s = s/2;
      if(v>0) MPI_Barrier(MPI_COMM_WORLD);
      if(myid == 0) if(v > 0) printf("stage %d, d = %d :\n",i,d);
      if(v>0) MPI_Barrier(MPI_COMM_WORLD);
      for(j=0; j<d; j++)
      {
         b = parity_offset(myid,size);
         if(myid == j)
         {
            if(v>0) printf("%d sends %d integers to %d at %d, start %d\n",
                           j,s,j+d,b+s,A[b+s]);
            MPI_Send(&A[b+s],s,MPI_INT,j+d,tag,MPI_COMM_WORLD);
         }
         else if(myid == j+d)
         {
            MPI_Recv(&A[b],s,MPI_INT,j,tag,MPI_COMM_WORLD,&status);
            if(v>0)
               printf("%d received %d integers from %d at %d, start %d\n",
                      j+d,s,j,b,A[b]);
         }
      }
   }
   if(v > 0) MPI_Barrier(MPI_COMM_WORLD);
   if(v > 0) if(myid == 0) printf("data at all nodes :\n");
   if(v > 0) MPI_Barrier(MPI_COMM_WORLD);
   printf("%d has %d integers starting at %d with %d, %d, %d\n",
          myid,size/p,b,A[b],A[b+1],A[b+2]);
   MPI_Finalize();
   return 0;
}

Fanning in the results is illustrated in Fig. 25.

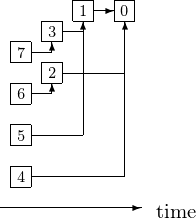
_images/figfaninresults.png

Fig. 25 Fanning in results.

Algorithm: at step k, 2**k processors send results and execute:
for j from 0 to 2**k-1 do
    processor j+2**k sends the result to processor j;
    processor j receives the result from processor j+2**k.

We run the algorithm for decreasing values of k: for example: k=2,1,0.

An Application

Computing \(\pi\) to trillions of digits is a benchmark problem for supercomputers.

One of the remarkable discoveries made by the PSLQ Algorithm (PSLQ = Partial Sum of Least Squares, or integer relation detection) is a simple formula that allows to calculating any binary digit of \(\pi\) without calculating the digits preceding it:

\[\pi = \sum_{i=0}^\infty \frac{1}{16^i} \left( \frac{4}{8i+1} - \frac{2}{8i+4} - \frac{1}{8i+5} - \frac{1}{8i+6} \right).\]

BBP stands for Bailey, Borwein and Plouffe. Instead of adding numbers, we concatenate strings.

Some readings on calculations for $pi$ are listed below:

  • David H. Bailey, Peter B. Borwein and Simon Plouffe: On the Rapid Computation of Various Polylogarithmic Constants. Mathematics of Computation 66(218): 903–913, 1997.
  • David H. Bailey: the BBP Algorithm for Pi. September 17, 2006. <http://crd-legacy.lbl.gov/~dhbailey/dhbpapers/>
  • Daisuke Takahashi: Parallel implementation of multiple-precision arithmetic and 2, 576, 980, 370, 000 decimal digits of pi calculation. Parallel Computing 36(8): 439-448, 2010.

Nonblocking Point-to-Point Communication

The MPI_SEND and MPI_RECV are blocking:

  • The sender must wait till the message is received.
  • The receiver must wait till the message is sent.

For synchronized computations, this is desirable. To overlap the communication with the computation, we may prefer the use of nonblocking communication operations:

  • MPI_ISEND for the Immediate send; and
  • MPI_IRECV for the Immediate receive.

The status of the immediate send/receive

  • can be queried with MPI_TEST; or
  • we can wait for its completion with MPI_WAIT.

The specification of the MPI_ISEND command

MPI_ISEND(buf, count, datatype, dest, tag, comm, request)

is in Table 9.

Table 9 Specification of the MPI_ISEND command.
parameter description
buf address of the send buffer
count number of elements in send buffer
datatype datatype of each send buffer element
dest rank of the destination
tag message tag
comm communicator
request communication request (output)

The sender should not modify any part of the send buffer after a nonblocking send operation is called, until the send completes.

The specification of the MPI_IRECV command

MPI_IRECV(buf, count, datatype, source, tag, comm, request)

is in Table 10.

Table 10 Specification of the MPI_IRECV command.
parameter description
buf address of the receive buffer
count number of elements in receive buffer
datatype datatype of each receive buffer element
source rank of source or MPI_ANY_SOURCE
tag message tag or MPI_ANY_TAG
comm communicator
request communication request (output)

The receiver should not access any part of the receive buffer after a nonblocking receive operation is called, until the receive completes.

After the call to MPI_ISEND or MPI_IRECV, the request can be used to query the status of the communication or wait for its completion.

To wait for the completion of a nonblocking communication:

MPI_WAIT (request, status)

with specifications in Table 11.

Table 11 Specification of the MPI_WAIT command.
parameter description
request communication request
status status object

To test the status of the communication:

MPI_TEST (request, flag, status)

with specifications in Table 12.

Table 12 Specification of the MPI_TEST command.
parameter description
request communication request
flag true if operation completed
status status object

Exercises

  1. Adjust the fanning out of the array of integers so it works for any number \(p\) of processors where \(p = 2^k\) for some \(k\). You may take the size of the array as an integer multiple of \(p\). To illustrate your program, provide screen shots for \(p = 8, 16\), and 32.
  2. Complete the summation and the fanning in of the partial sums, extending the program. You may leave \(p = 8\).