Introduction to the Intel Threading Building Blocks¶
Instead of working directly with threads, we can define tasks that are then mapped to threads. Work stealing is an alternative to load balancing.
the Intel Threading Building Blocks (TBB)¶
In this week we introduce programming tools for shared memory parallelism. Today we introduce a third tool:
- OpenMP: programming shared memory parallel computers;
- Pthreads: POSIX standard for Unix system programming; and
- Intel Threading Building Blocks (TBB) for multicore processors.
The Intel TBB is a library that helps you leverage multicore performance without having to be a threading expert. The advantage of Intel TBB is that it works at a higher level than raw threads, yet does not require exotic languages or compilers. The library differs from others in the following ways: TBB enables you to specify logical parallelism instead of threads; TBB targets threading for performance; TBB is compatible with other threading packages; TBB emphasizes scalable, data parallel programming; TBB relies on generic programming, (e.g.: use of STL in C++). The code is open source, free to download at < http://threadingbuildingblocks.org/>
task based programming and work stealing¶
Tasks are much lighter than threads. On Linux, starting and terminating a task is about 18 times faster than starting and terminating a thread; and a thread has its own process id and own resources, whereas a task is typically a small routine. The TBB task scheduler uses work stealing for load balancing. In scheduling threads on processors, we distinguish between work sharing and work stealing. In work sharing, the scheduler attempts to migrate threads to under-utilized processors in order to distribute the work. In work stealing, under-utilized processors attempt to steal threads from other processors.
Our first C++ program, similar to our previous Hello world! programs,
using TBB is below.
A class in C++ is a like a struct in C
for holding data attributes and functions (called methods).
#include "tbb/tbb.h"
#include <cstdio>
using namespace tbb;
class say_hello
{
const char* id;
public:
say_hello(const char* s) : id(s) { }
void operator( ) ( ) const
{
printf("hello from task %s\n",id);
}
};
int main( )
{
task_group tg;
tg.run(say_hello("1")); // spawn 1st task and return
tg.run(say_hello("2")); // spawn 2nd task and return
tg.wait( ); // wait for tasks to complete
}
The run method spawns the task immediately,
but does not block the calling task, so control returns immediately.
To wait for the child tasks to finish,
the classing task calls wait.
Observe the syntactic simplicity of task_group.
When running the code, we see on screen:
$ ./hello_task_group
hello from task 2
hello from task 1
$
using the parallel_for¶
Consider the following problem of raising complex numbers to a large power.
- Input \(n \in {\mathbb Z}_{>0}, d \in {\mathbb Z}_{>0}\),
\({\bf x} \in {\mathbb C}^n\).
- Output \({\bf y} \in {\mathbb C}^n, y_k = x_k^d\),
for \(k=1,2,\ldots,n\).
the serial program¶
To avoid overflow, we take complex numbers on the unit circle.
In C++, complex numbers are defined as a template class.
To instantiate the class complex with the type double
we first declare the type dcmplx.
Random complex numbers are generated as
\(e^{2 \pi i \theta} = \cos(2 \pi \theta) + i \sin(2 \pi \theta)\),
for random \(\theta \in [0,1]\).
#include <complex>
#include <cstdlib>
#include <cmath>
using namespace std;
typedef complex<double> dcmplx;
dcmplx random_dcmplx ( void );
// generates a random complex number on the complex unit circle
dcmplx random_dcmplx ( void )
{
int r = rand();
double d = ((double) r)/RAND_MAX;
double e = 2*M_PI*d;
dcmplx c(cos(e),sin(e));
return c;
}
We next define the function to write arrays.
Observe the local declaration int i in the for loop,
the scientific formatting, and the methods real() and imag().
#include <iostream>
#include <iomanip>
void write_numbers ( int n, dcmplx *x ); // writes the array of n doubles in x
void write_numbers ( int n, dcmplx *x )
{
for(int i=0; i<n; i++)
cout << scientific << setprecision(4)
<< "x[" << i << "] = ( " << x[i].real()
<< " , " << x[i].imag() << ")\n";
}
Below it the prototype and the definition of the function
to raise an array of n double complex number to some power.
Because the builtin pow function applies repeated squaring,
it is too efficient for our purposes and we use a plain loop.
void compute_powers ( int n, dcmplx *x, dcmplx *y, int d );
// for arrays x and y of length n, on return y[i] equals x[i]**d
void compute_powers ( int n, dcmplx *x, dcmplx *y, int d )
{
for(int i=0; i < n; i++) // y[i] = pow(x[i],d); pow is too efficient
{
dcmplx r(1.0,0.0);
for(int j=0; j < d; j++) r = r*x[i];
y[i] = r;
}
}
Without command line arguments, the main program prompts the user for the number of elements in the array and for the power. The three command line arguments are the dimension, the power, and the verbose level. If the third parameter is zero, then no numbers are printed to screen, otherwise, if the third parameter is one, the powers of the random numbers are shown. Running the program in silent mode is useful for timing purposes. Below are some example sessions with the program.
$ /tmp/powers_serial
how many numbers ? 2
x[0] = ( -7.4316e-02 , 9.9723e-01)
x[1] = ( -9.0230e-01 , 4.3111e-01)
give the power : 3
x[0] = ( 2.2131e-01 , -9.7520e-01)
x[1] = ( -2.3152e-01 , 9.7283e-01)
$ /tmp/powers_serial 2 3 1
x[0] = ( -7.4316e-02 , 9.9723e-01)
x[1] = ( -9.0230e-01 , 4.3111e-01)
x[0] = ( 2.2131e-01 , -9.7520e-01)
x[1] = ( -2.3152e-01 , 9.7283e-01)
$ time /tmp/powers_serial 1000 1000000 0
real 0m17.456s
user 0m17.451s
sys 0m0.001s
The main program is listed below:
int main ( int argc, char *argv[] )
{
int v = 1; // verbose if > 0
if(argc > 3) v = atoi(argv[3]);
int dim; // get the dimension
if(argc > 1)
dim = atoi(argv[1]);
else
{
cout << "how many numbers ? ";
cin >> dim;
}
// fix the seed for comparisons
srand(20120203); //srand(time(0));
dcmplx r[dim];
for(int i=0; i<dim; i++)
r[i] = random_dcmplx();
if(v > 0) write_numbers(dim,r);
int deg; // get the degree
if(argc > 1)
deg = atoi(argv[2]);
else
{
cout << "give the power : ";
cin >> deg;
}
dcmplx s[dim];
compute_powers(dim,r,s,deg);
if(v > 0) write_numbers(dim,s);
return 0;
}
speeding up the computations with parallel_for¶
We first illustrate the speedup that can be obtained with a parallel version of the code.
$ time /tmp/powers_serial 1000 1000000 0
real 0m17.456s
user 0m17.451s
sys 0m0.001s
$ time /tmp/powers_tbb 1000 1000000 0
real 0m1.579s
user 0m18.540s
sys 0m0.010s
The speedup: \(\displaystyle \frac{17.456}{1.579} = 11.055\)
with 12 cores. The class ComputePowers is defined below
class ComputePowers
{
dcmplx *const c; // numbers on input
int d; // degree
dcmplx *result; // output
public:
ComputePowers(dcmplx x[], int deg, dcmplx y[])
: c(x), d(deg), result(y) { }
void operator()
( const blocked_range<size_t>& r ) const
{
for(size_t i=r.begin(); i!=r.end(); ++i)
{
dcmplx z(1.0,0.0);
for(int j=0; j < d; j++) z = z*c[i];
result[i] = z;
}
}
};
We next explain the use of tbb/blocked_range.h.
A blocked_range represents a half open range \([i,j)\)
that can be recursively split.
#include "tbb/blocked_range.h"
template<typename Value> class blocked_range
void operator()
( const blocked_range<size_t>& r ) const
{
for(size_t i=r.begin(); i!=r.end(); ++i)
{
Calling the parallel_for happens as follows:
#include "tbb/tbb.h"
#include "tbb/blocked_range.h"
#include "tbb/parallel_for.h"
#include "tbb/task_scheduler_init.h"
using namespace tbb;
Two lines change in the main program:
task_scheduler_init init(task_scheduler_init::automatic);
parallel_for(blocked_range<size_t>(0,dim),
ComputePowers(r,deg,s));
using the parallel_reduce¶
We consider the summation of integers as an application of work stealing. Fig. 28 and Fig. 29 are taken from the Intel TBB tutorial.
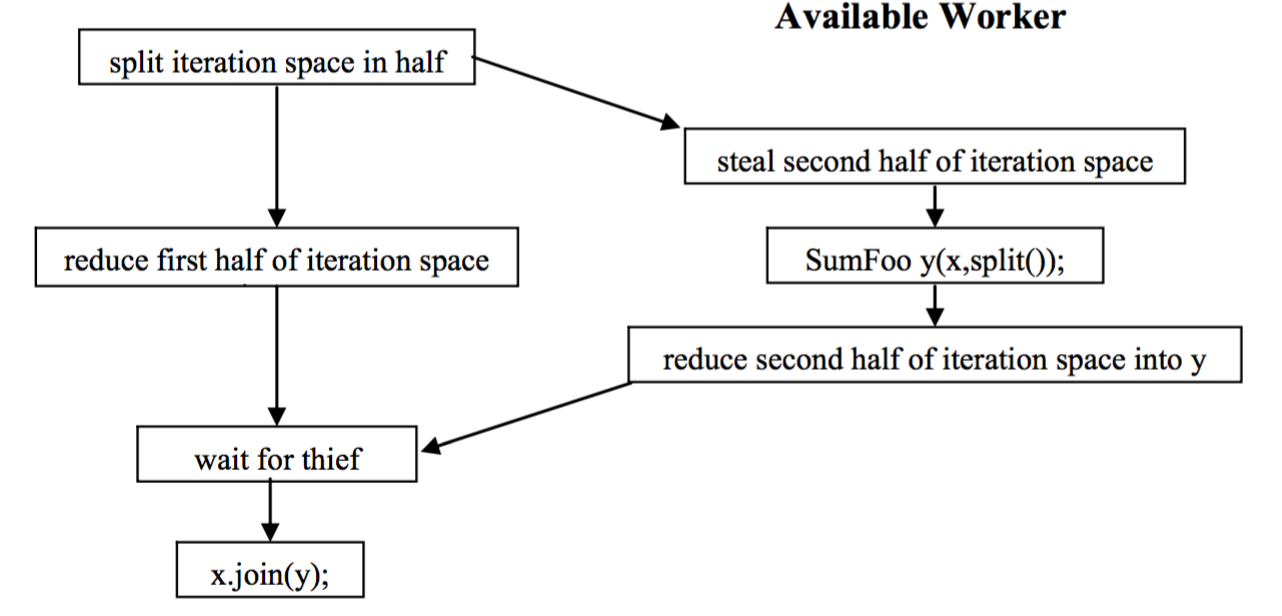
Fig. 28 An application of work stealing.

Fig. 29 What if no worker is available?
The definition of the class to sum a sequence of integers is below.
class SumIntegers
{
int *data;
public:
int sum;
SumIntegers ( int *d ) : data(d), sum(0) {}
void operator()
( const blocked_range<size_t>& r )
{
int s = sum; // must accumulate !
int *d = data;
size_t end = r.end();
for(size_t i=r.begin(); i != end; ++i)
s += d[i];
sum = s;
}
// the splitting constructor
SumIntegers ( SumIntegers& x, split ) :
data(x.data), sum(0) {}
// the join method does the merge
void join ( const SumIntegers& x ) { sum += x.sum; }
};
int ParallelSum ( int *x, size_t n )
{
SumIntegers S(x);
parallel_reduce(blocked_range<size_t>(0,n), S);
return S.sum;
}
The main program is below:
int main ( int argc, char *argv[] )
{
int n;
if(argc > 1)
n = atoi(argv[1]);
else
{
cout << "give n : ";
cin >> n;
}
int *d;
d = (int*)calloc(n,sizeof(int));
for(int i=0; i<n; i++) d[i] = i+1;
task_scheduler_init init
(task_scheduler_init::automatic);
int s = ParallelSum(d,n);
cout << "the sum is " << s
<< " and it should be " << n*(n+1)/2
<< endl;
return 0;
}
Bibliography¶
- Intel Threading Building Blocks. Tutorial. Available online via <http://www.intel.com>.
- Robert D. Blumofe and Charles E. Leiserson: Scheduling Multithreaded Computations by Work-Stealing. In the Proceedings of the 35th Annual IEEE Conference on Foundations of Computer Science (FoCS 1994), pages 356-368.
- Krste Asanovic, Ras Bodik, Bryan Christopher Catanzaro, Joseph James Gebis, Parry Husbands, Kurt Keutzer, David A. Patterson, William Lester Plishker, John Shalf, Samuel Webb Williams and Katherine A. Yelick: The Landscape of Parallel Computing Research: A View from Berkeley. Technical Report No. UCB/EECS-2006-183 EECS Department, University of California, Berkeley, December 18, 2006.
Exercises¶
- Modify the
hello world!program with so that the user is first prompted for a name. Two tasks are spawned and they use the given name in their greeting. - Modify
powers_tbb.cppso that the i*th entry is raised to the power *d-i. In this way not all entries require the same work load. Run the modified program and compare the speedup to check the performance of the automatic task scheduler.