Pipelined Computations

Although a process may consist in stages that have to be executed in order and thus there may not be much speedup possible for the processing of one item, arranging the stages in a pipeline speeds up the processing of many items.

Functional Decomposition

Car manufacturing is a successful application of pipelines. Consider a simplified car manufacturing process in three stages: (1) assemble exterior, (2) fix interior, and (3) paint and finish, as shown schematically Fig. 33.

Fig. 33 A schematic of a 3-stage pipeline at the left, with the corresponding space-time diagram at the right. After 3 time units, one car per time unit is completed. It takes 7 time units to complete 5 cars.

Definition of a Pipeline

A pipeline with p processors is a p-stage pipeline. A time unit is called a pipeline cycle. The time taken by the first p-1 cycles is the pipeline latency.

Suppose every process takes one time unit to complete. How long does it take till a p-stage pipeline completes n inputs? A p-stage pipeline on n inputs. After p time units the first input is done. Then, for the remaining \(n-1\) items, the pipeline completes at a rate of one item per time unit. So, it takes \(p + n-1\) time units for the p-stage pipeline to complete n inputs. The speedup S(p) for n inputs in a p-stage pipeline is thus

\[S(p) = \frac{n \times p}{p + n - 1}.\]

For a fixed number p of processors:

\[\lim_{n \rightarrow \infty} \frac{p \times n}{n + p - 1} = p.\]

Pipelining is a functional decomposition method to develop parallel programs. Recall the classification of Flynn: MISD = Multiple Instruction Single Data stream.

Another successful application of pipelining is floating-point addition. The parts of a floating-point number are shown in Fig. 34.

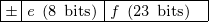
Fig. 34 A floating-point number has a sign bit, exponent, and fraction.

Adding to floats could be done in 6 cycles:

1. unpack fractions and exponents;
2. compare the exponents;
3. align the fractions;
4. add the fractions;
5. normalize the result; and
6. pack the fraction and the exponent of the result.

Adding two vectors of \(n\) floats with 6-stage pipeline takes \(n+6-1\) pipeline cycles, instead of \(6n\) cycles.

The functionality of the pipelines in Intel Core processors is shown in Fig. 35.

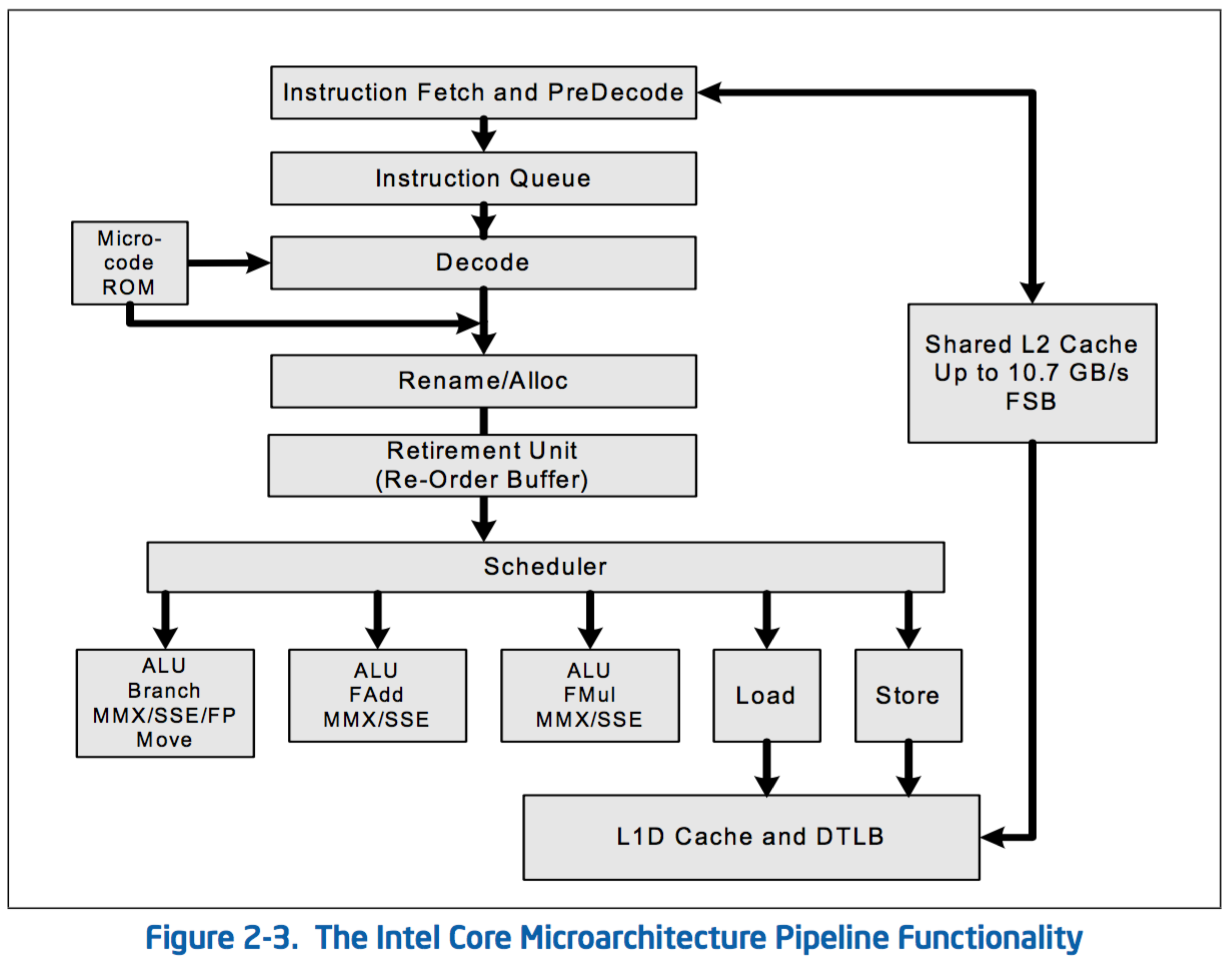
Fig. 35 Copied from the Intel Architecture Software Developer’s Manual.

Our third example of a successful application of pipelining is the denoising a signal. Every second we take 256 samples of a signal:

• \(P_1\): apply FFT,
• \(P_2\): remove low amplitudes, and
• \(P_3\): inverse FFT,

as shown in Fig. 36. Observe: the consumption of a signal is sequential.

Fig. 36 Pipeline to denoising a signal at the left, with space-diagram at the right.

Pipeline Implementations

A ring topology of processors is a natural way to implement a pipeline. In Fig. 37, the stages in a pipeline are performed by the processes organized in a ring.

Fig. 37 Four stages in a pipeline executed by four processes in a ring.

In a manager/worker organization, node 0 receives the input and sends it to node~1. Every node \(i\), for \(i= 1,2,\ldots,p-1\), does the following.

• It receives an item from node \(i-1\),
• performs operations on the item, and
• sends the processed item to node \((i+1) {\rm ~mod~} p\).

At the end of one cycle, node 0 has the output.

Using MPI to implement a pipeline

Consider the following calculation with \(p\) processes. Process 0 prompts the user for a number and sends it to process 1. For \(i > 0\): process \(i\) receives a number from process \(i-1\), doubles the number and sends it to process \(i \mbox{ mod } p\). A session of an MPI implementation of one pipeline cycle for this calculation shows the following:

$ mpirun -np 4 /tmp/pipe_ring
One pipeline cycle for repeated doubling.
Reading a number...
2
Node 0 sends 2 to the pipe...
Processor 1 receives 2 from node 0.
Processor 2 receives 4 from node 1.
Processor 3 receives 8 from node 2.
Node 0 received 16.
$

This example is a type 1 pipeline: efficient only if we have more than one instance to compute. The MPI code for the manager is below:

void manager ( int p )
/*
 * The manager prompts the user for a number and passes this number to node 1 for doubling.
 * The manager receives from node p-1 the result. */
{
   int n;
   MPI_Status status;

   printf("One pipeline cycle for repeated doubling.\n");
   printf("Reading a number...\n"); scanf("%d",&n);
   printf("Node 0 sends %d to the pipe...\n",n);
   fflush(stdout);
   MPI_Send(&n,1,MPI_INT,1,tag,MPI_COMM_WORLD);
   MPI_Recv(&n,1,MPI_INT,p-1,tag,MPI_COMM_WORLD,&status);
   printf("Node 0 received %d.\n",n);
}

Following is the MPI code for the workers.

void worker ( int p, int i )
/*
 * Worker with identification label i of p receives a number,
 * doubles it, and sends it to node i+1 mod p. */
{
   int n;
   MPI_Status status;

   MPI_Recv(&n,1,MPI_INT,i-1,tag,MPI_COMM_WORLD,&status);
   printf("Processor %d receives %d from node %d.\n",i,n,i-1);
   fflush(stdout);
   n *= 2;                      /* double the number */
   if(i < p-1)
      MPI_Send(&n,1,MPI_INT,i+1,tag,MPI_COMM_WORLD);
   else
      MPI_Send(&n,1,MPI_INT,0,tag,MPI_COMM_WORLD);
}

pipelined addition

Consider 4 processors in a ring topology as in Fig. 37. To add a sequence of 32 numbers, with data partitioning:

\[\underbrace{a_0, a_1, \ldots, a_7}_{\displaystyle A_k = \sum_{j=0}^k a_j}, \underbrace{b_0, b_1, \ldots, b_7}_{\displaystyle B_k = \sum_{j=0}^k b_j}, \underbrace{c_0, c_1, \ldots, c_7}_{\displaystyle C_k = \sum_{j=0}^k c_j}, \underbrace{d_0, d_1, \ldots, d_7}_{\displaystyle D_k = \sum_{j=0}^k d_j}.\]

The final sum is \(S = A_7 + B_7 + C_7 + D_7\). Fig. 38 shows the space-time diagram for pipeline addition.

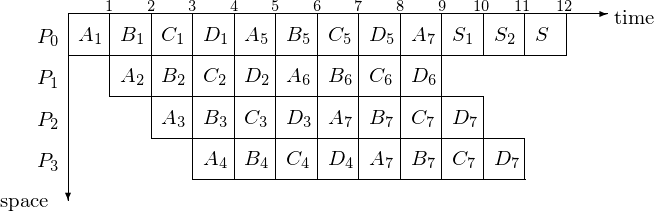
Fig. 38 Space-time diagram for pipelined addition, where \(S_1 = A_7 + B_7, S_2 = S_1 + C_7, S = S_2 + D_7\).

Let us compute the speedup for this pipelined addition. We finished addition of 32 numbers in 12 cycles: 12 = 32/4 + 4. In general, with p-stage pipeline to add n numbers:

\[S(p) = \frac{n-1}{\displaystyle \frac{n}{p} + p}\]

For fixed p: \(\displaystyle \lim_{n \rightarrow \infty} S(p) = p\).

A pipelined addition implemented with MPI using 5-stage pipeline shows the following on screen:

mpirun -np 5 /tmp/pipe_sum
The data to sum :  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Manager starts pipeline for sequence 0...
Processor 1 receives sequence 0 :  3 3 4 5 6
Processor 2 receives sequence 0 :  6 4 5 6
Processor 3 receives sequence 0 :  10 5 6
Processor 4 receives sequence 0 :  15 6
Manager received sum 21.
Manager starts pipeline for sequence 1...
Processor 1 receives sequence 1 :  15 9 10 11 12
Processor 2 receives sequence 1 :  24 10 11 12
Processor 3 receives sequence 1 :  34 11 12
Processor 4 receives sequence 1 :  45 12
Manager received sum 57.
Manager starts pipeline for sequence 2...
Processor 1 receives sequence 2 :  27 15 16 17 18
Processor 2 receives sequence 2 :  42 16 17 18
Processor 3 receives sequence 2 :  58 17 18
Processor 4 receives sequence 2 :  75 18
Manager received sum 93.
Manager starts pipeline for sequence 3...
Processor 1 receives sequence 3 :  39 21 22 23 24
Processor 2 receives sequence 3 :  60 22 23 24
Processor 3 receives sequence 3 :  82 23 24
Processor 4 receives sequence 3 :  105 24
Manager received sum 129.
Manager starts pipeline for sequence 4...
Processor 1 receives sequence 4 :  51 27 28 29 30
Processor 2 receives sequence 4 :  78 28 29 30
Processor 3 receives sequence 4 :  106 29 30
Processor 4 receives sequence 4 :  135 30
Manager received sum 165.
The total sum : 465
$

The MPI code is defined in the function below.

void pipeline_sum ( int i, int p ) /* performs a pipeline sum of p*(p+1) numbers */
{
   int n[p][p-i+1];
   int j,k;
   MPI_Status status;

   if(i==0)  /* manager generates numbers */
   {
      for(j=0; j<p; j++)
         for(k=0; k<p+1; k++) n[j][k] = (p+1)*j+k+1;
      if(v>0)
      {
         printf("The data to sum : ");
         for(j=0; j<p; j++)
            for(k=0; k<p+1; k++) printf(" %d",n[j][k]);
         printf("\n");
      }
   }
   for(j=0; j<p; j++)
      if(i==0)  /* manager starts pipeline of j-th sequence */
      {
         n[j][1] += n[j][0];
         printf("Manager starts pipeline for sequence %d...\n",j);
         MPI_Send(&n[j][1],p,MPI_INT,1,tag,MPI_COMM_WORLD);
         MPI_Recv(&n[j][0],1,MPI_INT,p-1,tag,MPI_COMM_WORLD,&status);
         printf("Manager received sum %d.\n",n[j][0]);
      }
      else      /* worker i receives p-i+1 numbers */
      {
         MPI_Recv(&n[j][0],p-i+1,MPI_INT,i-1,tag,MPI_COMM_WORLD,&status);
         printf("Processor %d receives sequence %d : ",i,j);
         for(k=0; k<p-i+1; k++) printf(" %d", n[j][k]);
         printf("\n");
         n[j][1] += n[j][0];
         if(i < p-1)
            MPI_Send(&n[j][1],p-i,MPI_INT,i+1,tag,MPI_COMM_WORLD);
         else
            MPI_Send(&n[j][1],1,MPI_INT,0,tag,MPI_COMM_WORLD);
      }
   if(i==0)  /* manager computes the total sum */
   {
      for(j=1; j<p; j++) n[0][0] += n[j][0];
      printf("The total sum : %d\n",n[0][0]);
   }
}

Exercises

1. Describe the application of pipelining technique for grading n copies of an exam that has p questions. Explain the stages and make a space-time diagram.
2. Write code to use the 4-stage pipeline to double numbers for a sequence of 10 consecutive numbers starting at 2.
3. Consider the evaluation of a polynomial \(f(x)\) of degree \(d\) given by its coefficient vector \((a_0,a_1,a_2,\ldots,a_d)\), using Horner’s method, e.g., for \(d=4\): \(f(x) = ((( a_4 x + a_3 ) x + a_2 )x + a_1 ) x + a_0\). Give MPI code of this algorithm to evaluate \(f\) at a sequence of n values for x by a p-stage pipeline.