Pipelined Sorting¶
We continue our study of pipelined computations, but now for shared memory parallel computers. The Intel Threading Building Blocks provide support for pipeline patterns.
Pipelines with Intel Threading Building Blocks (TBB)¶
The Intel Threading Building Blocks (TBB) classes pipeline
and filter implement the pipeline pattern.
A 3-stage pipeline is shown in Fig. 39.
Fig. 39 A 3-stage pipeline.
A session with a program using the Intel TBB goes as follows:
$ /tmp/pipe_tbb
the input sequence : 1 -2 3 -4
the output sequence : 8 -16 24 -32
$
The makefile contains
TBB_ROOT = /usr/local/tbb40_20131118oss
pipe_tbb:
g++ -I$(TBB_ROOT)/include -L$(TBB_ROOT)/lib \
pipe_tbb.cpp -o /tmp/pipe_tbb -ltbb
and pipe_tbb.cpp starts with
#include <iostream>
#include "tbb/pipeline.h"
#include "tbb/compat/thread"
#include "tbb/task_scheduler_init.h"
using namespace tbb;
int Sequence[] = {1,-2,3,-4,0}; // 0 is sentinel
The inheriting from the filter class is done as below:
class DoublingFilter: public filter {
int* my_ptr;
public:
DoublingFilter() :
filter(serial_in_order), my_ptr(Sequence) {}
// process items one at a time in the given order
void* operator()(void*) {
if(*my_ptr) {
*my_ptr = (*my_ptr)*2; // double item
return (void*)my_ptr++; // pass to next filter
}
else
return NULL;
}
};
A thread_bound_filter is a filter explicitly serviced
by a particular thread, in this case the main thread:
class OutputFilter: public thread_bound_filter
{
public:
OutputFilter() :
thread_bound_filter(serial_in_order) {}
void* operator()(void* item)
{
int *v = (int*)item;
std::cout << " " << (*v)*2;
return NULL;
}
};
The argument of run is the maximum number of live tokens.
void RunPipeline ( pipeline* p )
{
p->run(8);
}
The pipeline runs until the first filter returns NULL
and each subsequent filter has processed all items from its predecessor.
In the function main():
// another thread initiates execution of the pipeline
std::thread t(RunPipeline,&p);
The creation of a pipeline in the main program happens as follows:
int main ( int argc, char* argv[] )
{
std::cout << " the input sequence :";
for(int* s = Sequence; (*s); s++)
std::cout << " " << *s;
std::cout << "\nthe output sequence :";
DoublingFilter f; // construct the pipeline
DoublingFilter g;
OutputFilter h;
pipeline p;
p.add_filter(f); p.add_filter(g); p.add_filter(h);
// another thread initiates execution of the pipeline
std::thread t(RunPipeline,&p);
// process the thread_bound_filter
// with the current thread
while(h.process_item()
!= thread_bound_filter::end_of_stream)
continue;
// wait for pipeline to finish on the other thread
t.join();
std::cout << "\n";
return 0;
}
Sorting Numbers¶
We consider a parallel version of insertion sort,
sorting p numbers with p processors.
Processor i does p-i steps in the algorithm:
for step 0 to p-i-1 do
manager receives number
worker i receives number from i-1
if step = 0 then
initialize the smaller number
else if number > smaller number then
send number to i+1
else
send smaller number to i+1;
assign number to smaller number;
end if;
end for.
A pipeline session with MPI can go as below.
$ mpirun -np 4 /tmp/pipe_sort
The 4 numbers to sort : 24 19 25 66
Manager gets 24.
Manager gets 19.
Node 0 sends 24 to 1.
Manager gets 25.
Node 0 sends 25 to 1.
Manager gets 66.
Node 0 sends 66 to 1.
Node 1 receives 24.
Node 1 receives 25.
Node 1 sends 25 to 2.
Node 1 receives 66.
Node 1 sends 66 to 2.
Node 2 receives 25.
Node 2 receives 66.
Node 2 sends 66 to 3.
Node 3 receives 66.
The sorted sequence : 19 24 25 66
MPI code for a pipeline version of insertion sort is in
the program pipe_sort.c below:
int main ( int argc, char *argv[] )
{
int i,p,*n,j,g,s;
MPI_Status status;
MPI_Init(&argc,&argv);
MPI_Comm_size(MPI_COMM_WORLD,&p);
MPI_Comm_rank(MPI_COMM_WORLD,&i);
if(i==0) /* manager generates p random numbers */
{
n = (int*)calloc(p,sizeof(int));
srand(time(NULL));
for(j=0; j<p; j++) n[j] = rand() % 100;
if(v>0)
{
printf("The %d numbers to sort : ",p);
for(j=0; j<p; j++) printf(" %d", n[j]);
printf("\n"); fflush(stdout);
}
}
for(j=0; j<p-i; j++) /* processor i performs p-i steps */
if(i==0)
{
g = n[j];
if(v>0) { printf("Manager gets %d.\n",n[j]); fflush(stdout); }
Compare_and_Send(i,j,&s,&g);
}
else
{
MPI_Recv(&g,1,MPI_INT,i-1,tag,MPI_COMM_WORLD,&status);
if(v>0) { printf("Node %d receives %d.\n",i,g); fflush(stdout); }
Compare_and_Send(i,j,&s,&g);
}
MPI_Barrier(MPI_COMM_WORLD); /* to synchronize for printing */
Collect_Sorted_Sequence(i,p,s,n);
MPI_Finalize();
return 0;
}
The function Compare_and_Send is defined next.
void Compare_and_Send ( int myid, int step, int *smaller, int *gotten )
/* Processor "myid" initializes smaller with gotten at step zero,
* or compares smaller to gotten and sends the larger number through. */
{
if(step==0)
*smaller = *gotten;
else
if(*gotten > *smaller)
{
MPI_Send(gotten,1,MPI_INT,myid+1,tag,MPI_COMM_WORLD);
if(v>0)
{
printf("Node %d sends %d to %d.\n",
myid,*gotten,myid+1);
fflush(stdout);
}
}
else
{
MPI_Send(smaller,1,MPI_INT,myid+1,tag,
MPI_COMM_WORLD);
if(v>0)
{
printf("Node %d sends %d to %d.\n",
myid,*smaller,myid+1);
fflush(stdout);
}
*smaller = *gotten;
}
}
The function Collect_Sorted_Sequence follows:
void Collect_Sorted_Sequence ( int myid, int p, int smaller, int *sorted )
/* Processor "myid" sends its smaller number to the manager who collects
* the sorted numbers in the sorted array, which is then printed. */
{
MPI_Status status;
int k;
if(myid==0) {
sorted[0] = smaller;
for(k=1; k<p; k++)
MPI_Recv(&sorted[k],1,MPI_INT,k,tag,
MPI_COMM_WORLD,&status);
printf("The sorted sequence : ");
for(k=0; k<p; k++) printf(" %d",sorted[k]);
printf("\n");
}
else
MPI_Send(&smaller,1,MPI_INT,0,tag,MPI_COMM_WORLD);
}
Prime Number Generation¶
The sieve of Erathostenes is shown in Fig. 40.
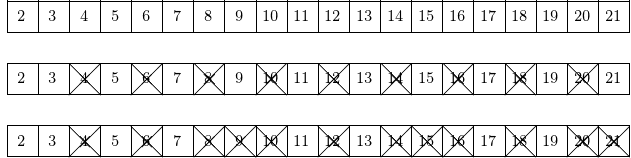
Fig. 40 Wiping out all multiples of 2 and 3 gives all prime numbers between 2 and 21.
A pipelined sieve algorithm is defined as follows. One stage in the pipeline
- receives a prime,
- receives a sequence of numbers,
- extracts from the sequence all multiples of the prime, and
- sends the filtered list to the next stage.
This pipeline algorithm is of type 2. As in type 1, multiple input items are needed for speedup; but the amount of work in every stage will complete fewer steps than in the preceding stage.
For example, consider a 2-stage pipeline to compute all primes \(\leq 21\) with the sieve algorithm:
- wipe out all multiples of 2, in nine multiplications;
- wipe out all multiples of 3, in five multiplications.
Although the second stage in the pipeline starts only after we determined that 3 is not a multiple of 2, there are fewer multiplications in the second stage. The space-time diagram with the multiplications is in Fig. 41.
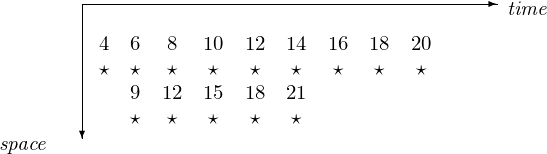
Fig. 41 A 2-stage pipeline to compute all primes \(\leq 21\).
A parallel implementation of the sieve of Erathostenes
is in the examples collection of the Intel TBB distribution,
in /usr/local/tbb40_20131118oss/examples/parallel_reduce/primes.
Computations on a 16-core computer kepler:
$ make
g++ -O2 -DNDEBUG -o primes main.cpp primes.cpp -ltbb -lrt
./primes
#primes from [2..100000000] = 5761455 (0.106599 sec with serial code)
#primes from [2..100000000] = 5761455 (0.115669 sec with 1-way parallelism)
#primes from [2..100000000] = 5761455 (0.059511 sec with 2-way parallelism)
#primes from [2..100000000] = 5761455 (0.0393051 sec with 3-way parallelism)
#primes from [2..100000000] = 5761455 (0.0287207 sec with 4-way parallelism)
#primes from [2..100000000] = 5761455 (0.0237532 sec with 5-way parallelism)
#primes from [2..100000000] = 5761455 (0.0198929 sec with 6-way parallelism)
#primes from [2..100000000] = 5761455 (0.0175456 sec with 7-way parallelism)
#primes from [2..100000000] = 5761455 (0.0168987 sec with 8-way parallelism)
#primes from [2..100000000] = 5761455 (0.0127005 sec with 10-way parallelism)
#primes from [2..100000000] = 5761455 (0.0116965 sec with 12-way parallelism)
#primes from [2..100000000] = 5761455 (0.0104559 sec with 14-way parallelism)
#primes from [2..100000000] = 5761455 (0.0109771 sec with 16-way parallelism)
#primes from [2..100000000] = 5761455 (0.00953452 sec with 20-way parallelism)
#primes from [2..100000000] = 5761455 (0.0111944 sec with 24-way parallelism)
#primes from [2..100000000] = 5761455 (0.0107475 sec with 28-way parallelism)
#primes from [2..100000000] = 5761455 (0.0151389 sec with 32-way parallelism)
elapsed time : 0.520726 seconds
$
Exercises¶
- Consider the evaluation of a polynomial \(f(x)\) of degree \(d\) given by its coefficient vector \((a_0,a_1,a_2,\ldots,a_d)\), using Horner’s method, e.g., for \(d=4\): \(f(x) = ((( a_4 x + a_3 ) x + a_2 )x + a_1 ) x + a_0\). Give code of this algorithm to evaluate \(f\) at a sequence of \(n\) values for \(x\) by a p-stage pipeline, using the Intel TBB.
- Write a pipeline with the Intel TBB to implement the parallel version of insertion sort we have done with MPI.
- Use Pthreads to implement the parallel version of insertion sort we have done with MPI.