Barriers for Synchronizations¶

For message passing, we distinguish between a linear, a tree, and a butterfly barrier. We end with a simple illustration of barriers with Pthreads.

Synchronizing Computations¶

A barrier has two phases. The arrival or trapping phase is followed by the departure or release phase. The manager maintains a counter: only when all workers have sent to the manager, does the manager send messages to all workers. Pseudo code for a linear barrier in a manager/worker model is shown below.

code for manager              code for worker

for i from 1 to p-1 do
    receive from i            send to manager
for i from 1 to p-1 do
    send to i                 receive from manager

The counter implementation of a barrier or linear barrier is effective but it takes \(O(p)\) steps. A schematic of the steps to synchronize 8 processes is shown in Fig. 48 for a linear and a tree barrier.

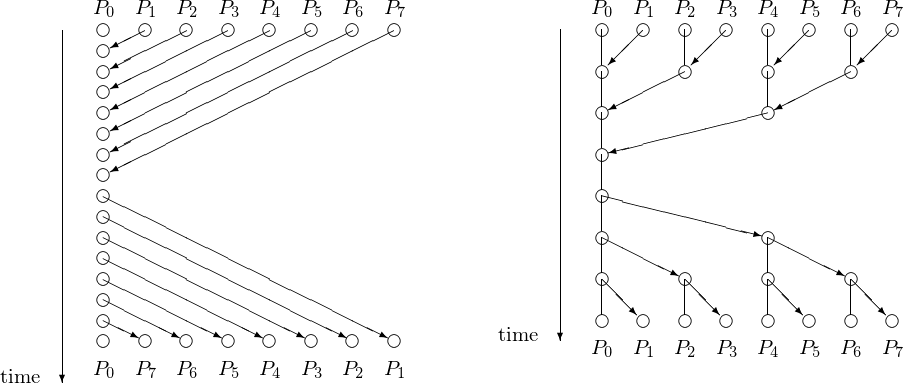
Fig. 48 A linear next to a tree barrier to synchronize 8 processes. For 8 processes, the linear barrier takes twice as many time steps as the tree barrier.

Implementing a tree barrier we write pseudo code for the trapping and the release phase, for \(p = 2^k\) (recall the fan in gather and the fan out scatter):

The trapping phase is defined below:

for i from k-1 down to 0 do
    for j from 2**i to 2**(i+1) do
        node j sends to node j - 2**i
        node j - 2**i receives from node j.

The release phase is defined below

for i from 0 to k-1 do
    for j from 0 to 2**i-1  do
        node j sends to j + 2**i
        node j + 2**i receives from node j.

Observe that two processes can synchronize in one step. We can generalize this into a tree barrier so there are no idle processes. This leads to a butterfly barrier shown in Fig. 49.

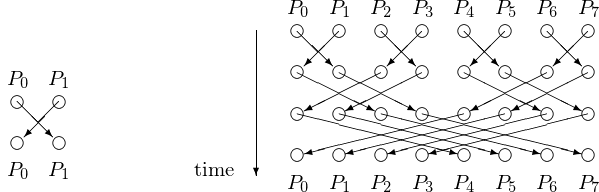
Fig. 49 Two processes can synchronize in one step as shown on the left. At the right is a schematic of the time steps for a tree barrier to synchronize 8 processes.

The algorithm for a butterfly barrier, for \(p = 2^k\), is described is pseudo code below.

for i from 0 to k-1 do
    s := 0
    for j from 0 to p-1 do
        if (j mod 2**(i+1) = 0) s := j
        node j sends to node ((j + 2**i) mod 2**(i+1)) + s
        node ((j + 2**i) mod 2^(i+1)) + s receives from node j

To avoid deadlock, ensuring that every send is matched with a corresponding receive, we can work with a sendrecv, as shown in Fig. 50.

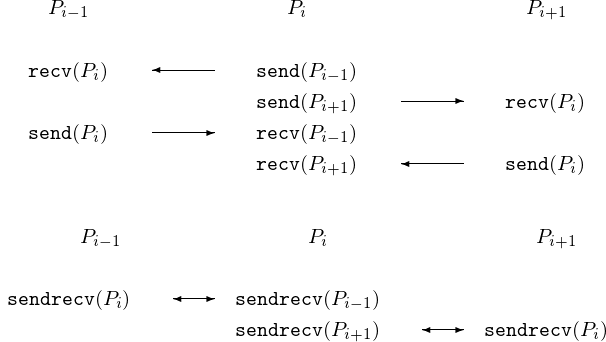
Fig. 50 The top picture is equivalent to the bottom picture.

The sendrecv in MPI has the following form:

MPI_Sendrecv(sendbuf,sendcount,sendtype,dest,sendtag,
             recvbuf,recvcount,recvtype,source,recvtag,comm,status)

where the parameters are in Table 17.

Table 17 Parameters of sendrecv in MPI.¶
parameter	description
sendbuf	initial address of send buffer
sendcount	number of elements in send buffer
sendtype	type of elements in send buffer
dest	rank of destination
sendtag	send tag
recvbuf	initial address of receive buffer
recvcount	number of elements in receive buffer
sendtype	type of elements in receive buffer
source	rank of source or MPI_ANY_SOURCE
recvtag	receive tag or MPI_ANY_TAG
comm	communicator
status	status object

We illustrate MPI_Sendrecv to synchronize two nodes. Processors 0 and 1 swap characters in a bidirectional data transfer.

$ mpirun -np 2 /tmp/use_sendrecv
Node 0 will send a to 1
Node 0 received b from 1
Node 1 will send b to 0
Node 1 received a from 0
$

with code below:

#include <stdio.h>
#include <mpi.h>

#define sendtag 100

int main ( int argc, char *argv[] )
{
   int i,j;
   MPI_Status status;

   MPI_Init(&argc,&argv);
   MPI_Comm_rank(MPI_COMM_WORLD,&i);

   char c = 'a' + (char)i; /* send buffer */
   printf("Node %d will send %c to %d\n",i,c,j);
   char d;                 /* receive buffer */

   MPI_Sendrecv(&c,1,MPI_CHAR,j,sendtag,&d,1,MPI_CHAR,MPI_ANY_SOURCE,
                MPI_ANY_TAG,MPI_COMM_WORLD,&status);

   printf("Node %d received %c from %d\n",i,d,j);
}

MPI_Finalize();
return 0;

The Prefix Sum Algorithm¶

A data parallel computation is a computation where the same operations are preformed on different data simultaneously. The benefits of data parallel computations is that they are easy to program, scale well, and are fit for SIMD computers. The problem we consider is to compute \(\displaystyle \sum_{i=0}^{n-1} a_i\) for \(n = p = 2^k\). This problem is related to the composite trapezoidal rule.

For \(n = 8\) and \(p = 8\), the prefix sum algorithm is illustrated in Fig. 51.

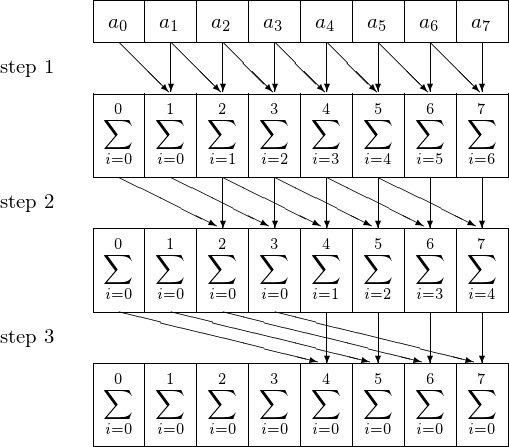
Fig. 51 The prefix sum for \(n = 8 = p\).

Pseudo code for the prefix sum algorithm for \(n = p = 2^k\) is below. Processor i executes:

s := 1
x := a[i]
for j from 0 to k-1 do
    if (j < p - s + 1) send x to processor i+s
    if (j > s-1) receive y from processor i-s
                 add y to x: x := x + y
    s := 2*s

The speedup: \(\displaystyle \frac{p}{\log_2(p)}\). Communication overhead: one send/recv in every step.

The prefix sum algorithm can be coded up in MPI as in the program below.

#include <stdio.h>
#include "mpi.h"
#define tag 100               /* tag for send/recv */

int main ( int argc, char *argv[] )
{
   int i,j,nb,b,s;
   MPI_Status status;
   const int p = 8;        /* run for 8 processors */

   MPI_Init(&argc,&argv);
   MPI_Comm_rank(MPI_COMM_WORLD,&i);

   nb = i+1;            /* node i holds number i+1 */
   s = 1;     /* shift s will double in every step */

   for(j=0; j<3; j++)              /* 3 stages, as log2(8) = 3 */
   {
      if(i < p - s)     /* every one sends, except last s ones */
         MPI_Send(&nb,1,MPI_INT,i+s,tag,MPI_COMM_WORLD);
      if(i >= s)     /* every one receives, except first s ones */
      {
         MPI_Recv(&b,1,MPI_INT,i-s,tag,MPI_COMM_WORLD,&status);
         nb += b;       /* add received value to current number */
      }
      MPI_Barrier(MPI_COMM_WORLD);  /* synchronize computations */
      if(i < s)
         printf("At step %d, node %d has number %d.\n",j+1,i,nb);
      else
         printf("At step %d, Node %d has number %d = %d + %d.\n",
                j+1,i,nb,nb-b,b);
   s *= 2;                               /* double the shift */
   }
   if(i == p-1) printf("The total sum is %d.\n",nb);

   MPI_Finalize();
   return 0;
}

Running the code prints the following to screen:

$ mpirun -np 8 /tmp/prefix_sum
At step 1, node 0 has number 1.
At step 1, Node 1 has number 3 = 2 + 1.
At step 1, Node 2 has number 5 = 3 + 2.
At step 1, Node 3 has number 7 = 4 + 3.
At step 1, Node 7 has number 15 = 8 + 7.
At step 1, Node 4 has number 9 = 5 + 4.
At step 1, Node 5 has number 11 = 6 + 5.
At step 1, Node 6 has number 13 = 7 + 6.
At step 2, node 0 has number 1.
At step 2, node 1 has number 3.
At step 2, Node 2 has number 6 = 5 + 1.
At step 2, Node 3 has number 10 = 7 + 3.
At step 2, Node 4 has number 14 = 9 + 5.
At step 2, Node 5 has number 18 = 11 + 7.
At step 2, Node 6 has number 22 = 13 + 9.
At step 2, Node 7 has number 26 = 15 + 11.
At step 3, node 0 has number 1.
At step 3, node 1 has number 3.
At step 3, node 2 has number 6.
At step 3, node 3 has number 10.
At step 3, Node 4 has number 15 = 14 + 1.
At step 3, Node 5 has number 21 = 18 + 3.
At step 3, Node 6 has number 28 = 22 + 6.
At step 3, Node 7 has number 36 = 26 + 10.
The total sum is 36.

Barriers in Shared Memory Parallel Programming¶

Recall Pthreads and the work crew model. Often all threads must wait till on each other. We will illustrate the pthread_barrier_t with a small illustrative example.

int count = 3;
pthread_barrier_t our_barrier;
p_thread_barrier_init(&our_barrier, NULL, count);

In the example above, we initialized the barrier that will cause as many threads as the value of count to wait. A thread remains trapped waiting as long as fewer than count many threads have reached pthread_barrier_wait(&our_barrier); and the pthread_barrier_destroy(&our_barrier) should only be executed after all threads have finished.

In our illustrative program, each thread generates a random number, rolling a 6-sided die and then sleeps as many seconds as the value of the die (which is an integer number ranging from 1 till 6). The sleeping times are recorded in a shared array that is declared as a global variable. So the shared data is the time each thread sleeps. Each threads prints only after each thread has written its sleeping time in the shared data array. A screen shot of the program running with 5 threads is below.

$ /tmp/pthread_barrier_example
Give the number of threads : 5
Created 5 threads ...
Thread 0 has slept 2 seconds ...
Thread 2 has slept 2 seconds ...
Thread 1 has slept 4 seconds ...
Thread 3 has slept 5 seconds ...
Thread 4 has slept 6 seconds ...
Thread 4 has data : 24256
Thread 3 has data : 24256
Thread 2 has data : 24256
Thread 1 has data : 24256
Thread 0 has data : 24256
$

The code should be compiled with the -lpthread option, if for example, the file pthread_barrier_example.c contains the C code, then the compilation command could be

$ gcc -lpthread pthread_barrier_example.c -o /tmp/pthread_barrier_example

The global variables size, data, and our_barrier will be initialized in the main program. The user is prompted to enter size, the number of threads. The array data is allocated with size elements; The barrier our_barrier is initialized. Code for the complete program is below:

#include <stdlib.h>
#include <stdio.h>
#include <pthread.h>

int size;   /* size equals the number of threads */
int *data;  /* shared data, as many ints as size */
pthread_barrier_t our_barrier; /* to synchronize */

void *fun ( void *args )
{
   int *id = (int*) args;
   int r = 1 + (rand() % 6);
   int k;
   char strd[size+1];

   sleep(r);
   printf("Thread %d has slept %d seconds ...\n", *id, r);
   data[*id] = r;

   pthread_barrier_wait(&our_barrier);

   for(k=0; k<size; k++) strd[k] = '0' + ((char) data[k]);
   strd[size] = '\0';

   printf("Thread %d has data : %s\n", *id, strd);
}

int main ( int argc, char* argv[] )
{
   printf("Give the number of threads : "); scanf("%d", &size);
   data = (int*) calloc(size, sizeof(int));
   {
      pthread_t t[size];
      pthread_attr_t a;
      int id[size], i;

      pthread_barrier_init(&our_barrier, NULL, size);

      for(i=0; i<size; i++)
      {
         id[i] = i;
         pthread_attr_init(&a);
         if(pthread_create(&t[i], &a, fun, (void*)&id[i]) != 0)
            printf("Unable to create thread %d!\n", i);
      }
      printf("Created %d threads ...\n", size);
      for(i=0; i<size; i++) pthread_join(t[i], NULL);

      pthread_barrier_destroy(&our_barrier);
   }
   return 0;
}

Bibliography¶

W. Daniel Hillis and Guy L. Steele. Data Parallel Algorithms. Communications of the ACM, vol. 29, no. 12, pages 1170-1183, 1986.
B. Wilkinson and M. Allen. Parallel Programming. Techniques and Applications Using Networked Workstations and Parallel Computers. Prentice Hall, 2nd edition, 2005.

Exercises¶

Write code using MPI_sendrecv for a butterfly barrier. Show that your code works for \(p = 8\).
Rewrite prefix_sum.c using MPI_sendrecv.
Consider the composite trapezoidal rule for the approximation of \(\pi\) (see lecture 13), doubling the number of intervals in each step. Can you apply the prefix sum algorithm so that at the end, processor \(i\) holds the approximation for \(\pi\) with \(2^i\) intervals?

Barriers for Synchronizations¶

Synchronizing Computations¶

The Prefix Sum Algorithm¶

Barriers in Shared Memory Parallel Programming¶

Bibliography¶

Exercises¶

Table Of Contents

Previous topic

Next topic

This Page