Introduction to CUDA¶
Our first GPU Program¶
We will run Newton’s method in complex arithmetic as our first CUDA program.
To compute \(\sqrt{c}\) for \(c \in {\mathbb cc}\), we apply Newton’s method on \(x^2 - c = 0\):
Five iterations suffice to obtain an accurate value for \(\sqrt{c}\).
Finding roots is relevant for scientific computing. But, is this computation suitable for the GPU? The data parallelism we can find in this application is that we can run Newton’s method for many different \(c\)‘s. With a little more effort, the code in this section can be extended to a complex root finder for polynomials in one variable.
To examine the CUDA Compute Capability,
we check the card with deviceQuery.
$ /usr/local/cuda/samples/1_Utilities/deviceQuery/deviceQuery
/usr/local/cuda/samples/1_Utilities/deviceQuery/deviceQuery Starting...
CUDA Device Query (Runtime API) version (CUDART static linking)
Detected 3 CUDA Capable device(s)
Device 0: "Tesla K20c"
CUDA Driver Version / Runtime Version 6.0 / 5.5
CUDA Capability Major/Minor version number: 3.5
Total amount of global memory: 4800 MBytes (5032706048 bytes)
(13) Multiprocessors, (192) CUDA Cores/MP: 2496 CUDA Cores
GPU Clock rate: 706 MHz (0.71 GHz)
Memory Clock rate: 2600 Mhz
Memory Bus Width: 320-bit
L2 Cache Size: 1310720 bytes
Maximum Texture Dimension Size (x,y,z) 1D=(65536), 2D=(65536, 65536), 3D=(4096, 4096, 4096)
Maximum Layered 1D Texture Size, (num) layers 1D=(16384), 2048 layers
Maximum Layered 2D Texture Size, (num) layers 2D=(16384, 16384), 2048 layers
Total amount of constant memory: 65536 bytes
Total amount of shared memory per block: 49152 bytes
Total number of registers available per block: 65536
Warp size: 32
Maximum number of threads per multiprocessor: 2048
Maximum number of threads per block: 1024
Max dimension size of a thread block (x,y,z): (1024, 1024, 64)
Max dimension size of a grid size (x,y,z): (2147483647, 65535, 65535)
Maximum memory pitch: 2147483647 bytes
Texture alignment: 512 bytes
Concurrent copy and kernel execution: Yes with 2 copy engine(s)
Run time limit on kernels: No
Integrated GPU sharing Host Memory: No
Support host page-locked memory mapping: Yes
Alignment requirement for Surfaces: Yes
Device has ECC support: Enabled
Device supports Unified Addressing (UVA): Yes
Device PCI Bus ID / PCI location ID: 4 / 0
Compute Mode:
< Default (multiple host threads can use ::cudaSetDevice() with device simultaneously) >
Another standard check is the bandwidthTest,
which runs as below.
$ /usr/local/cuda/samples/1_Utilities/bandwidthTest/bandwidthTest
[CUDA Bandwidth Test] - Starting...
Running on...
Device 0: Tesla K20c
Quick Mode
Host to Device Bandwidth, 1 Device(s)
PINNED Memory Transfers
Transfer Size (Bytes) Bandwidth(MB/s)
33554432 5819.5
Device to Host Bandwidth, 1 Device(s)
PINNED Memory Transfers
Transfer Size (Bytes) Bandwidth(MB/s)
33554432 6415.8
Device to Device Bandwidth, 1 Device(s)
PINNED Memory Transfers
Transfer Size (Bytes) Bandwidth(MB/s)
33554432 143248.0
Result = PASS
CUDA Program Structure¶
There are five steps to get GPU code running:
- C and C++ functions are labeled with CUDA keywords
__device__,__global__, or__host__. - Determine the data for each thread to work on.
- Transferring data from/to host (CPU) to/from the device (GPU).
- Statements to launch data-parallel functions, called kernels.
- Compilation with
nvcc.
We will now examine every step in greater detail.
In the first step, we add CUDA extensions to functions. We distinguish between three keywords before a function declaration:
__host__: The function will run on the host (CPU).__device__: The function will run on the device (GPU).__global__: The function is called from the host but runs on the device. This function is called a kernel.
The CUDA extensions to C function declarations are summarized in Table 26.
| executed on | callable from | |
|---|---|---|
__device__ double D() |
device | device |
__global__ void K() |
device | host |
__host__ int H() |
host | host |
In the second step, we determine the data for each thread. The grid consists of N blocks, with \({\tt blockIdx.x} \in \{0,N-1\}\). Within each block, \({\tt threadIdx.x} \in \{ 0, {\tt blockDim.x}-1\}\). This second step is illustrated in Fig. 86.
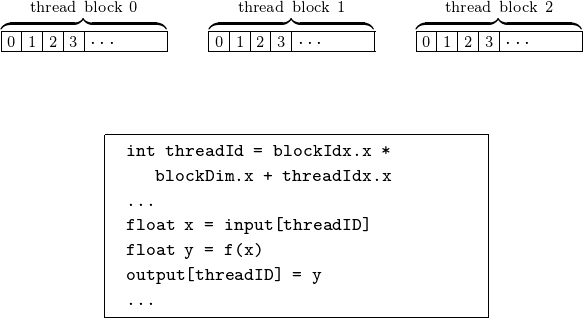
Fig. 86 Defining the data for each thread.
In the third step, data is allocated and transferred from the host to the device. We illustrate this step with the code below.
cudaDoubleComplex *xhost = new cudaDoubleComplex[n];
// we copy n complex numbers to the device
size_t s = n*sizeof(cudaDoubleComplex);
cudaDoubleComplex *xdevice;
cudaMalloc((void**)&xdevice,s);
cudaMemcpy(xdevice,xhost,s,cudaMemcpyHostToDevice);
// allocate memory for the result
cudaDoubleComplex *ydevice;
cudaMalloc((void**)&ydevice,s);
// copy results from device to host
cudaDoubleComplex *yhost = new cudaDoubleComplex[n];
cudaMemcpy(yhost,ydevice,s,cudaMemcpyDeviceToHost);
In the fourth step, the kernel is launched. The kernel is declared as
__global__ void squareRoot
( int n, cudaDoubleComplex *x, cudaDoubleComplex *y )
// Applies Newton's method to compute the square root
// of the n numbers in x and places the results in y.
{
int i = blockIdx.x*blockDim.x + threadIdx.x;
...
For frequency f, dimension n,
and block size w, we do:
// invoke the kernel with n/w blocks per grid
// and w threads per block
for(int i=0; i<f; i++)
squareRoot<<<n/w,w>>>(n,xdevice,ydevice);
In the fifth step, the code is compiled with nvcc.
Then, if the makefile contains
runCudaComplexSqrt:
nvcc -o /tmp/run_cmpsqrt -arch=sm_13 \
runCudaComplexSqrt.cu
typing make runCudaComplexSqrt does
nvcc -o /tmp/run_cmpsqrt -arch=sm_13 runCudaComplexSqrt.cu
The -arch=sm_13 is needed for double arithmetic.
The code to compute complex roots is below. Complex numbers and their arithmetic is defined on the host and on the device.
#ifndef __CUDADOUBLECOMPLEX_CU__
#define __CUDADOUBLECOMPLEX_CU__
#include <cmath>
#include <cstdlib>
#include <iomanip>
#include <vector_types.h>
#include <math_functions.h>
typedef double2 cudaDoubleComplex;
We use the double2 of vector_types.h to define
complex numbers because double2 is a native CUDA type
allowing for coalesced memory access.
Random complex numbers are generated with the function below.
__host__ cudaDoubleComplex randomDoubleComplex()
// Returns a complex number on the unit circle
// with angle uniformly generated in [0,2*pi].
{
cudaDoubleComplex result;
int r = rand();
double u = double(r)/RAND_MAX;
double angle = 2.0*M_PI*u;
result.x = cos(angle);
result.y = sin(angle);
return result;
}
Calling sqrt of math_functions.h is done in the function below.
__device__ double radius ( const cudaDoubleComplex c )
// Returns the radius of the complex number.
{
double result;
result = c.x*c.x + c.y*c.y;
return sqrt(result);
}
We overload the output operator.
__host__ std::ostream& operator<<
( std::ostream& os, const cudaDoubleComplex& c)
// Writes real and imaginary parts of c,
// in scientific notation with precision 16.
{
os << std::scientific << std::setprecision(16)
<< c.x << " " << c.y;
return os;
}
Complex addition is defined with operator overloading, as in the function below.
__device__ cudaDoubleComplex operator+
( const cudaDoubleComplex a, const cudaDoubleComplex b )
// Returns the sum of a and b.
{
cudaDoubleComplex result;
result.x = a.x + b.x;
result.y = a.y + b.y;
return result;
}
The rest of the arithmetical operations are defined
in a similar manner.
All definitions related to complex numbers are stored
in the file cudaDoubleComplex.cu.
The kernel function to compute the square root is listed below.
#include "cudaDoubleComplex.cu"
__global__ void squareRoot
( int n, cudaDoubleComplex *x, cudaDoubleComplex *y )
// Applies Newton's method to compute the square root
// of the n numbers in x and places the results in y.
{
int i = blockIdx.x*blockDim.x + threadIdx.x;
cudaDoubleComplex inc;
cudaDoubleComplex c = x[i];
cudaDoubleComplex r = c;
for(int j=0; j<5; j++)
{
inc = r + r;
inc = (r*r - c)/inc;
r = r - inc;
}
y[i] = r;
}
The main function takes command line arguments as defined below.
int main ( int argc, char*argv[] )
{
if(argc < 5)
{
cout << "call with 4 arguments : " << endl;
cout << "dimension, block size, frequency, and check (0 or 1)"
<< endl;
}
else
{
int n = atoi(argv[1]); // dimension
int w = atoi(argv[2]); // block size
int f = atoi(argv[3]); // frequency
int t = atoi(argv[4]); // test or not
The main program generates n random complex numbers
with radius one. After the generation of the data,
the data is transferred and the kernel is launched.
// we generate n random complex numbers on the host
cudaDoubleComplex *xhost = new cudaDoubleComplex[n];
for(int i=0; i<n; i++) xhost[i] = randomDoubleComplex();
// copy the n random complex numbers to the device
size_t s = n*sizeof(cudaDoubleComplex);
cudaDoubleComplex *xdevice;
cudaMalloc((void**)&xdevice,s);
cudaMemcpy(xdevice,xhost,s,cudaMemcpyHostToDevice);
// allocate memory for the result
cudaDoubleComplex *ydevice;
cudaMalloc((void**)&ydevice,s);
// invoke the kernel with n/w blocks per grid
// and w threads per block
for(int i=0; i<f; i++)
squareRoot<<<n/w,w>>>(n,xdevice,ydevice);
// copy results from device to host
cudaDoubleComplex *yhost = new cudaDoubleComplex[n];
cudaMemcpy(yhost,ydevice,s,cudaMemcpyDeviceToHost);
To verify the correctness, there is the option to test one random number.
if(t == 1) // test the result
{
int k = rand() % n;
cout << "testing number " << k << endl;
cout << " x = " << xhost[k] << endl;
cout << " sqrt(x) = " << yhost[k] << endl;
cudaDoubleComplex z = Square(yhost[k]);
cout << "sqrt(x)^2 = " << z << endl;
}
}
return 0;
}
The scalable programming model of the GPU is illustrated in Fig. 87.
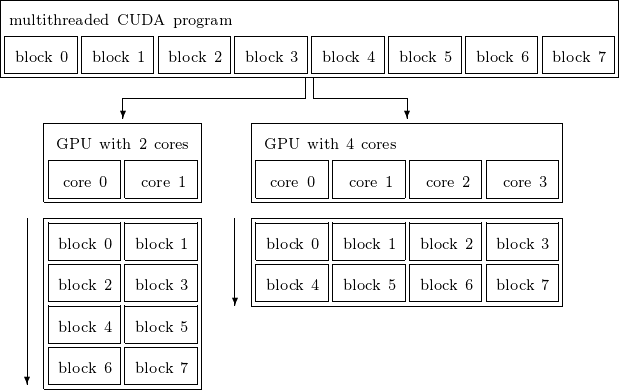
Fig. 87 A scalable programming model.
To run the code, we first test the correctness.
$ /tmp/run_cmpsqrt 1 1 1 1
testing number 0
x = 5.3682227446949737e-01 -8.4369535119816541e-01
sqrt(x) = 8.7659063264145631e-01 -4.8123680528950746e-01
sqrt(x)^2 = 5.3682227446949726e-01 -8.4369535119816530e-01
On 64,000 numbers, 32 threads in a block, doing it 10,000 times:
$ time /tmp/run_cmpsqrt 64000 32 10000 1
testing number 50325
x = 7.9510606509728776e-01 -6.0647039931517477e-01
sqrt(x) = 9.4739275517002119e-01 -3.2007337822967424e-01
sqrt(x)^2 = 7.9510606509728765e-01 -6.0647039931517477e-01
real 0m1.618s
user 0m0.526s
sys 0m0.841s
Then we change the number of thread in a block.
$ time /tmp/run_cmpsqrt 128000 32 100000 0
real 0m17.345s
user 0m9.829s
sys 0m7.303s
$ time /tmp/run_cmpsqrt 128000 64 100000 0
real 0m10.502s
user 0m5.711s
sys 0m4.497s
$ time /tmp/run_cmpsqrt 128000 128 100000 0
real 0m9.295s
user 0m5.231s
sys 0m3.865s
In five steps we wrote our first complete CUDA program.
We started chapter 3 of the textbook by Kirk & Hwu,
covering more of the CUDA Programming Guide.
Available in /usr/local/cuda/doc
and at <http://www.nvidia.com> are
the CUDA C Best Practices Guide
and the CUDA Programming Guide.
Many examples of CUDA applications are available in
/usr/local/cuda/samples.
Exercises¶
- Instead of 5 Newton iterations in
runCudaComplexSqrt.cuusekiterations wherekis entered by the user at the command line. What is the influence ofkon the timings? - Modify the kernel for the complex square root so it takes on input an array of complex coefficients of a polynomial of degree \(d\). Then the root finder applies Newton’s method, starting at random points. Test the correctness and experiment to find the rate of success, i.e.: for polynomials of degree \(d\) how many random trials are needed to obtain \(d/2\) roots of the polynomial?