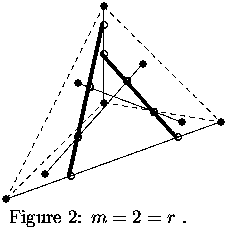Next: The Principles of Polynomial
Up: Polynomial Homotopies for dense,
Previous: Introduction
The classification in Table 1 is inspired by [44].
The dense class is closest to the common algebraic description, whereas
the determinantal systems arise in enumerative geometry.
Table 1:
Key words of the three classes of polynomial systems.
| system |
model |
theory |
space |
| dense |
highest degrees |
Bézout |
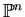 |
projective |
| sparse |
Newton polytopes |
Bernshtein |
 |
toric |
| determinantal |
localization posets |
Schubert |
Gmr |
Grassmannian |
|
For the vector of unknowns
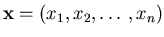 and exponents
and exponents
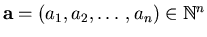 ,
denote
,
denote
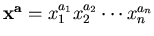 .
A polynomial system
.
A polynomial system
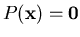 is given by
is given by
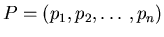 ,
a tuple of polynomials
,
a tuple of polynomials
![$p_i \in {\Bbb C}[{\bf x}]$](img17.gif) ,
,
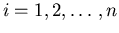 .
.
The complexity of a dense polynomial p is
measured by its degree d:
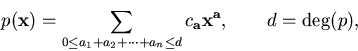 |
(1) |
where at least one monomial of degree d should have a nonzero coefficient.
The total degree D of a dense system P is
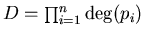 .
.
Theorem 2.1 (Bézout [
15])
The system
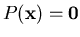
has
no more than
D isolated solutions, counted with multiplicities.
Consider for example
 |
(2) |
Although D = 16, this system has only eight solutions because of its
sparse structure.
The support A of a sparse polynomial p collects all
exponents of those monomials whose coefficients are nonzero.
Since we allow negative exponents (
 ),
we restrict
),
we restrict
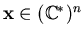 ,
,
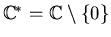 .
.
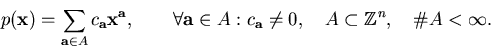 |
(3) |
The Newton polytope Q of p is the convex hull of the support Aof p.
We model the structure of a sparse system P by a tuple of Newton
polytopes
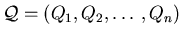 ,
spanned by
,
spanned by
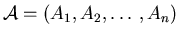 ,
the so-called supports of P.
,
the so-called supports of P.
The volume of a positive linear combination of polytopes is a homogeneous
polynomial in the multiplication factors.
The coefficients are mixed volumes.
For instance, for (Q1,Q2), we write:
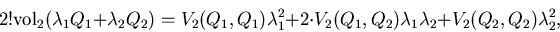 |
(4) |
normalizing
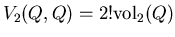 .
For the Newton polytopes of the system (2):
.
For the Newton polytopes of the system (2):
 .
To interpret this we look at Figure 1 and see that multiplying
P1 and P2 respectively by
.
To interpret this we look at Figure 1 and see that multiplying
P1 and P2 respectively by 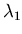 and
and 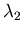 changes their
areas respectively with
changes their
areas respectively with
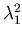 and
and
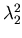 .
The cells in the subdivision of Q1 + Q2 whose area is scaled by
.
The cells in the subdivision of Q1 + Q2 whose area is scaled by
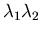 contribute to the mixed volume.
So, for the example in (2), the root count is eight.
contribute to the mixed volume.
So, for the example in (2), the root count is eight.
Figure 1:
Newton polytopes Q1, Q2, a mixed subdivision
of Q1 + Q2 with volumes.
 |
Theorem 2.2 (Bernshtein [
7])
A system
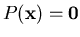
with Newton polytopes
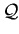
has no
more than
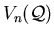
isolated solutions in
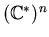
,
counted with multiplicities.
The mixed volume was nicknamed [13] as the BKK bound to honor
Bernshtein [7], Kushnirenko [51], and
Khovanskii [49].
For the third class of polynomial systems we consider a matrix [C | X]where
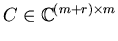 and
and
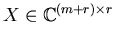 respectively collect the coefficients and indeterminates.
Laplace expansion of the maximal minors of [C | X] in m-by-m and
r-by-r minors yields a determinantal polynomial
respectively collect the coefficients and indeterminates.
Laplace expansion of the maximal minors of [C | X] in m-by-m and
r-by-r minors yields a determinantal polynomial
![\begin{displaymath}
p({\bf x}) = \sum_{\scriptsize\begin{array}{c} I \cup J = U...
...} } {\rm sign}(I,J) C[I] X[J],
\quad U = \{ 1,2,\ldots,m+r\},
\end{displaymath}](img41.gif) |
(5) |
where the summation runs over all distinct choices I of m elements of U.
The partition
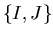 of U defines the permutation
of U defines the permutation
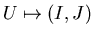 with
with
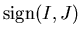 its sign.
The symbols C[I] and X[I] respectively represent
coefficient minors and minors of indeterminates.
Note that for more general intersection conditions, the matrices
[C | X] are not necessarily square.
its sign.
The symbols C[I] and X[I] respectively represent
coefficient minors and minors of indeterminates.
Note that for more general intersection conditions, the matrices
[C | X] are not necessarily square.
The vanishing of a polynomial as in (5) expresses
the condition that the r-plane X meets a given m-plane nontrivially.
The counting and finding of all figures that satisfy certain geometric
conditions is the central theme of enumerative geometry.
For example, consider the following.
Theorem 2.3 (Schubert [
91])
Let
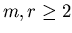
.
In
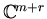
there are
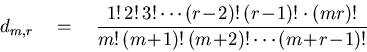 |
(6) |
r-planes that nontrivially meet
mr given
m-planes in general position.
This root count dm,r is sharp compared to other root counts,
see [98] and [114] for examples.
We can picture the simplest case, using the fact that 2-planes in
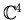 represent lines in
represent lines in
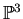 .
In Figure 2 the positive real projective 3-space
corresponds to the interior of the tetrahedron.
.
In Figure 2 the positive real projective 3-space
corresponds to the interior of the tetrahedron.
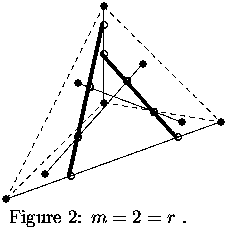

Algorithmic proofs for the above theorems consist in two steps.
First we show how to construct a generic start system that has exactly
as many regular solutions as the root count.
Then we set up a homotopy for which all isolated solutions of any
particular target system lie at the end of some solution path
originating at some solution of the constructed start system.




Next: The Principles of Polynomial
Up: Polynomial Homotopies for dense,
Previous: Introduction
Jan Verschelde
2001-04-08
![]() and exponents
and exponents
![]() ,
denote
,
denote
![]() .
A polynomial system
.
A polynomial system
![]() is given by
is given by
![]() ,
a tuple of polynomials
,
a tuple of polynomials
![]() ,
,
![]() .
.
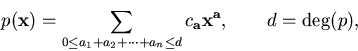
![]() ),
we restrict
),
we restrict
![]() ,
,
![]() .
.
![]() and
and
![]() respectively collect the coefficients and indeterminates.
Laplace expansion of the maximal minors of [C | X] in m-by-m and
r-by-r minors yields a determinantal polynomial
respectively collect the coefficients and indeterminates.
Laplace expansion of the maximal minors of [C | X] in m-by-m and
r-by-r minors yields a determinantal polynomial
![]() represent lines in
represent lines in
![]() .
In Figure 2 the positive real projective 3-space
corresponds to the interior of the tetrahedron.
.
In Figure 2 the positive real projective 3-space
corresponds to the interior of the tetrahedron.