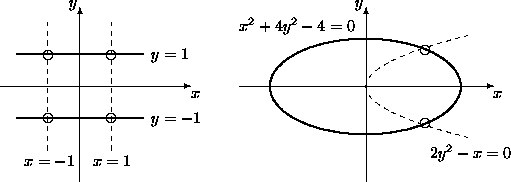The Geometry of the Deformations

Homotopy methods have an intuitive geometric interpretation. In this section we illustrate the geometry of the three types of moving into special position: product, toric, and Pieri deformations. These can be regarded as three applications of the principle of continuity or conservation of number in enumerative geometry.

Product homotopies deform polynomial equations into products of linear equations. In Figure 4 we see the line configuration at the start and the ellipse-parabola intersection in the end. Note that complex space is the natural space for deformations. The other two complex conjugated intersection points could not be displayed in Figure 4.

  

Figure 4: Intersection of quadrics: a degenerate and a target configuration.

The sparser a system, the easier it can be solved. In Figure 5 we illustrate the idea of making a system sparser by setting up a so-called polyhedral homotopy that reduces this particular system at t=0 to a linear system. The lower hull of the Newton polytope of this homotopy induces a triangulation, which is used to count the roots. In particular, every cell in the triangulation gives rise to a homotopy with as many paths to follow as the volume of the cell. The other root for the example in Figure 5 can be computed with a homotopy obtained from  $\widehat P$ by the substitution of variables $x_1 \leftarrow {\widetilde x}_1 t^{-1}$ and $x_2 \leftarrow {\widetilde x}_2 t^{-1}$. This transformation pushes the constant monomial up, so that at t=0 we have the nonconstant monomials in the start system to compute the other root.

  

Figure: Triangulation of the Newton polytope of P with polyhedral homotopy $\widehat P$.

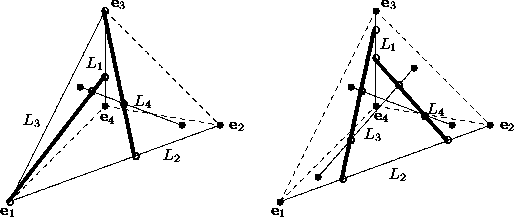
Figure 6 displays a special and a general configuration of four lines. The basis has been chosen such that two of the four input lines are spanned by standard basis vectors. To compute all lines that meet four given lines, one of the four given lines is moved into special position so that it intersects two other given lines, see the left of Figure 6. The solution lines must then originate at those two intersection points and reach to the other opposite line while meeting the line left in general position.

  

Figure: In ${\Bbb P}^3$ two thick lines meet four given lines L₁, L₂, L₃, and L₄ in a point. At the left we see a special configuration and the general configuration is at the right.

The constructions above are in a sense [1] ``heuristic proofs''. With the general position assumption we cheat a bit, avoiding the hard problem of assigning multiplicities. Making this so-called [127] ``method of degeneration'' rigorous was an important development in algebraic geometry.

To deal with solution paths diverging to ill-conditioned roots or to infinity we need to compactify our space. Instead of polynomials in n variables we consider homogeneous forms with coordinates subject to equivalence relations. While mathematically all coordinate choices are equivalent, we select the numerically most favorable representations of the solutions.

The usual projective transformation consists in the change of variables $x_i := \frac{z_i}{z_0}$, for $i = 1,2,\ldots,n$, which leads to the homogeneous system $P({\bf z}) = {\bf0}$. To have as many equations as unknowns, we add to this system a random hyperplane. Except for an algebraic set of the coefficients of this added hyperplane, all solution paths are guaranteed to stay inside ${\Bbb C}^{n+1}$ when homotopy continuation is applied. We refer to [64] for numerical techniques that dynamically restrict the computations to n dimensions.

For sparse polynomial systems, we introduce as in [116] a new variable for every facet of the Newton polytopes. The advantage of this more involved compactification is based on the observation that when paths diverge to infinity certain coefficients of the polynomial system become dominant. With toric homogenization the added variables that become zero identify the faces of the Newton polytopes for the parts of the system that become dominant. This compactification works in conjunction with polyhedral end games [43] which are summarized in Section 5.3.

The natural way to compactify G_mr is to consider a multi-projective homogenization according to rows or columns of the matrix representations for the planes. In addition, we have that the planes are equivalent upon a linear change of basis. Choosing orthonormal matrices to represent the input planes leads to drastic improvements in the conditioning of the solution paths, see [46] and [114] for experimental data.