by Louis H. Kauffman
The trefoil knot is the simplest knot. However, it also has some very interesting geometric forms. For example, in these web pages you will find a description of Fourier knots and the simplest representation of the trefoil in a harmonic parametrization. You can go directly to that part of the site via: Fourier Trefoil and The Pattern
In that part of the site you will also find a discussion and reference to the so-called "Pattern Knot" seen by Lynnclaire Dennis. Her Pattern Knot is rounder than the Fourier version, and actually somewhat more like the DoubleHelix version of the trefoil that you will see in this part of the site.
The knot you are about to see is formed by taking two helices, each of one and one-half turns and plugging them into one another at a ninety degree angle.
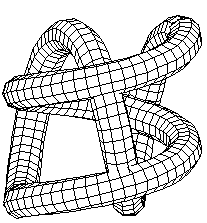
Here is another view of the DoubleHelix Trefoil.
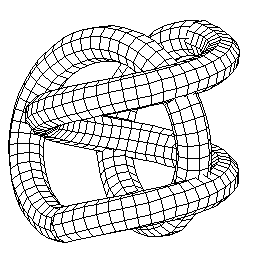
Here are two helices meeting at ninety degrees to produce the DoubleHelix Trefoil where they meet.

Finally, here are a few more shots of that knot.
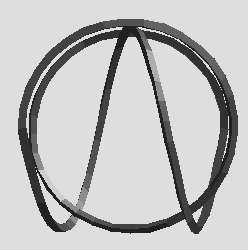
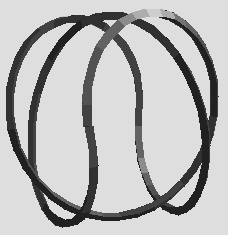

Perhaps you are wondering what the equation is for these knots. Well here it is.
First helix:
Second helix:
SAM = Science + Art + Mathematics.