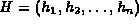Polynomial Homotopy Continuation Methods

The name Polynomial Homotopy Continuation unites the three key concepts of the method. Because we solve polynomial systems we exploit the algebraic structure to count the number of roots and to construct a start system. By continuation methods the known solutions of the start system are extended to the desired solutions of the target system. This deformation is defined by the homotopy, that is a family of systems connecting start and target system.

Nowadays we can distinguish three different types of homotopies 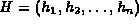, that can be applied each at a different stage of the solver.

1. Solving a generic system by polyhedral homotopy continuation.

   A polyhedral homotopy is induced by a lifting function 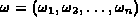on the supports 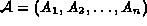of the polynomial system.

   

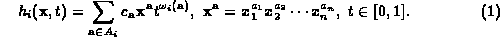
   Polyhedral homotopies lead to an optimal number of solution paths, provided the coefficients are sufficiently chosen at random.

2. A convex-linear homotopy for solving one target system.

   The following artificial-parameter homotopy is commonly used:

   

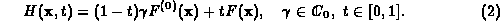
   The system 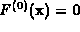is the start system of the homotopy. A good homotopy should lead to smooth solution paths which allow to reach all isolated solutions at t=1.

3. Coefficient-parameter polynomial continuation.

   This type of homotopy is a natural-parameter homotopy where the coefficients are viewed as functions of the continuation parameter t.

   

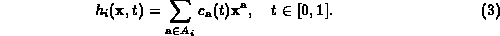
   This type of homotopy allows to study numerically the solution sets in terms of the significant parameters of the polynomial system.

We illustrate how to compute the intersection of an ellipse and a parabola by means of a homotopy continuation method. The root count equals four. On the left of Figure 1 is a degenerate configuration as start system to compute the common intersection points.

  
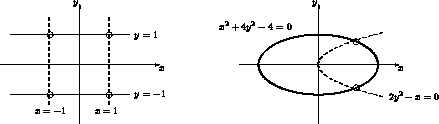
Figure 1: Intersection of quadratics: a degenerate and a target configuration.

The classical convex-linear homotopy that connects target with start system is

By choosing a random complex number 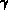, the regularity of the solution paths is guaranteed, see Figure 2. At t=0 we have the degenerate configuration which is trivial to solve.

  
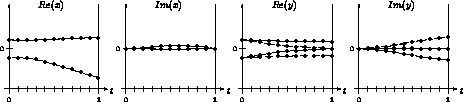
Figure 2: The different real and imaginary parts of x and y along the solution paths.

By following the solution paths defined by the homotopy we arrive for t = 1 at two real and two complex conjugated solutions of the target system. Note that in the x-component we have only two different paths.