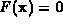
According to Bézout's theorem, the total degree bounds the number of isolated solutions. The total degree is defined as the product of the degrees of the polynomials in the system. By reduction we rewrite the system into an equivalent system with a lower total degree.
Linear reduction consists in the application of Gaussian elimination on the coefficient matrix, see [15, Chapter 7,]. We have extended this technique to nonlinear reduction. The idea is to replace a polynomial by an S-polynomial, as illustrated by the following example.
Consider the system 
displayed in (5).
The total degree of this system equals nine, but there are only two
finite solutions. The following reduction of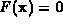 
is obtained by replacing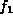 
by the S-polynomial 
,
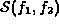computed as:
The total degree of the reduced system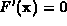 
equals six.
When the user chooses for nonlinear reduction, several bounds can be given to limit the complexity of the reduction algorithm. For instance, we have to restrict the number of replacements with equal total degree and must set a bound on the number of S-polynomials that may be computed.
Recently we have extended the reduction tool with two facilities
to deal with overdetermined systems.
The first one is described by Sommese and Wampler in [19].
Suppose we have a system of m equations in n unknowns, with m>n,
then we can generate a matrix with randomly chosen complex numbers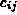 
to rewrite the system as follows
In [19], Sommese and Wampler prove that every isolated solution of the original system is an isolated solution of the constructed square system, with the corresponding multiplicity.
This method is recommended when the solution set of any choice of n equations from the system of m equations is unbounded. But often, it might happen that already the first choice of n equations has only isolated solutions and that the other equations are used to weed out this solution set. Then we would like to reduce these first n equations by using the remaining m-n equations. This mechanism is provided in the second facility, which uses R-polynomials to eliminate the leading monomials. Especially in view of handling sparse polynomial systems, this second type of reduction seems to be promising.
